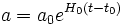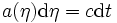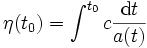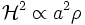Équation de Friedman

Équations de Friedmann

Le contenu de cet article du Portail:Cosmologie a fait l'objet d'une validation par un chercheur spécialiste du domaine le 18 juillet 2007 (comparer avec la version actuelle). Il est donc en principe exempt d'erreur grave. Ce label ne préjuge pas de la lisibilité de l'article ou de son accessibilité aux non spécialistes. Merci de bien vouloir passer par la page de discussion de l'article si vous trouvez l'article insuffisamment clair.

État d'avancement : Complet

Alexander Friedmann.

Les équations de Friedmann correspondent aux équations de la relativité générale (appelées équations d'Einstein) écrites dans le contexte d'un modèle cosmologique homogène et isotrope. Elles régissent donc l'évolution du taux d'expansion de l'univers et par suite de la distance entre deux astres lointains (le facteur d'échelle) et en fonction du temps appelé dans ce contexte temps cosmique. L'évolution de ces quantités est déterminée par les propriétés du contenu matériel de l'univers (rayonnement, atomes, matière noire, constante cosmologique, etc), ainsi éventuellement que la théorie de la gravitation considérée : il est en effet possible de remplacer la relativité générale par une autre théorie relativiste de la gravitation. Il peut par exemple s'agir d'une théorie tenseur-scalaire. Une autre façon de changer le modèle est de considérer la relativité générale standard mais dans un univers possédant une ou plusieurs dimensions supplémentaires. C'est le cas des modèles de cosmologie branaire^[1].

Les équations de Friedmann tirent leur nom du physicien russe Alexandre Friedmann qui a été le premier à les écrire dans le courant des années 1920, avec un premier article traitant des espaces à courbure spatiale positive en 1922, puis un plus général en 1924 incluant le cas d'une courbure spatiale négative. Il fut suivi de près par Georges Lemaître qui retrouva ces équations en 1927, prédisant ou expliquant la loi de Hubble avant que celle-ci ne soit découverte en 1929. Auparavant, en 1917, Albert Einstein les avait écrites dans le cas particulier d'un univers statique, ainsi que Willem de Sitter dans le cas d'un univers vide de matière, mais avec une constante cosmologique. Les équations de Friedmann sous leur forme actuelle ont été retrouvées et présentées sous une forme unifiée par Howard P. Robertson en 1929, puis indépendamment par Arthur G. Walker en 1936. Pour toutes ces raisons, le type de modèle cosmologique décrit par ces équations est appelé univers de Friedmann-Lemaître-Robertson-Walker (abrégé en FLRW). Le nom de Lemaître est souvent absent, ainsi plus rarement que celui de Friedmann, ces deux personnes étant néanmoins considérées comme les vrais découvreurs de ces équations.

Les équations de Friedmann sont à la base de la quasi totalité des modèles cosmologiques, dont bien sûr le Big Bang.

Sommaire

1 Les deux équations de Friedmann
2 Quelques solutions particulières
3 Solutions avec plusieurs espèces
- 3.1 Poussière et radiation
- 3.2 Poussière et constante cosmologique
4 Autres écritures
5 Interprétation
6 Dérivation des équations de Friedmann
7 Voir aussi
- 7.1 Liens internes
8 Références
- 8.1 Références générales actuelles
- 8.2 Articles historiques

Les deux équations de Friedmann

Il existe deux équations, la première reliant le taux d'expansion H, la courbure spatiale K et le facteur d'échelle a à la densité d'énergie ρ, la seconde reliant la pression P à la dérivée temporelle du taux d'expansion. La variable de temps utilisée est le temps cosmique, qui correspond essentiellement au temps mesuré sur Terre. Dans le cadre de la relativité générale, ces deux équations s'écrivent :

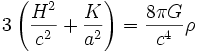$3 \left(\frac{H^2}{c^2} + \frac{K}{a^2} \right) = \frac{8 \pi G}{c^4} \rho$ ,

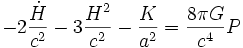$- 2 \frac{\dot H}{c^2} - 3 \frac{H^2}{c^2} - \frac{K}{a^2} = \frac{8 \pi G}{c^4} P$ ,

où G est la constante de Newton et c la vitesse de la lumière (la quantité $8π G / c 4$ est parfois appelée constante d'Einstein). Ces deux équations ne sont pas indépendantes : la seconde s'obtient en prenant la dérivée temporelle de la première, et en utilisant les équations de conservation, reliant la dérivée de la densité d'énergie à la pression. Quand on considère une extension de la relativité générale ou une autre théorie, ces équations sont modifiées. Pour cette raison, le terme d'équation de Friedmann est parfois employé au singulier, auquel cas la seule équation considérée est la première.

Il peut arriver (par exemple dans les modèles à dimensions supplémentaires) qu'elles ne soient plus conséquences l'une de l'autre. Dans les autres cas, il est possible de combiner les deux équations de façon à modifier la seconde, soit pour ne faire apparaître une certaine combinaison de la pression et de la densité d'énergie dans le membre de droite, soit pour ne faire apparaître que la dérivée seconde du facteur d'échelle dans le membre de gauche (voir paragraphe ci-dessous). Il est également possible d'effectuer un changement de variable pour utiliser le temps conforme plutôt que le temps cosmique. La résolution de ces équations s'effectue une fois la dépendance de la densité d'énergie et de la pression par rapport au temps ou au facteur d'échelle connus. Un certain nombre de solutions exactes sont connues.

Quelques solutions particulières

Quand le membre de droite ne comporte qu'une seule espèce, et en l'absence de courbure spatiale, les équations de Friedmann peuvent être résolues sans difficulté. En présence de plusieurs types de matière et/ou de courbure, des solutions analytiques exactes peuvent parfois être trouvées. Dans les autres cas, une résolution numérique des équations se fait sans difficulté.

Univers de poussière

Quand l'univers est empli de matière non relativiste (c'est-à-dire dont la pression est négligeable, d'où le terme de « poussière »), la densité d'énergie décroît uniquement du fait de la dilution due à l'expansion. Le facteur d'échelle évolue alors selon la loi

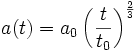$a(t) = a_0 \left(\frac{t}{t_0} \right)^\frac{2}{3}$ ,

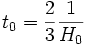les quantités a₀ et t₀ correspondant au facteur d'échelle et au temps évalués à une époque de référence donnée. De plus, l'âge de l'univers à cette époque, t₀ se déduit du taux d'expansion à la même époque par $t_0 = \frac{2}{3} \frac{1}{H_0}$ .

Démonstration

De fait de la nature de la matière, la densité d'énergie ρ_m évolue selon la loi

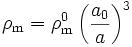$\rho_{\rm m} = \rho_{\rm m}^0 \left(\frac{a_0}{a}\right)^3$ ,

l'indice 0 se référant aux quantités correspondantes évaluée à une époque de référence donnée. On a ainsi, en l'absence de courbure

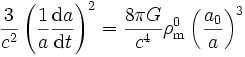$\frac{3}{c^2} \left(\frac{1}{a}\frac{{\rm d}a}{{\rm d}t}\right)^2 = \frac{8 \pi G}{c^4} \rho_{\rm m}^0 \left(\frac{a_0}{a}\right)^3$ .

On peut évaluer cette équation à une époque donnée, ce qui donne

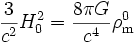$\frac{3}{c^2} H_0^2 = \frac{8 \pi G}{c^4}\rho_{\rm m}^0$ .

Si l'on note par x le « facteur d'échelle réduit », normalisé à 1 à l'époque de référence, la combinaison de ces deux équations peut s'écrire

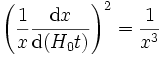$\left(\frac{1}{x}\frac{{\rm d}x}{{\rm d}(H_0 t)}\right)^2 = \frac{1}{x^3}$ .

La résolution de cette équation donne immédiatement

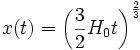$x(t) = \left(\frac{3}{2} H_0 t \right)^\frac{2}{3}$ .

Une telle solution est appelée, pour des raisons historiques univers d'Einstein-de Sitter, bien que ces derniers ne soient pas les premiers à avoir exhibé cette solution.

Dans un tel modèle, l'univers est donc plus jeune que le temps de Hubble. Si l'on prend la valeur mesurée de la constante de Hubble, à environ 70 kilomètres par seconde et par mégaparsec, l'application numérique donne un âge à peine supérieur à 9 milliards d'années. Cet âge étant significativement inférieur à l'âge estimé de nombreux objets astrophysiques (certaines étoiles, naines blanches, et la Voie lactée dans son ensemble), il est considéré qu'un tel univers de poussière ne peut correspondre à l'univers observable, ce qui est une des indications parmi d'autres de l'existence de l'énergie noire (voir ci-dessous). Il est aussi à noter que la dépendance du facteur d'échelle par rapport au temps est telle que sa dérivée seconde est négative, ce qui correspond à une phase d'expansion décélérée, compatible avec l'intuition que la nature attractive de la gravité a tendance à ralentir le mouvement d'expansion. Les observations, en particulier celle des supernovae de type Ia, suggèrent que la phase actuelle d'expansion est accélérée, ce qui est une autre indication de la nécessité de la présence d'énergie noire. Il est par contre certain que l'univers a connu par le passé une phase où son expansion était dominée par de la matière non relativiste, car c'est la seule époque où le mécanisme d'instabilité gravitationnelle peut se produire.

Univers de radiation

Quand l'univers est empli de matière relativiste ou de radiation, la densité d'énergie ρ_r décroît plus vite que précédemment car en plus de la dilution due à l'expansion, l'énergie des particules individuelles décroît avec l'expansion (ce n'est rien d'autre que l'effet de décalage vers le rouge). La densité décroissant plus vite, le taux d'expansion décroît également plus vite, et l'expansion décélère plus rapidement que dans le cas d'un univers de poussière. Le facteur d'échelle évolue selon la loi

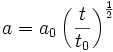$a = a_0 \left(\frac{t}{t_0} \right)^\frac{1}{2}$ .

L'âge de l'univers dans un tel modèle s'écrit alors

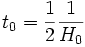$t_0 = \frac{1}{2} \frac{1}{H_0}$ .

Démonstration

De fait de la nature de la matière, la densité d'énergie ρ_r évolue désormais selon la loi

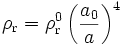$\rho_{\rm r} = \rho_{\rm r}^0 \left(\frac{a_0}{a}\right)^4$ ,

l'indice 0 se référant à nouveau aux quantités correspondantes évaluée à une époque de référence donnée. On a ainsi, en l'absence de courbure

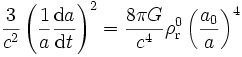$\frac{3}{c^2} \left(\frac{1}{a}\frac{{\rm d}a}{{\rm d}t}\right)^2 = \frac{8 \pi G}{c^4} \rho_{\rm r}^0 \left(\frac{a_0}{a}\right)^4$ .

On peut évaluer cette équation à une époque donnée, ce qui donne

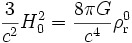$\frac{3}{c^2} H_0^2 = \frac{8 \pi G}{c^4}\rho_{\rm r}^0$ .

Si l'on note par x le « facteur d'échelle réduit », normalisé à 1 à l'époque de référence, la combinaison de ces deux équations peut s'écrire

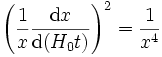$\left(\frac{1}{x}\frac{{\rm d}x}{{\rm d}(H_0 t)}\right)^2 = \frac{1}{x^4}$ .

La résolution de cette équation donne immédiatement

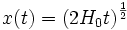$x(t) = \left(2 H_0 t \right)^\frac{1}{2}$ .

Comme dans le cas de l'univers de poussière, l'expansion est décélérée et l'âge donné par ce modèle ne peut correspondre aux observations. Ce modèle correspond par contre bien aux époques reculées de l'histoire de l'univers, quand la quasi-totalité de la matière était sous forme relativiste. En particulier l'époque de la nucléosynthèse s'est produite quand la densité d'énergie était majoritairement due à de la matière relativiste, hypothèse que l'on teste directement par la mesure de l'abondance des éléments légers. D'autres indications du fait que l'univers a connu une période dominée par la radiation est l'existence du fond diffus cosmologique.

Constante cosmologique

Une constante cosmologique peut s'interpréter comme une forme de matière de densité d'énergie constante et de pression exactement opposée à celle-ci. Quand la densité d'énergie est positive, les équations de Friedmann admettent, en l'absence de courbure spatiale, la solution exponentielle

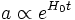$a \propto e^{H_0 t}$ ,

le paramètre de Hubble étant constant au cours du temps.

Démonstration

La première équation de Friedmann donne comme d'habitude

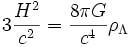$3 \frac{H^2}{c^2} = \frac{8 \pi G}{c^4} \rho_\Lambda$ ,

la densité d'énergie de la constante cosmogique étant ici constante. Le paramètre de Hubble est donc constant, et l'on a donc

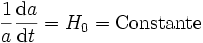$\frac{1}{a}\frac{{\rm d}a}{{\rm d} t} = H_0 = {\rm Constante}$ ,

dont la solution est de façon évidente

$a = a_0 e^{H_0 (t - t_0)}$

Un tel modèle représente un univers éternel, sans commencement ni fin. C'est l'univers de de Sitter, obéissant au principe cosmologique parfait. Il existe une autre configuration donnant lieu à la même dynamique de l'expansion : les deux formes de matière sont alors de la matière ordinaire non relativiste, et une forme de matière extrêmement exotique, appelée champ C, responsable d'une création continue de matière compensant exactement la dilution due à l'expansion. C'est la base de la théorie de l'état stationnaire, aujourd'hui abandonnée en raison de l'absence totale de motivation théorique ou observationnelle du champ C. Enfin, en présence d'un champ scalaire, celui-ci peut, temporairement se comporter de façon extrêmement semblable à une constante cosmologique, comportement qu'il peut par la suite abandonner. Ainsi, il est possible que sous l'effet d'un tel champ scalaire, l'expansion de l'univers connaisse une phase exponentielle. C'est la base des modèles d'inflation cosmique qui prédisent l'existence d'une telle phase à une époque très reculée de l'histoire de l'univers.

Équation d'état constante

Tant que la pression est proportionnelle à la densité, avec une constante de proportionnalité constante, on peut résoudre les équations de Friedmann. On note w le rapport de la pression à la densité,

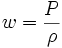$w = \frac{P}{\rho}$ .

Pour toute forme de matière raisonnable, le facteur w est compris entre -1 et 1. Le cas où w est inférieur à -1 correspond à ce qui est appelé énergie fantôme, une forme d'énergie extrêmement spéculative donnant lieu à un scénario cosmologique étrange, le Big Rip. Les cas où w vaut 0, 1/3, -1 correspondent respectivement aux cas de la poussière, la radiation et de la constante cosmologique. Quand w est différent de -1, on obtient

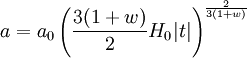$a = a_0 \left(\frac{3 (1 + w)}{2} H_0 |t| \right)^\frac{2}{3(1 + w)}$ .

Démonstration

Par les équations de conservation, l'évolution temporelle de la densité d'énergie est déterminée par

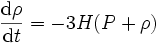$\frac{{\rm d}\rho}{{\rm d}t} = - 3 H (P + \rho)$ .

En utilisant la relation entre densité d'énergie et pression et la définition de la constante de Hubble, cette équation se réécrit

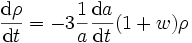$\frac{{\rm d}\rho}{{\rm d}t} = - 3 \frac{1}{a}\frac{{\rm d}a}{{\rm d}t} (1 + w) \rho$ ,

soit

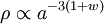$\rho \propto a^{-3(1+w)}$ .

Les équations de Friedmann se réécrivent alors

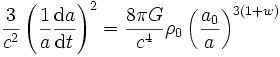$\frac{3}{c^2} \left(\frac{1}{a}\frac{{\rm d}a}{{\rm d}t}\right)^2 = \frac{8 \pi G}{c^4} \rho_0 \left(\frac{a_0}{a}\right)^{3(1+w)}$ .

On peut évaluer cette équation à une époque donnée, ce qui donne

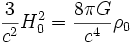$\frac{3}{c^2} H_0^2 = \frac{8 \pi G}{c^4}\rho_0$ .

Si l'on note par x le « facteur d'échelle réduit », normalisé à 1 à l'époque de référence, la combinaison de ces deux équations peut s'écrire

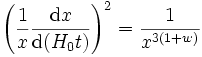$\left(\frac{1}{x}\frac{{\rm d}x}{{\rm d}(H_0 t)}\right)^2 = \frac{1}{x^{3(1+w)}}$ .

Quand w = -1, on est dans le cas d'une constante cosmologique vu précédemment. Dans les autres cas, la résolution de cette équation donne immédiatement

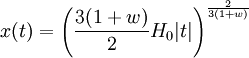$x(t) = \left(\frac{3(1+w)}{2} H_0 |t| \right)^\frac{2}{3(1+w)}$ .

Quand w est supérieur à -1, le facteur d'échelle tend vers 0 quand t tend vers 0. Il y a donc un Big Bang, et l'expansion se poursuit indéfiniment. À l'inverse, quand w est inférieur à -1, alors cette fois, le facteur d'échelle tend vers 0 quand t est négatif et tend vers l'infini, et il tend vers l'infini quand t tend vers 0. Dans ce cas, on a un univers existant de toute éternité, mais ayant une durée de vie finie dans le futur (voir ci-dessous).

Quand w est supérieur à -1, l'âge de l'univers s'écrit

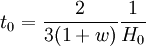$t_0 = \frac{2}{3(1+w)} \frac{1}{H_0}$ .

Les valeur de w égales à 0 et 1/3 redonnent bien sûr les résultats précédents. Quand w est égal à -1, on a un univers sans commencement ni fin, et ne présentant pas d'évolution. Quand w est inférieur à -1, on a un univers sans commencement, mais atteignant une singularité gravitationnelle dans un temps fini, bien que restant toujours en expansion. En effet, quand le facteur d'échelle tend vers l'infini, alors la densité d'énergie diverge, et ce en un temps fini : c'est le Big Rip (litt. « grande déchirure »). Le temps qu'il reste à l'univers avant cette singularité est donné par

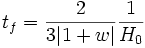$t_f = \frac{2}{3|1+w|} \frac{1}{H_0}$ .

Solutions avec plusieurs espèces

Dans le cas où plusieurs espèces ou formes de matière emplissent l'univers et participent notablement aux équations de Friedmann, il faut tenir compte de leurs équations d'état respective et de leur abondance relative. Dans le cas de deux espèces, par exemple, la première équation de Friedmann se réécrit

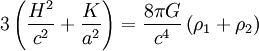$3 \left(\frac{H^2}{c^2} + \frac{K}{a^2} \right) = \frac{8 \pi G}{c^4} \left(\rho_1 + \rho_2\right)$ .

Si l'on appelle w₁ et w₂ les rapports de la pression à la densité d'énergie de chacune des deux espèces et qu'on les suppose constants au court du temps, on peut réécrire cette équation à l'aide de diverses variables adimensionnées, sous la forme

$\left(\frac{{\rm{d}}x}{x H_0 {\rm{d}} t}\right)^2 = \left[\Omega^0_1 x^{-3(1 + w_1)}+ \Omega_2^0 x^{-3(1 + w_2)}\right]$ ,

où l'on a défini, à partir d'un époque de référence notée avec l'indice ou l'exposant 0 la densité critique 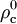$\rho^0_{\rm{c}}$ par

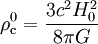$\rho^0_{\rm{c}} = \frac{3 c^2 H^2_0}{8 \pi G}$ ,

ainsi que les quantités sans dimension appelées paramètres de densité 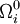$\Omega_i^0$ par

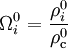$\Omega_i^0 = \frac{\rho_i^0}{\rho_{\rm{c}}^0}$ ,

et le facteur d'échelle normalisé, x, par $x = a / a 0$ .

Démonstration

En prenant une époque de référence, que l'on note avec l'indice ou l'exposant 0, on a

$3 \left(\frac{H^2}{c^2} + \frac{K}{a^2} \right) = \frac{8 \pi G}{c^4} \left[\rho^0_1 \left(\frac{a_0}{a}\right)^{3(1 + w_1)}+ \rho_2^0 \left(\frac{a_0}{a}\right)^{3(1 + w_2)}\right]$ .

On introduit la densité critique 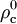$\rho^0_{\rm{c}}$ par

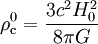$\rho^0_{\rm{c}} = \frac{3 c^2 H^2_0}{8 \pi G}$ ,

ainsi que les quantités sans dimension appelées paramètres de densité 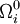$\Omega_i^0$ par

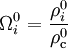$\Omega_i^0 = \frac{\rho_i^0}{\rho_{\rm{c}}^0}$ .

Ainsi, on obtient, en introduisant le facteur d'échelle normalisé $x = a / a 0$ ,

$\frac{H^2}{H_0^2} + \frac{K c^2}{H_0^2 a_0^2} \frac{1}{x^2} = \left[\Omega^0_1 x^{-3(1 + w_1)}+ \Omega_2^0 x^{-3(1 + w_2)}\right]$ .

En évaluant cette quantité à l'époque de référence, il vient alors

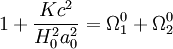$1 + \frac{K c^2}{H_0^2 a_0^2} = \Omega^0_1 + \Omega_2^0$ ,

d'où finalement

$\left(\frac{{\rm{d}}x}{x H_0 {\rm{d}} t}\right)^2 + \left(\Omega^0_1 + \Omega_2^0 - 1\right)\frac{1}{x^2} = \left[\Omega^0_1 x^{-3(1 + w_1)}+ \Omega_2^0 x^{-3(1 + w_2)}\right]$ .

Cette expression se simplifie quand la densité totale égale la densité critique, ou, de façon équivalente quand la somme des paramètres de densité vaut 1. On a alors

$\left(\frac{{\rm{d}}x}{x H_0 {\rm{d}} t}\right)^2 = \left[\Omega^0_1 x^{-3(1 + w_1)}+ \Omega_2^0 x^{-3(1 + w_2)}\right]$ .

Chacune de ces deux expressions se généralise à un nombre arbitraire de composantes. Des solutions exactes existent pour certaines valeurs des paramètres w₁ et w₂.

En particulier, dans le cadre du modèle standard de la cosmologie, l'univers peut être décrit comme étant rempli de trois types d'espèce : de la matière relativiste (neutrinos et rayonnement), de la matière non relativiste (matière baryonique et matière noire), et de l'énergie noire, que l'on va ici approximer par une constante cosmologique. Les abondances relatives de ces espèces, qui varient avec le temps font qu'il n'arrive jamais qu'elles coexistent avec chacune des densités d'énergie significatives. À l'époque actuelle, on trouve essentiellement de l'énergie noire et de la matière non relativiste, alors qu'aux époques reculées, on trouvait de la matière relativiste et non relativiste, la constante cosmologique étant négligeable. Ceci vient du fait que les abondances de ces différents types de matière varient au cours du temps selon $1 / x 3(1 + w)$ : la densité d'énergie associée à la constante cosmologique reste constante, alors que celle de la matière relativiste ou non relativiste croît à mesure que l'on remonte vers le passé.

Poussière et radiation

Quand on remonte vers le passé, les densités de matière non relativiste (« poussière ») ou relativiste (« radiation ») croissent comme $x - 3$ et $x - 4$ respectivement. On a donc

$\left(\frac{{\rm{d}}x}{x H_0 {\rm{d}} t}\right)^2 = \left[\frac{\Omega^0_{\rm{m}}}{x^3} + \frac{\Omega^0_{\rm{r}}}{x^4}\right]$ ,

avec

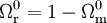$\Omega^0_{\rm{r}} = 1 - \Omega^0_{\rm{m}}$ .

L'intégration donne

$\frac{4 \left(1 - \Omega^0_{\rm{m}}\right)^\frac{3}{2}}{3\left(\Omega^0_{\rm{m}}\right)^2} \left[1 - \sqrt{1 + \frac{\Omega^0_{\rm{m}} x}{1 - \Omega^0_{\rm{m}}}}\left(1 - \frac{1}{2}\frac{\Omega^0_{\rm{m}} x}{1 - \Omega^0_{\rm{m}}}\right)\right] = H_0 t$ .

Démonstration

On simplifie l'équation de départ en

$\left(\frac{x {\rm{d}}x}{H_0 {\rm{d}} t}\right)^2 = \left[\Omega^0_{\rm{m}} x + 1 - \Omega^0_{\rm{m}}\right]$ ,

soit

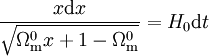$\frac{x {\rm{d}}x}{\sqrt{\Omega^0_{\rm{m}} x + 1 - \Omega^0_{\rm{m}}}} = H_0 {\rm{d}} t$ .

On effectue le changement de variable

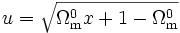$u = \sqrt{\Omega^0_{\rm{m}} x + 1 - \Omega^0_{\rm{m}}}$ ,

dont on tire

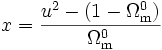$x = \frac{u^2 - \left(1 - \Omega^0_{\rm{m}}\right)}{\Omega^0_{\rm{m}}}$ ,

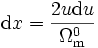${\rm{d}} x = \frac{2 u {\rm{d}} u}{\Omega^0_{\rm{m}}}$ .

L'équation à résoudre devient

$\frac{2 \left[u^2 - \left(1 - \Omega^0_{\rm{m}}\right)\right]{\rm{d}} u}{\left(\Omega^0_{\rm{m}}\right)^2} = H_0 {\rm{d}} t$ ,

qui s'intègre immédiatement en

$\frac{2}{\left(\Omega^0_{\rm{m}}\right)^2} \left[\frac{u^3}{3} - \left(1 - \Omega^0_{\rm{m}}\right) u\right]^u_{u_i} = H_0 t$ ,

la quantité $u i$ correspondant à la valeur $x = 0$ , soit 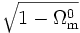$\sqrt{1 - \Omega^0_{\rm{m}}}$ . On trouve alors

$\frac{2}{\left(\Omega^0_{\rm{m}}\right)^2} \left[\sqrt{\Omega^0_{\rm{m}} x + 1 - \Omega^0_{\rm{m}}} \left( \frac{\Omega^0_{\rm{m}} x + 1 - \Omega^0_{\rm{m}}}{3} - \left(1 - \Omega^0_{\rm{m}}\right)\right) + \frac{2}{3} \left(1 - \Omega^0_{\rm{m}}\right)^\frac{3}{2} \right] = H_0 t$ ,

soit

Selon la valeur de x par rapport à 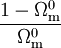$\frac{1 - \Omega^0_{\rm{m}}}{\Omega^0_{\rm{m}}}$ , qui correspond à l'époque de transition où densité de matière relativiste et non relativiste sont égales, on retrouve deux régimes précédemment étudiés. Pour les valeurs de x petites, on obtient

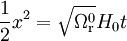$\frac{1}{2} x^2 = \sqrt{{\Omega^0_{\rm{r}}}}H_0 t$ ,

ce qui correspond au résultat pour l'univers de radiation trouvé ci-dessus, la valeur de $H 0$ étant remplacée par 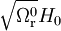$\sqrt{{\Omega^0_{\rm{r}}}}H_0$ , correspond à la valeur qu'aurait la constante de Hubble en l'absence de matière non relativiste.

Dans l'autre régime, on trouve

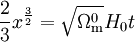$\frac{2}{3} x^\frac{3}{2} = \sqrt{{\Omega^0_{\rm{m}}}}H_0 t$ ,

qui là encore redonne le résultat de l'univers de poussière à la correction sur la valeur de la constante de Hubble près.

Poussière et constante cosmologique

Les seconds cas particuliers importants sont celui d'un univers dominé par de la matière non relativiste (w_m = 0) et dont la constante cosmologique (w_Λ = -1) devient dominante. C'est selon toute vraisemblance dans une situation similaire que se trouve notre univers, l'accélération de l'expansion de l'univers attestant de l'existence d'une forme de matière se comportant de façon assez voisine à une constante cosmologique. 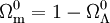Dans ce cas, l'intégration des équations de Friedmann donne, avec $\Omega_{\rm{m}}^0 = 1 - \Omega_\Lambda^0$ ,

$\frac{a}{a_0} = \left[\sqrt{\frac{1 - \Omega_\Lambda^0}{\Omega_\Lambda^0}} \sinh\left(\frac{3 \sqrt{\Omega_\Lambda^0}}{2} H_0 t\right) \right]^\frac{2}{3}$ .

Démonstration

On reprend à nouveau la même équation avec les variables réduites. Dans un univers spatialement plat, on a

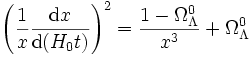$\left(\frac{1}{x}\frac{{\rm d}x}{{\rm d}(H_0 t)}\right)^2 = \frac{1 - \Omega_\Lambda^0}{x^3} + \Omega_\Lambda^0$ ,

que l'on peut réécrire en

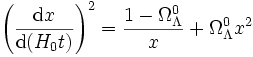$\left(\frac{{\rm d}x}{{\rm d}(H_0 t)}\right)^2 = \frac{1 - \Omega_\Lambda^0}{x} + \Omega_\Lambda^0 x^2$ ,

soit

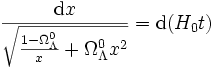$\frac{{\rm d}x}{\sqrt{\frac{1 - \Omega_\Lambda^0}{x} + \Omega_\Lambda^0 x^2}} = {\rm d}(H_0 t)$ ,

ou bien

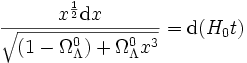$\frac{x^\frac{1}{2}{\rm d}x}{\sqrt{(1 - \Omega_\Lambda^0) + \Omega_\Lambda^0 x^3}} = {\rm d}(H_0 t)$ .

On pose

y = H 0 t

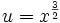$u = x^\frac{3}{2}$ ,

ce qui permet de réécrire l'équation précédente en

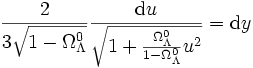$\frac{2}{3 \sqrt{1 - \Omega_\Lambda^0}}\frac{{\rm d}u}{\sqrt{1 + \frac{\Omega_\Lambda^0}{1 - \Omega_\Lambda^0} u^2}} = {\rm d}y$ .

En posant

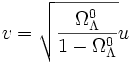$v = \sqrt{\frac{\Omega_\Lambda^0}{1 - \Omega_\Lambda^0}} u$ ,

d'où

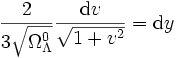$\frac{2}{3 \sqrt{\Omega_\Lambda^0}}\frac{{\rm d}v}{\sqrt{1 + v^2}} = {\rm d}y$ .

Cette équation peut s'intégrer en

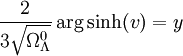$\frac{2}{3 \sqrt{\Omega_\Lambda^0}} \arg\sinh(v) = y$ ,

que l'on inverse en

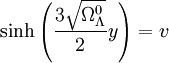$\sinh\left(\frac{3 \sqrt{\Omega_\Lambda^0}}{2} y\right) = v$ ,

soit

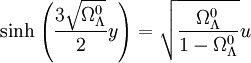$\sinh\left(\frac{3 \sqrt{\Omega_\Lambda^0}}{2} y\right) = \sqrt{\frac{\Omega_\Lambda^0}{1 - \Omega_\Lambda^0}} u$ ,

et finalement

$\frac{a}{a_0} = \left[\sqrt{\frac{1 - \Omega_\Lambda^0}{\Omega_\Lambda^0}} \sinh\left(\frac{3 \sqrt{\Omega_\Lambda^0}}{2} H_0 t\right) \right]^\frac{2}{3}$ .

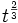Pour les temps petits, on peut effectuer un développement limité qui redonne le comportement en $t^\frac{2}{3}$ :

$\frac{a}{a_0} \sim \left[\frac{3}{2} \sqrt{\Omega_{\rm{m}}^0} H_0 t \right]^\frac{2}{3}$ .

On retrouve exactement la formule déjà obtenue pour un univers de poussière, à ceci près que c'est 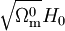$\sqrt{\Omega_{\rm{m}}^0} H_0$ qui apparaît au lieu de $H 0$ . Ceci provient du fait qu'en l'absence de constante cosmologique, la constante de Hubble serait réduite d'un facteur 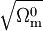$\sqrt{\Omega_{\rm{m}}^0}$ . Le fait que l'on retrouve la formule de l'univers de poussière provient du fait qu'à ces époques, la constante cosmologique est négligeable par rapport à la densité de matière.

À l'inverse, pour les temps grands, on retrouve le comportement exponentiel du facteur d'échelle par rapport au temps :

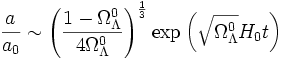$\frac{a}{a_0} \sim \left(\frac{1 - \Omega_\Lambda^0}{4 \Omega_\Lambda^0}\right)^\frac{1}{3} \exp\left(\sqrt{\Omega_\Lambda^0} H_0 t\right)$ .

Dans ce cas, la constante de Hubble tend effectivement vers la valeur asymptotique 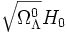$\sqrt{\Omega_\Lambda^0} H_0$ qui entre dans l'exposant. La transition entre ces deux régimes s'effectue au moment où l'argument du sinus hyperbolique est de l'ordre de 1. Quand cela se produit, la quantité $a / a 0$ est de l'ordre de $\left[\left(1 - \Omega_\Lambda^0\right) / \Omega_\Lambda^0 \right]^\frac{1}{3}$ . Cela correspond au moment où la densité d'énergie associée à la constante cosmologique devient de l'ordre de celle de la matière. Avant cette époque c'est celle de la matière qui domine, et l'on retrouve les résultats de l'univers de poussière, après cette époque, c'est la constante cosmologique qui domine, et l'on retrouve la dynamique de l'univers de de Sitter.

Un point intéressant est de calculer la relation entre âge de l'univers et temps de Hubble $1 / H 0$ . On trouve ainsi

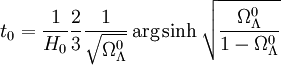$t_0 = \frac{1}{H_0}\frac{2}{3} \frac{1}{\sqrt{\Omega_\Lambda^0}} \arg\sinh\sqrt{\frac{\Omega_\Lambda^0}{1 - \Omega_\Lambda^0}}$ .

Pour des valeurs petites de 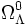$\Omega_\Lambda^0$ , on retrouve la valeur habituelle de $t 0 = 2 / 3 H 0$ , alors qu'à mesure que 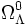$\Omega_\Lambda^0$ croît (en restant bien sûr inférieur à 1), l'âge de l'univers devient plus grand que le temps de Hubble.

Autres écritures

Dans certains cas, on peut préférer exprimer les équations en fonction du facteur d'échelle et non du paramètre de Hubble. Il vient alors

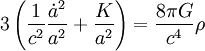$3 \left(\frac{1}{c^2}\frac{\dot a^2}{a^2} + \frac{K}{a^2} \right) = \frac{8 \pi G}{c^4} \rho$ ,

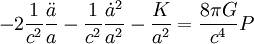$- 2 \frac{1}{c^2}\frac{\ddot a}{a} - \frac{1}{c^2}\frac{\dot a^2}{a^2} - \frac{K}{a^2} = \frac{8 \pi G}{c^4} P$ .

Le cas échéant, la seconde équation peut se réécrire en faisant disparaître le terme de courbure en utilisant la première, ce qui donne

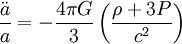$\frac{\ddot a}{a} = - \frac{4 \pi G}{3} \left(\frac{\rho + 3 P}{c^2}\right)$ .

Cette dernière forme, qui donne l'accélération relative de deux objets distants du fait de l'expansion de l'univers est un cas particulier de l'équation de Raychaudhuri et pour cette raison parfois appelée ainsi. Plus généralement, toute écriture de la seconde équation de Friedmann faisant apparaître la dérivée seconde du facteur d'échelle (ou la dérivée première du taux d'expansion) peut être appelée ainsi.

Enfin, l'on peut également préférer extraire la constante cosmologique du contenu matériel de l'univers, lui donnant ainsi un rôle purement géométrique. Ce choix est aujourd'hui considéré comme peu opportun en cosmologie car la nature exacte de l'énergie noire est inconnue, mais correspond historiquement à celui d'Einstein et de Lemaître. On obtient alors, en considérant que la constante cosmologique est homogène à l'inverse du carré d'une longueur,

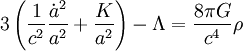$3 \left(\frac{1}{c^2}\frac{\dot a^2}{a^2} + \frac{K}{a^2} \right) - \Lambda = \frac{8 \pi G}{c^4} \rho$ ,

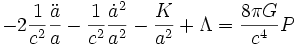$- 2 \frac{1}{c^2}\frac{\ddot a}{a} - \frac{1}{c^2}\frac{\dot a^2}{a^2} - \frac{K}{a^2} + \Lambda = \frac{8 \pi G}{c^4} P$ .

Les écritures ci-dessus utilisent le temps cosmique. Il est possible et parfois utile de lui substituer le temps conforme, η, défini par la formule

$a(\eta) {\rm d} \eta = c {\rm d} t\,$

ou encore

$\eta(t_0)=\int^{t_0}c\frac{{\rm d}t}{a(t)}$

de sorte que l'élément de longueur devienne proportionnel à une métrique de Minkowski (on dit conformément minkowskien) :

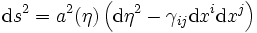${\rm d}s^2 = a^2(\eta) \left({\rm d}\eta^2 - \gamma_{ij} {\rm d}x^i {\rm d}x^j\right)$ .

Dans ce cas, on peut définir un « paramètre de Hubble conforme » 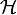${\mathcal H}$ par

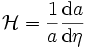${\mathcal H} = \frac{1}{a}\frac{{\rm d}a}{{\rm d}\eta}$ .

Une telle quantité n'a pas d'interprétation physique immédiate, mais permet la réécriture des équations de Friedmann en terme du temps conforme :

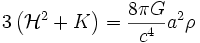$3 \left({\mathcal H}^2 + K \right) = \frac{8 \pi G}{c^4} a^2 \rho$ ,

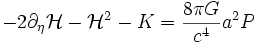$- 2 \partial_\eta {\mathcal H} - {\mathcal H}^2 - K = \frac{8 \pi G}{c^4} a^2 P$ .

La résolution de ces équations suit sensiblement les mêmes étapes que dans les cas précédents. En particulier, on trouve les dépendances suivantes du facteur d'échelle par rapport au temps conforme :

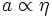$a \propto \eta$ dans un univers de radiation
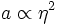$a \propto \eta^2$ dans un univers de poussière
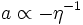$a \propto - \eta^{-1}$ avec une constante cosmologique
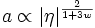$a \propto |\eta|^\frac{2}{1 + 3 w}$ avec une forme de matière dont l'équation d'état est $P = w ρ$ .

Démonstration

La relation

${\mathcal H}^2 \propto a^2 \rho$

a pour conséquence immédiate que

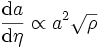$\frac{{\rm d}a}{{\rm d}\eta} \propto a^2 \sqrt{\rho}$ .

En utilisant de plus le fait que pour une équation d'état du type $P = w ρ$ , la dépendance de ρ reste

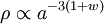$\rho \propto a^{-3(1+w)}$ ,

il vient

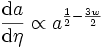$\frac{{\rm d}a}{{\rm d}\eta} \propto a^{\frac{1}{2}-\frac{3w}{2}}$ ,

qui se résout en

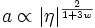$a \propto |\eta|^{\frac{2}{1+3w}}$ .

À noter que η varie de 0 à $+\infty$ selon une loi de puissance avec exposant positif tant que w est supérieur à -1/3, varie exponentiellement quand w vaut -1/3 et varie de $-\infty$ à 0 selon une loi de puissance avec exposant négatif quand w est inférieur à -1/3.

L'intérêt de résoudre les équations de Friedmann en terme du temps conforme vient du fait que le concept d'horizon des particules et d'horizon des événements est très étroitement relié à la relation $a (η)$ , et notamment à son comportement pour les plus petites et plus grandes valeurs de η. De plus, les concepts de distance angulaire et de distance de luminosité dépendent eux aussi directement de cette même relation.

Interprétation

Les équations de Friedmann en présence de matière non relativiste peuvent se retrouver (de façon heuristique) par un raisonnement purement newtonien. On peut en effet considérer l'évolution d'une sphère de matière, dont on suppose la densité constante à tout instant. Cette hypothèse est inexacte en général, mais la faire permet de se placer dans une situation assez semblable à celle d'un univers homogène et isotrope. auquel cas, le taux d'expansion de la sphère est relié à sa densité par la même formule que la première équation de Friedmann.

Démonstration

On considère donc une sphère de poussière (c'est-à-dire que l'on néglige les forces de pression) de masse M dont on étudie l'évolution du rayon R(t) en fonction du temps, sous l'effet de la gravité. Un point situé à la surface de la sphère est uniquement soumis aux forces de gravité, et obéit donc à l'équation

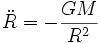$\ddot R = - \frac{G M}{R^2}$ .

En multipliant par la dérivée de R, il vient

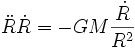$\ddot R \dot R = - G M \frac{\dot R}{R^2}$ .

Les deux membres de l'équation correspondent à des dérivées par rapport au temps, que l'on peut intégrer en

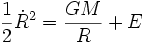$\frac{1}{2} \dot R^2 = \frac{G M}{R} + E$ ,

la quantité E étant alors une constante d'intégration déterminée par les conditions initiales. Cette constante d'intégration n'est rien d'autre que l'énergie totale par unité de masse, égale à la somme de l'énergie cinétique et de l'énergie potentielle :

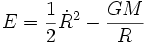$E = \frac{1}{2} \dot R^2 - \frac{GM}{R}$ .

Si l'on remplace la masse de la sphère par le produit de son volume et de sa densité &\mu;, on obtient

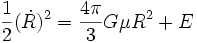$\frac{1}{2} (\dot R)^2 = \frac{4 \pi}{3} G \mu R^2 + E$ ,

que l'on peut réécrire en

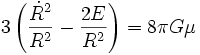$3 \left(\frac{\dot R^2}{R^2} - \frac{2 E}{R^2} \right) = 8 \pi G \mu$ .

Enfin, en remplaçant la densité de masse μ par la densité d'énergie de masse ρ = μ c², on trouve

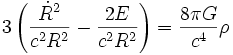$3 \left(\frac{\dot R^2}{c^2 R^2} - \frac{2 E}{c^2 R^2} \right) = \frac{8 \pi G}{c^4} \rho$ .

La différence cruciale entre ces deux approches vient du rôle joué par la courbure K (dans le modèle relativiste) qui s'apparente dans le modèle newtonien à une constante d'intégration sans signification géométrique. En relativité générale elle détermine les propriétés géométriques de l'espace.

Dérivation des équations de Friedmann

Les équations de Friedmann ne sont rien d'autre que l'écriture des équations d'Einstein décrivant un univers homogène et isotrope. Leur dérivation ne pose pas de difficulté particulière, et elles représentent même une des solutions analytiques exactes les plus simples parmi celles connues à ces équations.

Démonstration

L'hypothèse de l'homogénéité et de l'isotropie des sections spatiales de l'univers permet d'écrire l'élément de longueur sous la forme

d s 2 = c 2 d t 2 - a 2 (t)γ i j d x i d x j

où γ_ij représente la métrique des sections spatiales, décrites par les coordonnées xⁱ. Un tel système de coordonnées est appelé coordonnées comobiles. Un observateur décrivant la trajectoire $x i = Constante$ suit une géodésique. Il est appelé observateur fondamental. Son temps propre correspond ici exactement à la coordonnée t, appelée temps cosmique (le temps propre des observateurs fondamentaux). Une telle trajectoire correspond en première approximation aux trajectoires des galaxies, si l'on fait abstraction de leur mouvement propre. La distance entre deux observateurs fondamentaux augmente proportionnellement à la fonction a(t), qui est le facteur d'échelle. Une fois cette forme de la métrique supposée, les équations d'Einstein déterminent l'évolution temporelle du facteur d'échelle.

Les coefficients de la métrique s'écrivent

g 00 = c 2

g 0 i = 0

g i j = - a 2 (t)γ i j

La forme exacte de $γ i j$ importe peu et dépend du type de coordonnées choisi (cartésiennes ou sphériques, par exemple, si on suppose les sections spatiales euclidiennes). Le seul résultat important est de savoir que les sections spatiales étant homogènes et isotropes forment un espace à symétrie maximale, et qu'un tel espace dont la métrique serait $γ i j$ a un tenseur de Ricci donné par

3 R i j = 2 K γ i j

la quantité K étant la courbure spatiale associée.

L'inverse de la métrique a pour coordonnées :

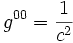$g^{00} = \frac{1}{c^2}$ ,

g 0 i = 0

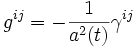$g^{ij} = - \frac{1}{a^2(t)} \gamma^{ij}$ ,

où $γ i j$ représente la métrique inverse de $γ i j$ .

Les symboles de Christoffel s'écrivent :

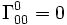$\Gamma^0_{00} = 0$ ,

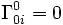$\Gamma^0_{0i} = 0$ ,

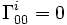$\Gamma^i_{00} = 0$ ,

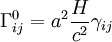$\Gamma^0_{ij} = a^2 \frac{H}{c^2}\gamma_{ij}$ ,

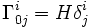$\Gamma^i_{0j} = H \delta^i_j$ ,

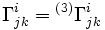$\Gamma^i_{jk} = {}^{(3)} \Gamma^i_{jk}$ ,

où H est le paramètre de Hubble, donne par $H = d a / a d t$ , et 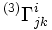${}^{(3)} \Gamma^i_{jk}$ correspond aux symboles de Christoffel associés à la métrique $γ i j$ .

Les coefficients du tenseur de Ricci s'écrivent alors

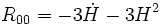$R_{00} = - 3 \dot H - 3 H^2$ ,

R 0 i = 0

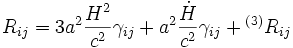$R_{ij} = 3 a^2 \frac{H^2}{c^2}\gamma_{ij} + a^2 \frac{\dot H}{c^2} \gamma_{ij} + {}^{(3)}R_{ij}$ ,

La courbure scalaire s'écrit

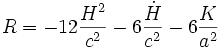$R = - 12 \frac{H^2}{c^2} - 6 \frac{\dot H}{c^2} - 6 \frac{K}{a^2}$ .

Le tenseur d'Einstein s'écrit enfin

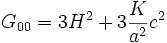$G_{00} = 3 H^2 + 3 \frac{K}{a^2}{c^2}$ ,

G 0 i = 0

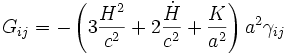
$G_{ij} = - \left(3 \frac{H^2}{c^2} + 2 \frac{\dot H}{c^2} + \frac{K}{a^2} \right) a^2 \gamma_{ij}$

Il faut maintenant déterminer le tenseur énergie-impulsion de la matière. Le seul tenseur énergie-impulsion compatible avec les hypothèses d'homogénéité et d'isotropie utilisées est celui d'un fluide parfait. Il est alors uniquement décrit par la densité d'énergie, la pression et la quadrivitesse du fluide selon la formule

T μν = (P + ρ) u μ u ν - P g μν

Cette quadrivitesse correspond à celle des observateurs fondamentaux. La formule donnant la quadrivitesse étant

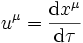$u^\mu = \frac{{\rm d}x^\mu}{{\rm d}\tau}$ ,

et le temps propre étant donné par le temps coordonné, on a immédiatement

u 0 = 1

u i = 0

et les composantes contravariantes s'écrivent

u 0 = c 2

u i = 0

Les composantes du tenseur énergie-impulsion sont donc

T 00 = ρ c 2

T 0 i = 0

T i j = P a 2 γ i j

En utilisant la formule des équations d'Einstein, la composante 00 donne donc

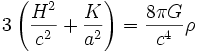$3 \left(\frac{H^2}{c^2} + \frac{K}{a^2}\right) = \frac{8 \pi G}{c^4} \rho$ ,

et la composante ij donne

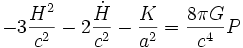$- 3 \frac{H^2}{c^2} - 2 \frac{\dot H}{c^2} - \frac{K}{a^2} = \frac{8 \pi G}{c^4} P$ .

Voir aussi

Liens internes

Références

↑ Ces modèles sont motivés par la théorie des cordes, tout en en étant logiquement indépendants, dans laquelle des dimensions supplémentaires apparaissent naturellement.

Références générales actuelles

Ouvrages spécialisés sur la cosmologie.
(en) Charles W. Misner, Kip S. Thorne & John Archibald Wheeler, Gravitation, W. H. Freeman, New York, 1973, 1280 pages (ISBN 0716703440), chapitre 27.
Jean-Pierre Luminet, L'invention du Big Bang, Seuil, coll. « Points Sciences » (2004) (ISBN 2020611481)

Articles historiques

(de) Albert Einstein, Kosmologische Betrachtungen zur allgemeinen Relativitätstheorie, Preussische Akademie der Wissenschaften, Sitzungsberichte, p. 142-152 (1917). Sur l'univers d'Einstein.
(en) Willem de Sitter, Einstein's theory of gravitation and its astronomical consequences. Third paper, Monthly Notices of the Royal Astronomical Society 78, 3-28 (1917). Introduit l'univers de de Sitter.
(de) Alexandre Friedmann Über die Krümmung des Raumes, Zeitschrift für Physik 10, 377-386 (1922). Première écriture des équations de Friedmann, dans le cas d'une coubure spatiale positive.
(de) Alexandre Friedmann, Über die Möglichkeit einer Welt mit konstanter negativer Krümmung des Raumes, Zeitschrift für Physik 21 326–332 (1924). Écriture des équations de Friedmann dans le cas d'une courbure spatiale négative.
(fr) Georges Lemaître, Un Univers homogène de masse constante et de rayon croissant rendant compte de la vitesse radiale des nébuleuses extragalactiques, Annales de la société scientifique de Bruxelles A47, 49-59 (1927).
(en) Georges Lemaître, A homogeneous Universe of constant mass and increasing accounting for the radial velocity of extragalactic nebulae, Monthly Notices of the Astronomical Society 91, 483–490 (1931). Traduction anglaise de l'article précédent par Arthur Eddington, mais amputé d'une phrase essentielle (voir expansion de l'univers).
(en) Howard P. Robertson, On the Foundations of Relativistic Cosmology, Proceedings of the National Academy of Sciences of the United States of America, 15, 822-829 (1929). Écriture unifiée des équations de Friedmann pour toute valeur de la courbure spatiale.
(en) Howard P. Robertson, Relativistic Cosmology, Review of Modern Physics 5, 62-90 (1933).
(en) Arthur G. Walker, On Milne's theory of wolrd's structure, Proceedings of the London Mathematical Society 42, 90-126 (1936). Résultat identiques à ceux de H. P. Robertson retrouvés indépendamment.

Portail de la cosmologie

Ce document provient de « %C3%89quations de Friedmann ».

Catégories : Article validé du portail cosmologie | Cosmologie | Relativité générale

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Équation de Friedman de Wikipédia en français (auteurs)

Игры ⚽ Нужен реферат?

Regardez d'autres dictionnaires:

FRIEDMAN (M.) — FRIEDMAN MILTON (1912 ) Économiste américain, professeur à l’université de Chicago à partir de 1948, journaliste, mais aussi conseiller économique d’organismes officiels (Federal Reserve Board), du Parti républicain et des présidents Nixon et… … Encyclopédie Universelle
Equation of exchange — In economics, the equation of exchange is the relation::Mcdot V = Pcdot Qwhere, for a given period,:M, is the total amount of money in circulation on average in an economy.:V, is the velocity of money, that is the average frequency with which a… … Wikipedia
Milton Friedman — Pour les articles homonymes, voir Friedman. Milton Friedman Milton Friedman Naissance 31 … Wikipédia en Français
Milton Fridman — Milton Friedman Pour les articles homonymes, voir Friedman. Milton Friedman Milton Friedman Naissance … Wikipédia en Français
Quantity theory of money — In economics, the quantity theory of money is a theory emphasizing the positive relationship of overall prices or the nominal value of expenditures to the quantity of money. Origins and development of the quantity theory The quantity theory… … Wikipedia
Phillips curve — The Phillips curve is a historical inverse relation between the rate of unemployment and the rate of inflation in an economy. Stated simply, the lower the unemployment in an economy, the higher the rate of increase in wages paid to labor in that… … Wikipedia
Hubble's law — Physical cosmology Universe · Big Bang … Wikipedia
Contributors to general relativity — General relativity Introduction Mathematical formulation Resources Fundamental concepts … Wikipedia
Money supply — Finance Financial markets Bond market … Wikipedia
Martin David Kruskal — Born September 28, 1925(1925 09 28) New York City … Wikipedia

Dictionnaires et Encyclopédies sur 'Academic'

Équation de Friedman

Équations de Friedmann

Sommaire

Les deux équations de Friedmann

Quelques solutions particulières

Univers de poussière

Univers de radiation

Constante cosmologique

Équation d'état constante

Solutions avec plusieurs espèces

Poussière et radiation

Poussière et constante cosmologique

Autres écritures

Interprétation

Dérivation des équations de Friedmann

Voir aussi

Liens internes

Références

Références générales actuelles

Articles historiques

Regardez d'autres dictionnaires:

Share the article and excerpts

Dictionnaires et Encyclopédies sur 'Academic'

Wikipédia en Français

Équation de Friedman

Équations de Friedmann

Sommaire

Les deux équations de Friedmann

Quelques solutions particulières

Univers de poussière

Univers de radiation

Constante cosmologique

Équation d'état constante

Solutions avec plusieurs espèces

Poussière et radiation

Poussière et constante cosmologique

Autres écritures

Interprétation

Dérivation des équations de Friedmann

Voir aussi

Liens internes

Références

Références générales actuelles

Articles historiques

Regardez d'autres dictionnaires:

Share the article and excerpts

Direct link