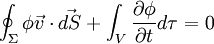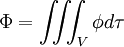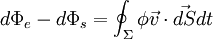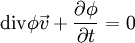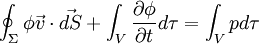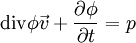Équations de conservation

Équations de conservation

Équation de conservation

Dans diverses disciplines de la physique, lorsqu'une quantité est supposée conservée (typiquement la masse, la charge ou le nombre baryonique) malgré son déplacement, on peut établir une équation reliant la variation de cette quantité dans le temps à sa variation dans l'espace, appelée équation de conservation de la grandeur.

Sommaire

Expression

On peut l'établir sous deux formes, intégrale et locale.

Forme intégrale

Soit une grandeur ϕ supposée conservée, se déplaçant selon un vecteur v. Alors pour tout volume V, de surface fermée Σ, on a :

\oint_{\Sigma} \phi \vec{v} \cdot \vec{dS} + \int_V \frac{\partial \phi}{\partial t} d\tau = 0

Autrement dit, le flux de ϕ à travers la surface implique une variation de ϕ dans le volume.

Preuve

Le volume V contient, à un instant t, la quantité :

\Phi = \iiint_V \phi d\tau

Cette quantité varie, pendant dt, à cause des apports ou des pertes extérieurs :

dΦ = dΦe − dΦs

Il est entré et sorti, en faisant un bilan algébrique :

d\Phi_e - d\Phi_s = \oint_{\Sigma} \phi \vec{v}\cdot \vec{dS} dt

Enfin, en différenciant Φ et en identifiant, on obtient bien la formule donnée.

Forme locale

Soit une grandeur ϕ supposée conservée, se déplaçant selon un vecteur v. Alors pour tout élément de volume d3τ, on a :

\mathrm{div} \phi \vec{v} + \frac{\partial \phi}{\partial t} = 0

Preuve

À partir de la forme intégrale, en utilisant le théorème de Green-Ostrogradski, pour un volume infinitésimal d3τ, on retrouve bien la formule donnée.

Terme source

Parfois, on peut établir une « équation de conservation » même s'il existe des sources qui font varier la grandeur. L'équation de conservation ne s'annule alors plus, et sa valeur dépend de la production des sources, appelé terme source. En notant p la production algébrique dans un volume infinitésimal :

\oint_{\Sigma} \phi \vec{v} \cdot \vec{dS} + \int_V \frac{\partial \phi}{\partial t} d\tau = \int_V p d\tau
\mathrm{div} \phi \vec{v} + \frac{\partial \phi}{\partial t} = p

Voir aussi

Articles connexes

  • Portail de la physique Portail de la physique
Ce document provient de « %C3%89quation de conservation ».

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Équations de conservation de Wikipédia en français (auteurs)

Игры ⚽ Поможем написать курсовую

Regardez d'autres dictionnaires:

  • Equations de Friedmann — Équations de Friedmann Le contenu de cet article du Portail:Cosmologie a fait l objet d une validation par un chercheur spécialiste du domaine le 18 juillet 2007 (comparer avec la version actuelle). Il est donc en principe exempt d erreur grave.… …   Wikipédia en Français

  • Équations de friedmann — Le contenu de cet article du Portail:Cosmologie a fait l objet d une validation par un chercheur spécialiste du domaine le 18 juillet 2007 (comparer avec la version actuelle). Il est donc en principe exempt d erreur grave. Ce label ne préjuge pas …   Wikipédia en Français

  • Équations de Navier-Stokes — Pour les articles homonymes, voir Stokes. En mécanique des fluides, les équations de Navier Stokes sont des équations aux dérivées partielles non linéaires qui décrivent le mouvement des fluides « newtoniens » (visqueux) dans… …   Wikipédia en Français

  • Équations de Friedmann — Alexander Friedmann. Les équations de Friedmann correspondent aux équations de la relativité générale (appelées équations d Einstein) écrites dans le contexte d un modèle cosmologique homogène et isotrope. Elles régissent donc l évolution du taux …   Wikipédia en Français

  • Equations de Maxwell — Équations de Maxwell  Ne doit pas être confondu avec Relations de Maxwell. Les équations de Maxwell, aussi appelées équations de Maxwell Lorentz, sont des lois fondamentales de la physique. Elles constituent les postulats de base de l… …   Wikipédia en Français

  • Équations de Maxwell pour les nuls — Équations de Maxwell  Ne doit pas être confondu avec Relations de Maxwell. Les équations de Maxwell, aussi appelées équations de Maxwell Lorentz, sont des lois fondamentales de la physique. Elles constituent les postulats de base de l… …   Wikipédia en Français

  • Équations de maxwell —  Ne doit pas être confondu avec Relations de Maxwell. Les équations de Maxwell, aussi appelées équations de Maxwell Lorentz, sont des lois fondamentales de la physique. Elles constituent les postulats de base de l électromagnétisme, avec l… …   Wikipédia en Français

  • Équations des ondes électromagnétiques — Équations de Maxwell  Ne doit pas être confondu avec Relations de Maxwell. Les équations de Maxwell, aussi appelées équations de Maxwell Lorentz, sont des lois fondamentales de la physique. Elles constituent les postulats de base de l… …   Wikipédia en Français

  • Equations fondamentales de la mecanique des milieux continus — Équations fondamentales de la mécanique des milieux continus Les équations fondamentales de la mécanique des milieux continus regroupent les énoncés mathématiques les plus couramment utilisés dans le cadre de la mécanique des milieux continus,… …   Wikipédia en Français

  • Équations fondamentales de la mécanique des milieux continus) — Équations fondamentales de la mécanique des milieux continus Les équations fondamentales de la mécanique des milieux continus regroupent les énoncés mathématiques les plus couramment utilisés dans le cadre de la mécanique des milieux continus,… …   Wikipédia en Français

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”