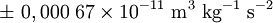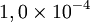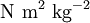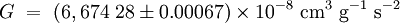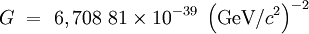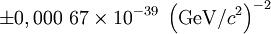Constante de Newton

Constante gravitationnelle

En physique, la constante de proportionnalité de la loi de la gravitation est notée 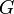$G\$ , et est appelée constante gravitationnelle, ou constante universelle de gravitation, ou constante de Newton, ou plus simplement grand G.

La constante gravitationnelle est une constante physique fondamentale qui apparaît dans la loi d'Isaac Newton sur la gravitation universelle et les lois qui en découlent (Lois de Képler,..).

La constante gravitationnelle apparaît aussi dans la théorie de la relativité générale d'Albert Einstein.

La force d'attraction entre deux corps massifs est proportionnelle au produit de leur masse et inversement proportionnelle au carré de la distance qui sépare leurs centres de masse respectifs.

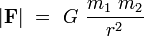
$|{\mathbf F}| \ = \ G \ \frac{m_1\ m_2}{r^2}$

Sommaire

1 Valeur
2 Comparaison avec les autres forces fondamentales
3 Mesures de la constante gravitationnelle
4 Constantes associées
- 4.1 Le paramètre gravitationnel standard
- 4.2 La constante gravitationnelle de Gauss
5 Les dimensions de
6 Voir aussi
7 Notes et références

Valeur

La constante gravitationnelle $G\,$ est une constante de proportionnalité de la force de gravitation c'est à dire d'attraction entre les corps; elle suit la loi en carré inverse des distances et est proportionnelle au produit des masses $m 1$ et $m 2$ .

Valeur dans le SI

$G\,$ correspond à la force entre deux masses d'un kilogramme chacune, distantes d'un mètre.

Dans les unités SI, le CODATA de 2006 recommande la valeur suivante :

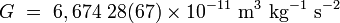$G\ =\ 6,674\ 28(67) \times 10^{-11} \ \mbox{m}^3 \ \mbox{kg}^{-1} \ \mbox{s}^{-2}$ ,

les chiffres entre parenthèses donnant la valeur de l'incertitude standard, qui est de :

$\plusmn\ 0,000\ 67 \times 10^{-11} \ \mbox{m}^3 \ \mbox{kg}^{-1} \ \mbox{s}^{-2}$

Soit une incertitude relative de :

$1,0 \times 10^{-4}$

En termes dimensionnels, on peut également exprimer cette constante en :

$\ \mbox{N} \ \mbox{m}^2 \ \mbox{kg}^{-2}$

Une autre estimation qui fait autorité est donnée par l'Union astronomique internationale (Standish 1995).

Valeur CGS

Dans le système CGS la valeur de la constante est :

$G\ =\ \left(6,674\ 28 \plusmn 0.00067 \right) \times 10^{-8} \ \mbox{cm}^3 \ \mbox{g}^{-1} \ \mbox{s}^{-2} \,$

Valeur GeV/c²

$G\ =\ 6,708\ 81 \times 10^{-39} \ \left(\mbox{GeV}/c^2\right)^{-2}$

Avec une incertitude standard de :

$\plusmn 0,000\ 67 \times 10^{-39} \ \left(\mbox{GeV}/c^2\right)^{-2}$

Valeur en unités naturelles

Dans les unités dites « naturelles », $G\,$ et les autres constantes physiques comme la vitesse de la lumière $c\,$ , ont une valeur de 1.

Comparaison avec les autres forces fondamentales

Quand on compare les quatre forces fondamentales : (force de gravitation, force électromagnétique, force faible, force forte), il apparait que la force de gravitation est extrêmement plus faible que les autres. Par exemple, la force de gravitation entre un électron et un proton séparés par un mètre serait d'environ 10^-67 newton, tandis que la force électromagnétique entre les deux mêmes particules à la même distance serait d'environ 10^-28 newton, c'est-à-dire 39 ordres de grandeur (ou 10³⁹ fois) plus importante.

Mesures de la constante gravitationnelle

La constante gravitationnelle est l'une des constantes les plus difficiles à mesurer.

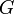${G} \$ a été mesurée directement la première fois par Henry Cavendish (Philosophical Transactions, 1798). Il utilisa une balance de torsion avec deux boules en mercure placées le long d'une tige horizontale. L'inertie des boules (reliée à la constante de torsion) permet de calculer la fréquence des oscillations de la balance. La très faible attraction causée par deux autres boules, placées indépendamment à l'extrémité de la tige, cause une légère modification des oscillations, et permet de calculer la force de gravité entre les boules, et ainsi la valeur de la constante de gravitation. Cavendish trouve 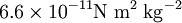$6.6 \times 10^{-11} {\rm N}\;{\rm m}^{2}\;{\rm kg}^{-2}$ . Cependant, son but n'était pas de mesurer cette constante, mais de mesurer la masse de la Terre.

La précision de la valeur mesurée de 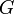${G} \$ a peu changé depuis cette première expérience. Cela est dû, non seulement à la faiblesse de la force de gravitation, mais aussi à l'impossibilité de s'affranchir réellement de la présence d'autres objets massifs (comme les murs du laboratoire...). Une très légère vibration du sol (provoquée par exemple par le passage d'un camion dans la rue) peut aussi compromettre la précision de la mesure. Une récente étude (Gillies, 1997) a montré que les valeurs publiées de la constante varient beaucoup, et que des mesures plus récentes et plus précises s'excluent mutuellement.

Constantes associées

Le paramètre gravitationnel standard

Article détaillé : paramètre gravitationnel standard.

Le produit 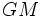${GM} \$ s'appelle le paramètre gravitationnel standard, noté 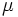${\mu} \$ (mu).

Ce paramètre fournit une simplification pratique des différentes formules liées à la gravitation.

Selon que 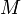${M} \$ désigne la masse de la Terre ou du Soleil, 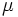${\mu} \$ s'appelle la constante gravitationnelle géocentrique ou héliocentrique.

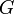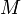En fait, pour la Terre et le Soleil, ce produit est connu avec une plus grande précision que celle associée à chacun des deux facteurs ${G} \$ et ${M} \$ . Il est ainsi possible d'utiliser la valeur du produit connue avec une plus grande précision, plutôt que de susbtituer les valeurs des deux paramètres.

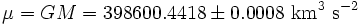Pour la Terre : $\mu = GM = 398 600.4418 \plusmn 0.0008 \ \mbox{km}^{3} \ \mbox{s}^{-2}$ .

La constante gravitationnelle de Gauss

De même, les calculs de la mécanique céleste peuvent être faits dans les unités de masse solaire plutôt que celles du Système international d'unités, comme le kilogramme.

Dans ce cas, on utilise la constante gravitationnelle de Gauss, qui se note 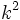${k^2} \$ , où :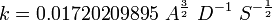

${k = 0.01720209895 \ A^{\frac{3}{2}} \ D^{-1} \ S^{-\frac{1}{2}} } \$

avec :

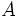${A} \$ est une unité astronomique,
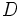${D} \$ est le jour solaire moyen,
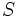${S} \$ est la masse solaire.

Si à la place du jour solaire moyen, on utilise l'année sidérale comme unité de temps, la valeur de 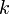${k} \$ est alors très proche de $2 \pi \$ .

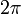Les dimensions de ${G} \$

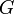
La valeur de 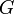${G} \$ dans les dimensions assignées à la constante gravitationnelle (le cube de la longueur en mètre, divisé par la masse en kg et le carré du temps en secondes) est celle couramment utilisée.

Cependant, cette valeur a une signification fondamentale selon les unités de Planck : la constante gravitationnelle est égale numériquement et aussi dimensionnellement au cube de la longueur de Planck, divisé par la masse de Planck et le carré du temps de Planck.

Finalement, ce sont ces unités de Planck qui sont les plus fondamentales, puisqu'elles représentent les plus petites quantités ayant un sens dans la physique moderne (et notamment la physique quantique).

En d'autres termes, on pourrait dire que 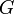${G} \$ est une constante fondamentale, puisqu'elle peut s'exprimer simplement en fonction des unités de Planck.

Voir aussi

Bibliographie

George T. Gillies. "The Newtonian gravitational constant: recent measurements and related studies". Reports on Progress in Physics, 60:151-225, 1997. (A lengthy, detailed review. See Figure 1 and Table 2 in particular. Available online: PDF)

E. Myles Standish. "Report of the IAU WGAS Sub-group on Numerical Standards". In Highlights of Astronomy, I. Appenzeller, ed. Dordrecht: Kluwer Academic Publishers, 1995. (Complete report available online: PostScript. Tables from the report also available: Astrodynamic Constants and Parameters)

Jens H. Gundlach and Stephen M. Merkowitz. "Measurement of Newton's Constant Using a Torsion Balance with Angular Acceleration Feedback". Physical Review Letters, 85(14):2869-2872, 2000. (Also available online: PDF)

Peter J. Mohr and Barry N. Taylor, CODATA recommended values of the fundamental physical constants: 2002 (Reviews of Modern Physics, 2005, vol.77, p. 1–107). PDF, Section Q (p. 42–47) décrit les expériences de mesures mutuellement exclusives à partir desquelles la valeur CODATA de G est dérivée.

Jean-Philippe Uzan & Roland Lehoucq, Les constantes fondamentales, Belin (2005) ISBN 2701136261. La section sur la constante de gravitation contient, entre autres, une traduction française des articles originaux de Maskeline, Cavendish sur la mesure de la constante de gravitation et une traduction des textes de Dirac, Gamow et Teller sur l'hypothèse d'une constante de gravitation variable.

Liens externes

Notes et références

Portail de la physique
Portail de l’astronomie

Ce document provient de « Constante gravitationnelle ».

Catégories : Constante fondamentale | Gravitation

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Constante de Newton de Wikipédia en français (auteurs)

Игры ⚽ Поможем написать реферат

Regardez d'autres dictionnaires:

Constante Gravitationnelle — En physique, la constante de proportionnalité de la loi de la gravitation est notée , et est appelée constante gravitationnelle, ou constante universelle de gravitation, ou constante de Newton, ou plus simplement grand G. La constante… … Wikipédia en Français
Constante de gravitation — Constante gravitationnelle En physique, la constante de proportionnalité de la loi de la gravitation est notée , et est appelée constante gravitationnelle, ou constante universelle de gravitation, ou constante de Newton, ou plus simplement grand… … Wikipédia en Français
Constante gravitationnelle — Ne doit pas être confondu avec g, accélération de la pesanteur à la surface de la Terre En physique, la constante de proportionnalité de la loi de la gravitation est notée , et est appelée constante gravitationnelle, ou constante… … Wikipédia en Français
Constante d’Einstein — Constante d Einstein En 1916, Albert Einstein propose de décrire l univers à l aide d une équation de champ, tensorielle. Celle ci contient deux constantes, qui n ont strictement rien à voir l une avec l autre. La première est la constante d… … Wikipédia en Français
newton — [ njutɔn ] n. m. • v. 1950; n. pr. ♦ Métrol. Unité de mesure de force (symb. N), correspondant à une accélération de 1 m/s2 communiquée à une masse de 1 kg. Newton mètre : unité de mesure de moment d une force (symb. Nm). ● newton nom masculin… … Encyclopédie Universelle
Constante des aires — Mouvement à force centrale En mécanique du point, un mouvement à force centrale est le mouvement d un point matériel soumis uniquement à une force centrale, c est à dire une force toujours dirigée vers le même point noté , appelé centre de force … Wikipédia en Français
Constante de gravitación universal — La constante de gravitación universal fue medida por primera vez por Henry Cavendish en 1798.La medida de G ha sido repetida por otros experimentadores con diversas mejoras y refinamientos. Todas las medidas de G son difíciles a causa de la… … Wikipedia Español
Constante d'Einstein — En 1916, Albert Einstein propose de décrire l univers à l aide d une équation de champ, tensorielle. Celle ci contient deux constantes, qui n ont strictement rien à voir l une avec l autre. La première est la constante d Einstein, figurée dans le … Wikipédia en Français
Constante de Pythagore — Racine carrée de deux L hypoténuse d un triangle rectangle isocèle de côté 1 vaut √2 La racine carrée de deux, notée √2, √2 ou 21/2, est définie comme le seul nombre réel positif qui, lorsqu il est multiplié p … Wikipédia en Français
Constante de Gauss — En mathématiques, la constante de Gauss, notée G, est l inverse de la moyenne arithmético géométrique de 1 et de la racine carrée de deux : Cette constante porte le nom du mathématicien allemand Carl Friedrich Gauss car il a découvert en… … Wikipédia en Français

Dictionnaires et Encyclopédies sur 'Academic'

Constante de Newton

Constante gravitationnelle

Sommaire