Sinus hyperbolique

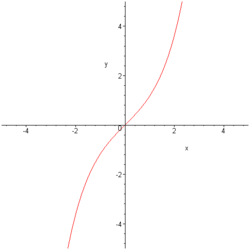
Graphe de la fonction sinus hyperbolique sur une partie de $\mathbb R$

Le sinus hyperbolique est, en mathématiques, une fonction hyperbolique.

Sommaire

1 Définition
2 Propriétés
3 Valeurs
4 Zéros
5 Fonction réciproque
6 Voir aussi

Définition

La fonction sinus hyperbolique, notée sinh ou sh est la fonction complexe suivante :

$\sinh : z \longmapsto \frac {e^z-e^{-z}}{2}$

où $e$ est le nombre exponentiel.

La fonction sinus hyperbolique est la partie impaire de la fonction exponentielle.

La fonction sinus hyperbolique est en quelque sorte l'analogue de la fonction sinus dans la géométrie hyperbolique.

Propriétés

Propriétés générales

sinh est continue et infiniment dérivable.
La dérivée de sinh est cosh, la fonction cosinus hyperbolique.
Les primitives de sinh sont cosh+C, à une constante d'intégration C près.
La restriction de sinh à $\mathbb R$ est impaire et strictement croissante.

Propriétés trigonométriques

De par les définitions des fonctions sinus et cosinus hyperbolique, on peut déduire les égalités suivantes :

$e^z = \cosh(z) + \sinh(z) \,$

$e^{-z} = \cosh(z) - \sinh(z) \,$

Ces égalités sont analogues à la formule d'Euler en trigonométrie classique.

De même que les coordonnées (cos(t), sin(t)) définissent un cercle, (cosh(t),sinh(t)) définissent la branche positive d'une hyperbole équilatérale. On a en effet pour t>0 :

$\cosh^2(t) - \sinh^2(t) = 1 \,$ .

D'autre part, pour $x \in \mathbb R$ :

$\sinh(i x) = \frac{e^{i x} - e^{-i x}}{2} = i \sin(x)$

$\sinh(x) = -i \sin(i x) \,$

$\sinh(x+y) = \sinh(x) \cosh(y) + \cosh(x) \sinh(y) \,$

$\sinh^2\left(\frac{x}{2}\right) = \frac{\cosh(x)-1}{2}$

L'utilisation de formules trigonométriques telles que tan(2t) = ^{(2 tan t)}⁄_{(1-tan² t)} permet aussi d'obtenir des relations plus anecdotiques, telle que (pour tout réel $x$ non nul) :

$\sinh(x) = \frac {-1} {\tan(2 \times \mathrm{Arctan}(e^x))}$ ;

voir également l'article Gudermannien

Développement en série de Taylor

sinh, étant indéfiniment dérivable, possède un développement en série de Taylor en tout point :

$\sinh z = z + \frac {z^3} {3!} + \frac {z^5} {5!} + \cdots = \sum_{n=0}^\infty \frac{z^{2n+1}}{(2n+1)!}$

Valeurs

Quelques valeurs de sinh :

$\sinh(0) = 0 \,$
$\sinh(1) = \frac {e^2-1}{2e}$
$\sinh(i) = i \sin(1) \,$

Zéros

Tous les zéros de $sinh$ sont des imaginaires purs : $z\in \mathbb{C}, \sinh(z)=0 \Leftrightarrow z \in \{i k \pi ; k \in \mathbb{Z}\}$ .

Démonstration

Soit $z = x + i$ $y$ avec $x,y \in \mathbb{R}$ alors $\sinh(x+i y)=\sinh(x)\cos(y)+i\sin(y)\cosh(x)=0 \Leftrightarrow \sin(y)=0 \mbox{ et } \sinh(x)=0 \Leftrightarrow y \in \{k \pi ; k \in \mathbb{Z}\} \mbox{ et } x=0$

Fonction réciproque

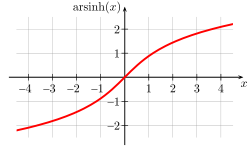
Graphe de la fonction argument sinus hyperbolique sur une partie de R

sinh admet une fonction réciproque, notée argsinh (ou argsh), et nommée argument sinus hyperbolique. Il s'agit d'une fonction multiforme complexe. Sa branche principale est généralement choisie en posant comme coupure les segments $\left]-\infty i;-i\right[$ et $\left]i;+\infty i\right[$ .

$\operatorname{argsinh}(z) = \ln\Big(z + \sqrt{1+z^2}\Big)$

Pour $x \in \mathbb R$ , la restriction de sinh à $\mathbb R$ admet une réciproque : $\operatorname{argsinh}(x)= \ln\Big(x + \sqrt{1+x^2}\Big)$ ; il est facile de démontrer ce résultat en utilisant que $\operatorname{ch}^2t-\operatorname{sh}^2t=1$ , et donc, en posant $\operatorname{sh}t=x$ on aura $e^t=\operatorname{sh} t+\operatorname{ch} t= x+\sqrt {1+x^2}$ .

Voir aussi

Sur les autres projets Wikimedia :

« la fonction sinus hyperbolique », sur Wikimedia Commons (ressources multimédia)

Sur les autres projets Wikimedia :

« la fonction argsinus hyperbolique », sur Wikimedia Commons (ressources multimédia)

Portail de l'analyse

Catégories :

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Sinus hyperbolique de Wikipédia en français (auteurs)

Игры ⚽ Поможем написать реферат

Regardez d'autres dictionnaires:

Sinus hyperbolique d'un réel x — ● Sinus hyperbolique d un réel x réel noté sh x égal à … Encyclopédie Universelle
Fonction sinus hyperbolique — ● Fonction sinus hyperbolique fonction définie sur R : x ↦ sh x. (Sa dérivée est la fonction cosinus hyperbolique.) … Encyclopédie Universelle
hyperbolique — [ ipɛrbɔlik ] adj. • 1541; lat. hyperbolicus, gr. huperbolikos I ♦ Rhét. Caractérisé par l hyperbole. Style hyperbolique. Cour. Des compliments hyperboliques. ⇒ emphatique, grandiloquent. Philos. Le doute hyperbolique (Descartes). II ♦ (1646) 1 ♦ … Encyclopédie Universelle
Hyperbolique — Fonction hyperbolique En mathématiques, on appelle fonctions hyperboliques les fonctions cosinus hyperbolique, sinus hyperbolique et tangente hyperbolique. Les noms de sinus, cosinus et tangente proviennent de leur ressemblance avec les fonctions … Wikipédia en Français
sinus — 1. sinus [ sinys ] n. m. • 1539; mot lat. « courbe » → sein ♦ Anat. 1 ♦ Cavité irrégulière (de certains os). Sinus de la face, de certains os de la face (sinus frontal, maxillaire, sinus sphénoïdaux). Spécialt, cour. Inflammation des sinus (de la … Encyclopédie Universelle
Sinus — Cette page d’homonymie répertorie les différents sujets et articles partageant un même nom. Sur les autres projets Wikimedia : « sinus », sur le Wiktionnaire (dictionnaire universel) Sinus est un mot latin signifiant… … Wikipédia en Français
Sinus (mathématique) — Fonction trigonométrique Pour les articles homonymes, voir Cosinus (homonymie), Tangente et Sinus. Toutes les valeurs des fonctions trigonométriques en u … Wikipédia en Français
Sinus (mathématiques) — Fonction trigonométrique Pour les articles homonymes, voir Cosinus (homonymie), Tangente et Sinus. Toutes les valeurs des fonctions trigonométriques en u … Wikipédia en Français
Fonction Hyperbolique — En mathématiques, on appelle fonctions hyperboliques les fonctions cosinus hyperbolique, sinus hyperbolique et tangente hyperbolique. Les noms de sinus, cosinus et tangente proviennent de leur ressemblance avec les fonctions trigonométriques (ou… … Wikipédia en Français
Fonction hyperbolique — En mathématiques, on appelle fonctions hyperboliques les fonctions cosinus hyperbolique, sinus hyperbolique et tangente hyperbolique. Les noms de sinus, cosinus et tangente proviennent de leur ressemblance avec les fonctions trigonométriques (ou… … Wikipédia en Français

Dictionnaires et Encyclopédies sur 'Academic'

Sinus hyperbolique

Sommaire

Définition