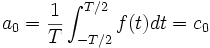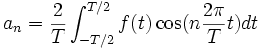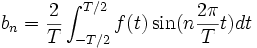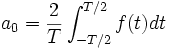Théorème de Bessel-Parseval-Plancherel

L'égalité de Parseval (parfois appelée également Théorème de Parseval ou Identité de Rayleigh) est une formule fondamentale de la théorie des séries de Fourier. On la doit au mathématicien français Marc-Antoine Parseval. Cette formule peut être interprétée comme une généralisation du théorème de Pythagore pour les séries dans les espaces de Hilbert.

Dans de nombreuses applications physiques (courant électrique par exemple), cette formule peut s'interpréter comme suit : l'énergie totale s'obtient en sommant les contributions des différents harmoniques.

L'énergie totale d'un signal ne dépend pas de la représentation choisie : fréquentielle ou temporelle.

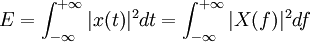
Sommaire 1 Inégalité de Bessel 2 Formule pour les séries de Fourier 2.1 Applications 2.2 Réciproque : théorème de Riesz-Fischer

Inégalité de Bessel

Si (e_i) avec i élément d'un ensemble I est une famille orthonormée, alors pour tout h dans H un espace préhilbertien, on note c_i(h) = <h|e_i> (par convention, le produit scalaire est linéaire à gauche, antilinéaire à droite). L'inégalité de Bessel affirme la convergence absolue de la série suivante et la majoration :

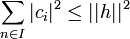
Elle indique aussi que l'ensemble des termes non nuls est au plus dénombrable. Si h est dans l'adhérence de l'espace vectoriel engendré par la famille (e_i), alors la majoration est une égalité, nommée égalité de Parseval. Ainsi, si la famille est une base de Hilbert, l'égalité est toujours vérifiée.

Elle existe aussi dans le cas où le préhilbertien est de dimension finie, elle s'applique par exemple en analyse harmonique sur un groupe abélien fini.

Formule pour les séries de Fourier

On suppose que f est T-périodique et de carré intégrable (c'est donc valable notamment pour f continue par morceaux). On définit les coefficients de Fourier de f :

.

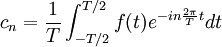L'égalité de Parseval affirme la convergence de la série suivante et énonce l'identité :

.

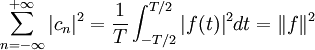Si la fonction f est à valeurs réelles, on peut adopter les conventions suivantes :

L'égalité de Parseval devient :

.

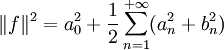Attention : certains auteurs préfèrent une convention pour laquelle l'expression de a₀ est aussi en 2/T : (si f est paire)

La formule de Parseval devient alors :

.

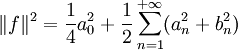Applications

• Si deux fonctions de carré intégrable f et g ont le même spectre en fréquences (mêmes coefficients de Fourier), alors les coefficients de Fourier de f-g sont tous nuls (par linarité) et 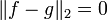. De fait, f et g sont égales presque partout. Si de plus f et g sont continues par morceaux, f et g sont égales hormis au niveau des points de discontinuité de f et de g.
• Lorsque l'intégrale est plus facile à calculer que la série, l'égalité de Parseval est un moyen de calculer un certain nombre de séries numériques (on peut aussi utiliser l'égalité en un point entre la fonction et sa série de Fourier, donnée par exemple par le théorème de Dirichlet).
• L'égalité de Parseval permet d'obtenir l'inégalité de Wirtinger entre les normes d'une fonction périodique et de sa dérivée, puis l'inégalité isopérimétrique classique.

Réciproque : théorème de Riesz-Fischer

On note l'espace vectoriel des suites c_n (n entier relatif), telle que la série de terme général | c_n | ² converge.

Le théorème de Riesz-Fischer permet d'énoncer qu'une telle suite c_n est la suite des coefficients de Fourier d'une fonction de carré intégrable, T périodique.

Ainsi il y a isomorphisme entre les espaces 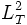des fonctions de carré intégrable et T périodiques et 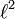. La formule de Parseval montre qu'il s'agit même d'une isométrie.

• Portail des mathématiques