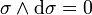Theoreme de Frobenius

Theoreme de Frobenius

Théorème de Frobenius

En géométrie différentielle, le théorème de Frobenius est un théorème décrivant la structure de certaines formes différentielles possédant certaines propriétés.

Formulation

Dans sa version moderne, le théorème de Frobenius peut s'exprimer ainsi :

Soient r formes linéaires 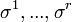{\mathbf \sigma}^1, ..., {\mathbf \sigma}^r linéairement indépendantes en un point p d'une variété différentielle, et soient des formes 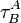{\mathbf \tau}^A_B, A et B décrivant l'ensemble 1, ..., r, telles que
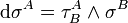{\rm d} {\mathbf \sigma}^A = {\mathbf \tau}^A_B \wedge {\mathbf \sigma}^B,
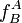d désignant la dérivée extérieure et \wedge le produit extérieur, alors il existe un voisinage ouvert de p dans lequel il existe des fonctions f^A_B, hB telles que pour tout A :
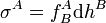{\mathbf \sigma}^A = f^A_B {\rm d} h^B.

Conséquence fondamentale

Dans le cas d'une seule forme σ, le théorème de Frobenius stipule que

{\mathbf \sigma} \wedge {\rm d} {\mathbf \sigma} = 0

est équivalent à dire que σ est de la forme

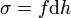{\mathbf \sigma} = f {\rm d} h,

c'est-à-dire que σ est proportionnelle à un gradient.

En termes de composantes, cette relation s'écrit :

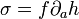σ[a,bσc] = 0 équivalent à \sigma = f \partial_a h.

Cette dernière relation est abondamment utilisée en relativité générale, où elle permet d'exhiber que certains champs de vecteurs sont parallèles à un gradient, et peuvent définir un feuilletage de la région considérée, correspondant aux hypersurfaces où la fonction dont on prend le gradient (ici notée h) prend une valeur constante.

Généralisation

Une généralisation du théorème de Frobenius peut se faire à l'aide du théorème de Darboux.

  • Portail des mathématiques Portail des mathématiques
Ce document provient de « Th%C3%A9or%C3%A8me de Frobenius ».

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Theoreme de Frobenius de Wikipédia en français (auteurs)

Игры ⚽ Поможем сделать НИР

Regardez d'autres dictionnaires:

  • Théorème de Frobénius — Théorème de Frobenius En géométrie différentielle, le théorème de Frobenius est un théorème décrivant la structure de certaines formes différentielles possédant certaines propriétés. Formulation Dans sa version moderne, le théorème de Frobenius… …   Wikipédia en Français

  • Théorème de frobenius — En géométrie différentielle, le théorème de Frobenius est un théorème décrivant la structure de certaines formes différentielles possédant certaines propriétés. Formulation Dans sa version moderne, le théorème de Frobenius peut s exprimer… …   Wikipédia en Français

  • Théorème de Frobenius — En géométrie différentielle, le théorème de Frobenius est un théorème décrivant la structure de certaines formes différentielles possédant certaines propriétés. Formulation Dans sa version moderne, le théorème de Frobenius peut s exprimer… …   Wikipédia en Français

  • Theoreme de Frobenius generalise — Théorème de Frobenius généralisé Le théorème de Frobenius généralisé est un théorème d algèbre générale qui étend le théorème de Frobenius de 1877. En 1843, Hamilton a souhaité étendre les propriétés d algèbre normée des nombres complexes en… …   Wikipédia en Français

  • Théorème de frobenius généralisé — Le théorème de Frobenius généralisé est un théorème d algèbre générale qui étend le théorème de Frobenius de 1877. En 1843, Hamilton a souhaité étendre les propriétés d algèbre normée des nombres complexes en considérant des triplets de réels. Il …   Wikipédia en Français

  • Théorème de Frobenius généralisé — Pour les articles homonymes, voir Théorème de Hurwitz. Le théorème de Frobenius généralisé (connu également sous le nom de théorème de Hurwitz[1], bien que ce dernier en soit une forme plus générale encore) est un théorème d algèbre générale qui… …   Wikipédia en Français

  • Theoreme des facteurs invariants — Théorème des facteurs invariants En mathématiques, le théorème des facteurs invariants porte sur les modules de type fini sur les anneaux principaux. Les facteurs invariants sont des obstructions à l inversibilité des matrices qui n apparaissent… …   Wikipédia en Français

  • Théorème des facteurs invariants — En mathématiques, le théorème des facteurs invariants porte sur les modules de type fini sur les anneaux principaux. Les facteurs invariants sont des obstructions à l inversibilité des matrices qui n apparaissent pas dans la théorie des espaces… …   Wikipédia en Français

  • Theoreme de Perron-Frobenius — Théorème de Perron Frobenius Pour les articles homonymes, voir Perron. Ce théorème porte le nom des mathématiciens Oskar Perron et Ferdinand Georg Frobenius. Si une matrice réelle A a tous ses coefficient strictements positifs, alors son rayon… …   Wikipédia en Français

  • Théorème de perron-frobenius — Pour les articles homonymes, voir Perron. Ce théorème porte le nom des mathématiciens Oskar Perron et Ferdinand Georg Frobenius. Si une matrice réelle A a tous ses coefficient strictements positifs, alors son rayon spectral est une valeur propre… …   Wikipédia en Français

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”