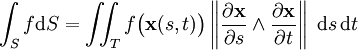Integrale de surface
- Integrale de surface
-
Intégrale de surface
En mathématiques, une intégrale de surface est une intégrale définie sur toute une surface qui peut être courbe dans l'espace. Pour une surface donnée, on peut intégrer sur un champ scalaire ou sur un champ vectoriel.
Les intégrales de surface ont de nombreuses applications dans la théorie classique de l'électromagnétisme.
Intégrale de surface sur un champ scalaire
Pour trouver une formule explicite de l'intégrale de surface, il faut généralement paramétrer la surface S en question en considérant un système de coordonnées curvilignes, comme la longitude et la latitude sur une sphère. Une fois le paramétrage x(s,t) trouvé, où s et t varie dans une région du plan, l'intégrale de surface d'un champ scalaire est donnée par :
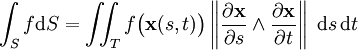
De plus l'aire de S est donnée par :
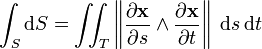 .
.
Voir aussi
 Portail des mathématiques
Portail des mathématiques
Catégories : Analyse vectorielle | Aire
Wikimedia Foundation.
2010.
Contenu soumis à la licence CC-BY-SA. Source : Article Integrale de surface de Wikipédia en français (auteurs)
Regardez d'autres dictionnaires:
Intégrale De Surface — En mathématiques, une intégrale de surface est une intégrale définie sur toute une surface qui peut être courbe dans l espace. Pour une surface donnée, on peut intégrer sur un champ scalaire ou sur un champ vectoriel. Les intégrales de surface… … Wikipédia en Français
Intégrale de surface — En mathématiques, une intégrale de surface est une intégrale définie sur toute une surface qui peut être courbe dans l espace. Pour une surface donnée, on peut intégrer sur un champ scalaire ou sur un champ vectoriel. Les intégrales de surface… … Wikipédia en Français
intégrale de surface — paviršinis integralas statusas T sritis fizika atitikmenys: angl. area integral; surface integral vok. Flächenintegral, n rus. поверхностный интеграл, m pranc. intégrale de surface, f … Fizikos terminų žodynas
Intégrale de surface ou intégrale d'une fonction sur une surface — ● Intégrale de surface ou intégrale d une fonction sur une surface flux de cette fonction à travers la surface … Encyclopédie Universelle
intégrale — ● intégrale nom féminin Œuvre complète d un écrivain, d un musicien : L intégrale des cantates de Bach. Limite, lorsqu elle existe, de sommes d un nombre indéfiniment croissant d éléments indéfiniment petits construits en divisant indéfiniment le … Encyclopédie Universelle
Integrale curviligne — Intégrale curviligne En mathématiques, l intégrale curviligne est une intégrale où la fonction à intégrer est évaluée sur une courbe. Sommaire 1 Analyse complexe 1.1 Exemple … Wikipédia en Français
Intégrale Curviligne — En mathématiques, l intégrale curviligne est une intégrale où la fonction à intégrer est évaluée sur une courbe. Sommaire 1 Analyse complexe 1.1 Exemple … Wikipédia en Français
Surface (homoymie) — Cette page d’homonymie répertorie les différents sujets et articles partageant un même nom. la surface est un espace géométrique, Voir aussi catégorie:surface (en géométrie) Lexique des surfaces Microsoft Surface : une table tactile. grande… … Wikipédia en Français
Surface de Gauss — En électromagnétisme, une surface de Gauss est une surface imaginaire de l espace utilisée dans le calcul des champs électriques par le théorème de Gauss. Puisque le théorème de Gauss peut être utilisé dans le cas de certaines symétries… … Wikipédia en Français
Intégrale curviligne — En mathématiques, l intégrale curviligne est une intégrale où la fonction à intégrer est évaluée sur une courbe. Sommaire 1 Analyse complexe 1.1 Exemple … Wikipédia en Français
 .
.