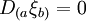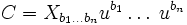- Tenseur de killing
-
Tenseur de Killing
GénéralitésMathématiquesTenseur (mathématiques)
Produit tensoriel
... de deux modules
... de deux applications linéaires
Algèbre tensorielle
Champ tensoriel
Espace tensorielPhysiqueConvention d'Einstein
Tenseur métrique
Tenseur énergie-impulsion
Tenseur de Riemann
... de Ricci
... d'Einstein
... de Weyl
... de Levi-Civita
... de Killing
... de Killing-Yano
... de Bel-Robinson
... de Cotton-York
Tenseur électromagnétique
Tenseur des contraintes
Tenseur des déformationsArticles connexesPortail des MathématiquesPortail de la PhysiqueEn géométrie différentielle, un tenseur de Killing est un tenseur qui satisfait à une équation analogue à celle d'un vecteur de Killing, l'équation de Killing.
Sommaire
Définition
Un tenseur symétrique ξ est un tenseur de Killing s'il vérifie :
où D est la dérivée covariante associée à la métrique riemannienne de la variété considérée, et les parenthèses désignent le fait que l'on a symétrisé l'équation sur les indices a et b.
Cette équation peut formellement se généraliser à un tenseur X d'ordre n quelconque sous la forme :
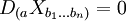 .
.
Tout tenseur obéissant à une telle équation est un tenseur de Killing. [1]
Interprétation géométrique
Il n'existe pas d'interprétation géométrique simple d'un tenseur de Killing. Par contre ceux-ci possèdent la même propriété que les vecteurs de Killing vis-à-vis des géodésiques, à savoir qu'ils permettent de définir une constante du mouvement si on les contracte avec le vecteur tangent u à une géodésique.
La quantité C définie par :
est en effet constante le long d'une géodésique.
Ceci permet dans certain cas la résolution explicite des équations du mouvement dans un espace possédant un tenseur de Killing. C'est en particulier le cas dans la métrique de Kerr où un tel tenseur a été trouvé par Brandon Carter dans les années 1960. On parle de la constante de Carter, qui assure qu'un mouvement dans la géométrie de Kerr est intégrable [2].
Il prend ainsi un rôle important dans la compréhension des trajectoires décrites en relativité générale.
Tenseurs de Killing-Yano
Il existe une autre généralisation du concept de vecteur de Killing à des tenseurs d'ordre plus élevé. Il s'agit des tenseurs de Killing-Yano, introduits en 1952 par Yano[3].
Voir aussi
Articles connexes
Références
- ↑ (fr) Notes de lecture sur les métriques en relativité générale.
- ↑ (fr) Conférence : « Sources d'ondes gravitationnelles pour LISA » [pdf], Luc Blanchet, CNRS/Institut d'Astrophysique de Paris.
- ↑ (en) Kentarô Yano, Annals of Mathematics, 55, 328 (1952).
Bibliographie
- « Sur les transformations de variété riemanniennes et kähleriennes », Annales de l'Institut Fourier, tome 9 (1959), p 147-248.
- Portail de la géométrie
- Portail de la physique
Catégorie : Géométrie riemannienne
Wikimedia Foundation. 2010.