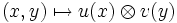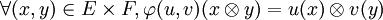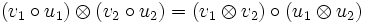- Produit tensoriel de deux applications lineaires
-
Produit tensoriel de deux applications linéaires
GénéralitésMathématiquesTenseur (mathématiques)
Produit tensoriel
... de deux modules
... de deux applications linéaires
Algèbre tensorielle
Champ tensoriel
Espace tensorielPhysiqueConvention d'Einstein
Tenseur métrique
Tenseur énergie-impulsion
Tenseur de Riemann
... de Ricci
... d'Einstein
... de Weyl
... de Levi-Civita
... de Killing
... de Killing-Yano
... de Bel-Robinson
... de Cotton-York
Tenseur électromagnétique
Tenseur des contraintes
Tenseur des déformationsArticles connexesPortail des MathématiquesPortail de la PhysiqueLe produit tensoriel de deux applications linéaires est une construction qui à deux applications linéaires u d'un A-module E1 dans F1, et v d'un A-module E2 dans F2, associe une troisième application linéaire
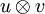 du produit tensoriel
du produit tensoriel 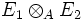 dans le produit tensoriel
dans le produit tensoriel 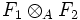 .
.Définition
On suppose dans cette partie que l'anneau d'opérateurs A des modules étudiés est commutatif. Avec les notations introduites en introduction, l'application suivante de
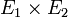 dans
dans 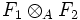
est une application A-bilinéaire. D'après la propriété universelle du produit tensoriel, il existe une application
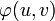 de
de 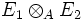 dans
dans 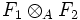 telle que :
telle que :En fait, l'application
 de l'espace
de l'espace  dans le module
dans le module 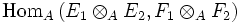 est bilinéaire, il existe donc une application
est bilinéaire, il existe donc une application 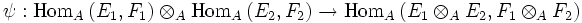 telle que :
telle que :-
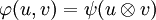 pour toutes applications A-linéaires
pour toutes applications A-linéaires 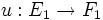 ,
, 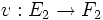 .
.
L'application φ(u,v) de
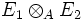 dans
dans 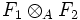 s'appelle le produit tensoriel de u et v, et il se note dans la pratique
s'appelle le produit tensoriel de u et v, et il se note dans la pratique 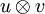 . Attention, cette notation est abusive, car elle peut désigner deux objets de nature différente :
. Attention, cette notation est abusive, car elle peut désigner deux objets de nature différente :- L'application A-linéaire
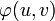
- L'élément du produit tensoriel
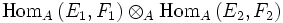 qui n'est pas une application linéaire.
qui n'est pas une application linéaire.
D'autant plus que ψ ne réalise pas systèmatiquement un isomorphisme de
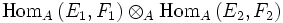 sur
sur 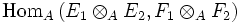 , si bien qu'il est impossible d'identifier les deux «
, si bien qu'il est impossible d'identifier les deux « 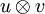 ».
».Néanmoins, quand tous les modules E1,E2,F1,F2 ont des bases finies (ce qui en particulier le cas lorsque l'on manipule des espaces vectoriels de dimension finie), alors ψ est un isomorphisme, et cela a bien un sens de confondre les deux notations
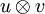 .Démonstration de ce résultat
.Démonstration de ce résultatNotons
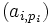 une base de Ei pour i = 1 ou 2, et
une base de Ei pour i = 1 ou 2, et 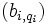 une base de Fi pour i = 1 ou 2. Pour tout couple (p1,p2) on pose
une base de Fi pour i = 1 ou 2. Pour tout couple (p1,p2) on pose 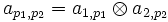 , la famille ainsi définie
, la famille ainsi définie 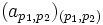 est une base du produit tensoriel
est une base du produit tensoriel 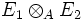 .
.De manière analogue, on définit une base
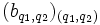 du produit tensoriel
du produit tensoriel 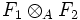 .
.Notons
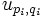 l'application A-linéaire
l'application A-linéaire 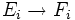 telle que
telle que 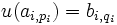 et
et 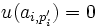 pour
pour 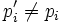 .
.Comme toutes les familles manipulées sont finies, la famille
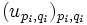 est une base du module
est une base du module 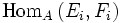 (attention, ce résultat a priori serait faux si la famille était infinie).
(attention, ce résultat a priori serait faux si la famille était infinie).On définit
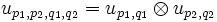 l'élément de
l'élément de 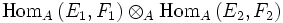 . La famille
. La famille 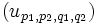 est une base finie de ce module.
est une base finie de ce module.Or l'image par ψ de
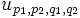 est l'application A-linéaire
est l'application A-linéaire 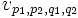 définie de cette manière :
définie de cette manière :-
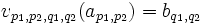
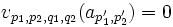 pour tout
pour tout 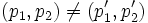 .
.
Il est clair que cette famille constitue une base du module
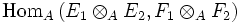 . ψ envoie une base sur une base, c'est donc un A-isomorphisme.
. ψ envoie une base sur une base, c'est donc un A-isomorphisme.Propriétés
- Si E1,E2,F1,F2,G1,G2 sont six modules, et si on se donne des applications linéaires
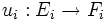 ,
, 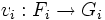 , alors
, alors
- Si ui est un isomorphisme de Ei sur Fi et vi est l'isomorphisme réciproque, alors
-
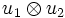 est inversible et son inverse est
est inversible et son inverse est 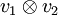 .
.
Catégorie : Algèbre -
Wikimedia Foundation. 2010.