Tenseur de weyl

En géométrie riemannienne, le tenseur de Weyl, nommé en l'honneur d'Hermann Weyl, représente la partie du tenseur de Riemann ne possédant pas de trace.

Sommaire 1 Formule principale 2 Interprétation physique 3 Propriétés 3.1 Composantes indépendantes 3.2 Transformation conforme 4 Classification 5 Voir aussi

Formule principale

En notant R_abcd, R_ab, R et g_ab le tenseur de Riemann, le tenseur de Ricci, la courbure scalaire et le tenseur métrique, le tenseur de Weyl C_abcd s'écrit

,

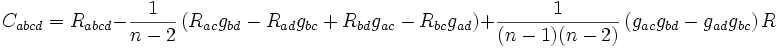où n est la dimension de l'espace considéré. En particulier, en relativité générale, où l'on considère presque exclusivement des espaces-temps de dimension 4, on a

,

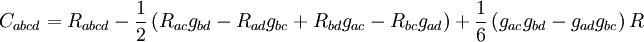Interprétation physique

En relativité générale, le tenseur de Ricci est lié à la présence de matière ; en l'absence de matière, le tenseur de Ricci est nul. Par conséquent, le tenseur de Weyl s'identifie au tenseur de Riemann. Cette propriété donne toute son importance au tenseur de Weyl : sa structure donne la totalité de la structure du champ gravitationnel dans les régions vides de matière. Par exemple, une région de l'espace traversée par une onde gravitationnelle a un tenseur de Weyl non nul.

Propriétés

Composantes indépendantes

Le nombre de composantes indépendantes du tenseur de Riemann est (n + 1)n²(n − 1) / 12, celui du tenseur de Ricci est n(n + 1) / 2 (en incluant sa trace, correspondant à la courbure scalaire, et pour n supérieur à 2). Le nombre de composantes du tenseur de Weyl est donc, pour n supérieur à 2, de

.

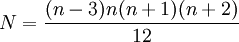N est nul à une ou deux dimensions. En particulier, le tenseur de Weyl est nul dans un espace à 3 dimensions. Dans un espace(-temps) à 4 dimensions, il possède 10 composantes indépendantes.

Transformation conforme

Un calcul direct montre que si l'on fait subir au tenseur métrique une transformation conforme (c'est-à-dire qu'à partir d'une fonction Ω on définit un nouveau tenseur sous la forme 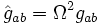), le tenseur de Weyl associé reste invariant. Comme le tenseur de Weyl est nul dans l'espace de Minkowski, le tenseur de Weyl doit être nul dans un espace conformément plat (c'est-à-dire dont la métrique est proportionnelle à celle de Minkowski en tout point). On peut montrer que la réciproque est vrai pour n supérieur à 3 : il suffit que le tenseur de Weyl soit nul pour que l'espace soit conformément plat. Dans un espace à trois dimensions, où le tenseur de Weyl est nul par définition, la platitude conforme est équivalente à l'annulation d'un autre tenseur, appelé tenseur de Cotton-York (ou tenseur de Cotton).

Classification

Un grand nombre de solutions connues des équations de la relativité générale correspondent à des espaces dépourvus de matière. Il est donc particulièrement utile de classer ces différentes solutions. L'une de ces classifications exploite une analogie avec les vecteurs propres des espaces vectoriels usuels, appliqué aux tenseurs d'ordre 4. Cette classification s'appelle la classification de Petrov. Dans un contexte légèrement différent, les espaces-temps quadridimensionnels sont commodément étudiés dans le cadre du formalisme de Newman-Penrose, qui consiste essentiellement à choisir un système de coordonnées adapté et dont les vecteurs de base jouissent de certaines propriétés. Dans ce cadre-là, les dix composantes indépendantes du tenseur de Weyl sont réduite à la donnée de cinq nombres complexes appelés scalaires de Weyl, auxquels il est possible de donner une interprétation physique intuitive (alors que la nature exacte de la solution apparaît souvent peu claire par la simple considération du tenseur métrique).

Voir aussi

• Classification de Petrov
• Formalisme de Newman-Penrose
• Scalaire de Weyl
• Tenseur de Cotton-York

• Portail de la géométrie
• Portail de la physique