Tenseur de levi-civita

Tenseur de levi-civita: Tenseur de Levi-Civita

Articles scientifiques
sur les tenseurs

Généralités

Tenseur

Mathématiques

Tenseur (mathématiques)
Produit tensoriel
... de deux modules
... de deux applications linéaires
Algèbre tensorielle
Champ tensoriel
Espace tensoriel

Physique

Convention d'Einstein
Tenseur métrique
Tenseur énergie-impulsion
Tenseur de Riemann
... de Ricci
... d'Einstein
... de Weyl
... de Levi-Civita
... de Killing
... de Killing-Yano
... de Bel-Robinson
... de Cotton-York
Tenseur électromagnétique
Tenseur des contraintes
Tenseur des déformations

Articles connexes

Modules
Algèbre extérieure

Portail des Mathématiques

Portail de la Physique

Le tenseur de Levi-Civita – ou tenseur dualiseur – est un tenseur défini à partir du symbole de Levi-Civita d'ordre N .

Étant donné un espace de dimension $N$ , le symbole de Levi-Civita d'ordre N 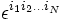$\epsilon^{i_1 i_2 \ldots i_N}$ , aussi appelé pseudo-tenseur unité complètement antisymétrique n'est pas un tenseur. Par exemple, ses composantes devraient être multipliées par $2 N$ lorsque le système de coordonnées est réduit d'un facteur 2.

Sommaire

1 Définition du tenseur dualiseur

1.1 Tenseur dualiseur en coordonnées contravariantes

1.2 Tenseur dualiseur en coordonnées covariantes

1.3 Détermination du signe

2 Propriétés du tenseur dualiseur

2.1 Produit de tenseurs dualiseurs

2.1.1 Résultat d'ordre 2

2.1.2 Résultat d'ordre 4

2.2 Nullité de la dérivée covariante du tenseur dualiseur

3 Définition de tenseurs duaux au sens de Hodge

3.1 Tenseurs duaux en dimension 3

3.2 Tenseur duaux en dimension 4

4 Voir aussi

Définition du tenseur dualiseur

Tenseur dualiseur en coordonnées contravariantes

La formule
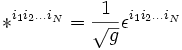
$*^{i_1 i_2 \ldots i_N} = \frac{1}{\sqrt{g}}\epsilon^{i_1 i_2 \ldots i_N}$
où $g$ est le déterminant du tenseur métrique, définit bien un tenseur à partir du symbole de Levi-Civita d'ordre N. Ce tenseur, aussi appelé tenseur de Levi-Civita et noté 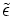$\tilde{\epsilon}$ est appelé tenseur dualiseur. Pour un scalaire (soit un tenseur d'ordre 0), il faut qu'il soit indépendant du choix du système de coordonnées. Le déterminant du tenseur métrique n'est donc pas un tenseur mais son produit avec le symbole $ε$ est bien un tenseur, indépendant du système de coordonnées.

Tenseur dualiseur en coordonnées covariantes

On passe aux coordonnées covariantes en mettant en jeu $N$ fois le tenseur métrique. Le produit de ces $N$ termes avec le Symbole de Levi-Civita d'ordre N est égal au déterminant du tenseur métrique et l'on obtient :
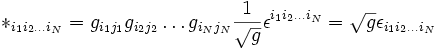
$*_{i_1 i_2 \ldots i_N} = g_{i_1 j_1} g_{i_2 j_2} \ldots g_{i_N j_N} \frac{1}{\sqrt{g}}\epsilon^{i_1 i_2 \ldots i_N} = \sqrt{g} \epsilon_{i_1 i_2 \ldots i_N}$
Détermination du signe

Le tenseur dualiseur garde néanmoins un caractère particulier. C'est le choix de la détermination de la racine carrée qui définit l'orientation du système de coordonnées. Retourner une coordonnée doit s'accompagner du changement de signe des composantes du tenseur.

Dans le cas de l'espace-temps quadridimensionnel, le déterminant du tenseur métrique est négatif. Deux possibilités s'offrent alors, considérer que le tenseur dualiseur est imaginaire pur, ou remplacer $g$ par $- g$ . Cette seconde possibilité facilite les calculs mais n'est pas satisfaisante d'un point de vue théorique (connecter avec la mesure de la distance spatiale ou temporelle comme racine carrée de l'intervalle d'espace-temps, dont le signe donne la nature, temps ou espace).

Propriétés du tenseur dualiseur

Produit de tenseurs dualiseurs

Les formules suivantes découlent directement des formules obtenues avec le symbole de Levi-Civita d'ordre N. Le symbole 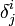$\delta^i_j$ est le symbole de Kronecker, représentant le tenseur unité.

Résultat d'ordre 2
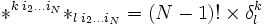
$*^{k \; i_2\ldots i_N}*_{l \; i_2 \ldots i_N} = \left(N-1\right) ! \times \delta^k_l$
Résultat d'ordre 4
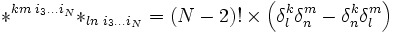
$*^{k m \; i_3\ldots i_N}*_{l n \; i_3 \ldots i_N} = \left(N-2\right) ! \times \left(\delta^k_l \delta^m_n - \delta^k_n \delta^m_l\right)$
Nullité de la dérivée covariante du tenseur dualiseur

La dérivée covariante du tenseur dualiseur est nulle :
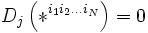$D_j \left(*^{i_1 i_2 \ldots i_N}\right) = 0$ .

Démonstration

L'expression de la dérivée covariante à partir de la dérivée simple et des symboles de Christoffel donne
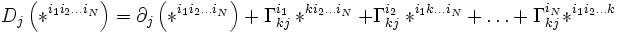
$D_j \left(*^{i_1 i_2 \ldots i_N}\right) = \partial_j \left(*^{i_1 i_2 \ldots i_N}\right) + \Gamma^{i_1}_{k j} *^{k i_2 \ldots i_N} + \Gamma^{i_2}_{k j} *^{i_1 k \ldots i_N} + \ldots + \Gamma^{i_N}_{k j} *^{i_1 i_2 \ldots k}$
Réécrivons premier terme sous la forme
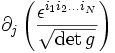$\partial_j \left(\frac{\epsilon^{i_1 i_2 \ldots i_N}}{\sqrt{\det{g}}}\right)$ .
Le symbole de Levi-Civita d'ordre N étant constant, ce terme devient
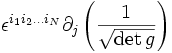$\epsilon^{i_1 i_2 \ldots i_N}\partial_j \left(\frac{1}{\sqrt{\det{g}}}\right)$ .
Dans la liste des termes suivants, le premier se réduit à sa valeur pour laquelle $k = i 1$ , le deuxième à sa valeur pour laquelle $k = i 2$ , etc. La somme des N termes vaut donc 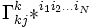$\Gamma^{k}_{k j} *^{i_1 i_2 \ldots i_N}$ . Étant donné l'expression de la contraction du symbole de Christoffel
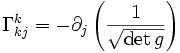$\Gamma^k_{k j} = - \partial_j \left(\frac{1}{\sqrt{\det g}}\right)$ ,
on trouve
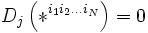$D_j \left(*^{i_1 i_2 \ldots i_N}\right) = 0$ .
∎

Définition de tenseurs duaux au sens de Hodge

Le produit du tenseur dualiseur avec un tenseur d'ordre $M$ dans un espace de dimension $N$ définit un tenseur d'ordre $N - M$ , son dual au sens de Hodge.
$\left[* a\right]^{i_1 i_2 \ldots i_{N-M}} = \frac{1}{M !} *^{i_1 i_2 \ldots i_N} a_{i_{N-M+1} \ldots i_N}$
Le produit met ici arbitrairement en jeu les $M$ derniers indices du tenseur dualiseur. On aurait aussi bien pu prendre les $M$ premiers indices. Les deux conventions diffèrents d'un signe - dans certains cas.

Tenseurs duaux en dimension 3

Un vecteur $b k$ possède un tenseur antisymétrique dual
$\left[* b\right]_{ij} = *_{ijk} b^k$ .
Réciproquement, le dual d'un tenseur antisymétrique $a i j$ est un vecteur
$\left[*a\right]^i = \frac{1}{2} \times *^{ijk} a_{jk}.$
Le dual du dual est le vecteur ou le tenseur antisymétrique lui-même. En effet, on a pour un vecteur
$\left[**b\right]^i = \frac{1}{2} *^{ijk} \left[*b\right]_{jk} = \frac{1}{2} *^{ijk} *_{jkl} b^l = \delta^i_l b^l = b^i$
et pour un tenseur antisymétrique
$\left[**a\right]^{ij} = \frac{1}{2} *^{ijk} \left[*a\right]_{k} = \frac{1}{2} *^{ijk} *_{klm} a^{lm} = \frac{1}{2}\left(\delta^{ij}_{lm} - \delta^{ij}_{ml}\right) a^{lm} = a^{ij}$
Tenseur duaux en dimension 4

Cette section est vide, pas assez détaillée ou incomplète. Votre aide est la bienvenue !

Voir aussi

Dualité de Hodge

Ce document provient de « Tenseur de Levi-Civita ».

Catégories : Calcul tensoriel | Système de coordonnées curvilignes

Contenu soumis à la licence CC-BY-SA. Source : Article Tenseur de levi-civita de Wikipédia en français (auteurs)

Игры ⚽ Нужно решить контрольную?

Regardez d'autres dictionnaires:

Tenseur de Levi-Civita — Le tenseur de Levi Civita – ou tenseur dualiseur – est un tenseur défini à partir du symbole de Levi Civita d ordre N . Étant donné un espace de dimension N, le symbole de Levi Civita d ordre N , aussi appelé pseudo tenseur unité complètement… … Wikipédia en Français
Symbole de levi-civita d'ordre n — Sommaire 1 Définition 2 Exemple 3 Tenseur dualiseur 4 Formules // … Wikipédia en Français
Symbole de Levi-Civita d'ordre N — Sommaire 1 Définition 2 Exemple 3 Tenseur dualiseur 4 Formules Définition Le symbole de Levi Civita d ordre N, généralement noté … Wikipédia en Français
Symbole de levi-civita — Le symbole de Levi Civita, noté ε (lettre grecque epsilon), est un indicateur antisymétrique d ordre 3 qui peut être exprimé à partir du symbole de Kronecker : Visualisation d un symbole de Levi Civita en 3 dimensions … Wikipédia en Français
Symbole de Levi-Civita — Le symbole de Levi Civita, noté ε (lettre grecque epsilon), est un indicateur antisymétrique d ordre 3 qui peut être exprimé à partir du symbole de Kronecker : Visualisation d un symbole de Levi Civita en 3 dimensions.(i d avant en arrière,… … Wikipédia en Français
Tenseur dualiseur — Tenseur de Levi Civita Articles scientifiques sur les tenseurs Généralités Tenseur Mathématiques Tenseur (mathématiques) Produit tensoriel ... de deux modules ... de deux applications linéaires Algèbre tensorielle Champ tensoriel Espace tensoriel … Wikipédia en Français
Tenseur de Cotton — York Articles scientifiques sur les tenseurs Généralités Tenseur Mathématiques Tenseur (mathématiques) Produit tensoriel ... de deux modules ... de deux applications linéaires Algèbre tensorielle Champ tensoriel Espace tensoriel … Wikipédia en Français
Tenseur de Maxwell — Tenseur électromagnétique Articles scientifiques sur les tenseurs Généralités Tenseur Mathématiques Tenseur (mathématiques) Produit tensoriel ... de deux modules ... de deux applications linéaires Algèbre tensorielle Champ tensoriel Espace… … Wikipédia en Français
Tenseur de champ électromagnétique — Tenseur électromagnétique Articles scientifiques sur les tenseurs Généralités Tenseur Mathématiques Tenseur (mathématiques) Produit tensoriel ... de deux modules ... de deux applications linéaires Algèbre tensorielle Champ tensoriel Espace… … Wikipédia en Français
Tenseur de cotton-york — Articles scientifiques sur les tenseurs Généralités Tenseur Mathématiques Tenseur (mathématiques) Produit tensoriel ... de deux modules ... de deux applications linéaires Algèbre tensorielle Champ tensoriel Espace tensoriel … Wikipédia en Français

Dictionnaires et Encyclopédies sur 'Academic'

Tenseur de levi-civita

Tenseur de Levi-Civita

Sommaire

Définition du tenseur dualiseur

Tenseur dualiseur en coordonnées contravariantes

Tenseur dualiseur en coordonnées covariantes

Détermination du signe

Propriétés du tenseur dualiseur

Produit de tenseurs dualiseurs

Résultat d'ordre 2

Résultat d'ordre 4

Nullité de la dérivée covariante du tenseur dualiseur

Définition de tenseurs duaux au sens de Hodge

Tenseurs duaux en dimension 3

Tenseur duaux en dimension 4

Voir aussi

Regardez d'autres dictionnaires:

Share the article and excerpts

Dictionnaires et Encyclopédies sur 'Academic'

Wikipédia en Français

Tenseur de levi-civita

Tenseur de Levi-Civita

Sommaire

Définition du tenseur dualiseur

Tenseur dualiseur en coordonnées contravariantes

Tenseur dualiseur en coordonnées covariantes

Détermination du signe

Propriétés du tenseur dualiseur

Produit de tenseurs dualiseurs

Résultat d'ordre 2

Résultat d'ordre 4

Nullité de la dérivée covariante du tenseur dualiseur

Définition de tenseurs duaux au sens de Hodge

Tenseurs duaux en dimension 3

Tenseur duaux en dimension 4

Voir aussi

Regardez d'autres dictionnaires:

Share the article and excerpts

Direct link