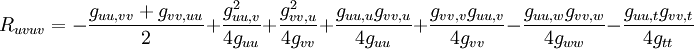- Tenseur de courbure
-
Tenseur de Riemann
GénéralitésMathématiquesTenseur (mathématiques)
Produit tensoriel
... de deux modules
... de deux applications linéaires
Algèbre tensorielle
Champ tensoriel
Espace tensorielPhysiqueConvention d'Einstein
Tenseur métrique
Tenseur énergie-impulsion
Tenseur de Riemann
... de Ricci
... d'Einstein
... de Weyl
... de Levi-Civita
... de Killing
... de Killing-Yano
... de Bel-Robinson
... de Cotton-York
Tenseur électromagnétique
Tenseur des contraintes
Tenseur des déformationsArticles connexesPortail des MathématiquesPortail de la PhysiqueEn géométrie différentielle, le tenseur de courbure de Riemann est la façon la plus courante d'exprimer la courbure des variétés riemanniennes, ou plus générale d'une variété disposant d'une connexion affine, avec ou sans torsion.
Soit deux géodésiques d'un espace courbe, parallèles au voisinage d'un point P. Dans un espace courbe, des géodésiques parallèles en un point ne vont pas forcément le rester en d'autres points de l'espace. Le tenseur de courbure de Riemann exprime l'évolution de ces géodésiques l'une par rapport à l'autre. Plus l'espace est courbe, plus les géodésiques vont se rapprocher ou s'éloigner rapidement.
Sommaire
Définition
Le tenseur de courbure est formulé à l'aide d'une connexion de Levi-Civita (ou plus généralement d'une connexion affine)
 (ou dérivée covariante) par la formule suivante :
(ou dérivée covariante) par la formule suivante :Pour tout vecteur u, v et w de la variété :
![R(u,v)w =\nabla_u\nabla_v w - \nabla_v \nabla_u w -\nabla_{[u,v]} w .](/pictures/frwiki/52/461317856ee33357e6bacdd676c3efd5.png)
où
![[\ ,\ ]](/pictures/frwiki/99/c5f866165522f9acfdb8efa9bd62ac17.png) est le crochet de Lie.
est le crochet de Lie.Ici R(u,v) est une transformation linéaire selon chacun de ses arguments sur l'espace tangent de la variété.
NB : certains auteurs définissent le tenseur de courbure comme du signe opposé.
Si
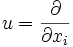 et
et 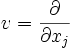 sont des champs de vecteur de coordonnées, alors [u,v] = 0 et on peut ré-écrire la formule :
sont des champs de vecteur de coordonnées, alors [u,v] = 0 et on peut ré-écrire la formule :Le tenseur de courbure mesure alors la non-commutativité de la dérivée covariante.
La transformation linéaire
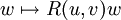 est aussi appelée la transformation de courbure ou endomorphisme.
est aussi appelée la transformation de courbure ou endomorphisme.En termes de coordonnées, cette équation peut être ré-écrite en utilisant les symboles de Christoffel :

Symétries et identités
Le tenseur de courbure de Riemann a les symétries suivantes :
La dernière identité a été découverte par Ricci, mais est souvent nommé première identité de Bianchi ou identité algébrique de Bianchi.
Ces trois identités forment une liste complète des symétries de tenseur de courbure, c'est-à-dire qu'étant donné un tenseur respectant les identités ci-dessus, on peut trouver une variété de Riemann disposant d'un tel tenseur de courbure en un point. De simples calculs mathématiques montrent qu'un tel tenseur a n2(n2 − 1) / 12 composants indépendants.
Il est possible de déduire une autre identité utile à partir de ces trois équations :
L'identité de Bianchi (souvent appelée seconde identité de Bianchi ou identité différentielle de Bianchi) implique les dérivées covariantes :
Étant donné un référentiel donné en un point d'une variété, les identités précédentes peuvent être écrites en termes des composants du tenseur de Riemann comme :
![6R_{a[bcd]}^{}=0](/pictures/frwiki/50/2a2a3fd99efd482625edb6c75296c353.png) (première identité de Bianchi)
(première identité de Bianchi)
![6R_{ab[cd;e]}^{}=0](/pictures/frwiki/100/d98f8764e7d6255ae16da8dda424ff0f.png) (seconde identité de Bianchi)
(seconde identité de Bianchi)
où les crochets correspondent au crochet de Lie, qualifiant les symétrisations selon les indices, et le point-virgule représente la dérivée covariante.
Tenseur de Riemann d'une surface
Gauss a trouvé une formule de la courbure K d'une surface par un calcul assez compliqué mais plus simple en coordonnées de Riemann où elle est égale au tenseur de Riemann dit « entièrement covariant » Rxyxy qui s'écrit alors, en deux dimensions[1],[2]. [3]
où gxx et gyy sont les coefficients de la métrique en coordonnées de Riemann, c'est-à-dire des coordonnées cartésiennes locales. Pour prendre un exemple, on ne peut utiliser le même système de coordonnées en Australie qu'en France sinon les Australiens auraient la tête en bas (pour nous)!
En coordonnées de Gauss, la formule étant compliquée, nous nous limiterons à une métrique diagonale[4] :
où, pour simplifier l'écriture, la virgule indique une dérivation partielle. guu et gvv sont les coefficients de la métrique en coordonnées de Gauss u et v (le "mollusque" d'Einstein). Les u et v peuvent être remplacés par n'importe quel système de coordonnées, la formule restera valable, par exemple en coordonnées sphériques où u et v sont remplacés par θ et φ. Il peut être pratique d'utiliser la forme en déterminant de la formule précédente, dite de Brioschi :
Pour une métrique non diagonale, la courbure de Gauss est[5] :
où E = guu, G = gvv et F = guv. Les indices correspondent à des dérivations partielles, sans la virgule utilisée précédemment.
Tenseur de Riemann d'un espace à quatre dimensions
Une surface est plongée dans notre espace à trois dimensions. Lorsqu'on ajoute deux dimensions, on obtient une hypersurface à quatre dimensions (u,v,w,t) plongée dans un espace à cinq dimensions. Pour obtenir le tenseur de Riemann de cet espace, on rajoute deux termes supplémentaires dans l'expression du tenseur de Riemann d'une surface qui devient[6]
Le tenseur de Riemann d'une métrique diagonale a six composantes non nulles Ruvuv, Ruwuw, Rvwvw,pour l'espace à trois dimensions plus Rutut, Rvtvt, Rwtwt, pour l'extension à quatre dimensions.
Notes et références
- ↑ Bernard Schaeffer, Relativités et quanta clarifiés, Publibook, 2007
- ↑ En toute rigueur on devrait utiliser ici u et v au lieu de x et y car il s'agit de coordonnées de Gauss
- ↑ Pauli, W, Theory of Relativity, Dover, 1981
- ↑ Riemannian geometry
- ↑ Gaussian curvature sur Wikipedia
- ↑ Brown, Kevin, « Reflections on Relativity »
Voir aussi
- Portail de la physique
Catégories : Article à recycler (physique) | Géométrie différentielle | Relativité générale | Tenseur
Wikimedia Foundation. 2010.

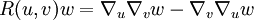
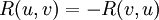

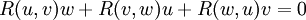
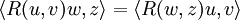
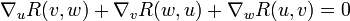
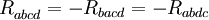
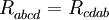


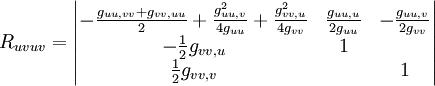
![K = \frac{1} {(EG-F^2)^2}\left[
\begin{vmatrix} -\frac{1}{2}E_{vv} + F_{uv} - \frac{1}{2}G_{uu} & \frac{1}{2}E_u & F_u-\frac{1}{2}E_v\\F_v-\frac{1}{2}G_u & E & F\\\frac{1}{2}G_v & F & G \end{vmatrix}-\begin{vmatrix} 0 & \frac{1}{2}E_v & \frac{1}{2}G_u\\\frac{1}{2}E_v & E & F\\\frac{1}{2}G_u & F & G \end{vmatrix}\right]](/pictures/frwiki/50/2cb397604db9faab9261412b16394047.png)