Espace Tensoriel
- Espace Tensoriel
-
Wikimedia Foundation.
2010.
Contenu soumis à la licence CC-BY-SA. Source : Article Espace Tensoriel de Wikipédia en français (auteurs)
Regardez d'autres dictionnaires:
Espace tensoriel — Soit E un module sur un anneau commutatif unitaire A. On appelle tenseur p fois contravariant et q fois covariant sur E tout élément du produit tensoriel , où E * est le module dual de E. Soit u un automorphisme du A module E, tu est le morphisme … Wikipédia en Français
espace tensoriel — tenzorinė erdvė statusas T sritis fizika atitikmenys: angl. tensor space vok. Tensorraum, m rus. тензорное пространство, n pranc. espace tensoriel, m … Fizikos terminų žodynas
Espace Euclidien — En mathématiques, un espace euclidien est un objet algébrique permettant de généraliser de façon naturelle la géométrie traditionnelle développée par Euclide, dans ses Éléments. Une géométrie de cette nature modélise, en physique classique, le… … Wikipédia en Français
Espace euclidien (algèbre linéaire) — Espace euclidien En mathématiques, un espace euclidien est un objet algébrique permettant de généraliser de façon naturelle la géométrie traditionnelle développée par Euclide, dans ses Éléments. Une géométrie de cette nature modélise, en physique … Wikipédia en Français
Espace euclidien — En mathématiques, un espace euclidien est un objet algébrique permettant de généraliser de façon naturelle la géométrie traditionnelle développée par Euclide, dans ses Éléments. Une géométrie de cette nature modélise, en physique classique, le… … Wikipédia en Français
ESPACE-TEMPS — La mécanique classique, sous la forme mathématique rigoureuse que lui a donnée Newton, repose sur les deux concepts fondamentaux d’espace et de temps absolus: un événement ponctuel est parfaitement déterminé lorsqu’on connaît sa position dans… … Encyclopédie Universelle
Espace Compact En Relativité — En relativité restreinte, un espace compact ou espace fermé est un espace fini et sans bord. Pour avoir une idée qualitative de cette notion, penser au jeu vidéo Pac Man : chaque plan dans lequel se déplace Pac Man est « fermé », c … Wikipédia en Français
Espace compact en relativite — Espace compact en relativité En relativité restreinte, un espace compact ou espace fermé est un espace fini et sans bord. Pour avoir une idée qualitative de cette notion, penser au jeu vidéo Pac Man : chaque plan dans lequel se déplace Pac… … Wikipédia en Français
Espace De Fock — L’espace de Fock est un espace de Hilbert utilisé en physique quantique pour décrire les états quantiques avec un nombre variable ou inconnu de particules. L’espace de Fock se définit comme l’espace de Hilbert obtenu par la somme directe des… … Wikipédia en Français
Espace de fock — L’espace de Fock est un espace de Hilbert utilisé en physique quantique pour décrire les états quantiques avec un nombre variable ou inconnu de particules. L’espace de Fock se définit comme l’espace de Hilbert obtenu par la somme directe des… … Wikipédia en Français
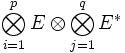 , où E * est le module dual de E.
, où E * est le module dual de E.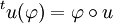 . On peut définir une action du groupe linéaire GL(E) sur
. On peut définir une action du groupe linéaire GL(E) sur 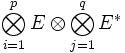 par :
par :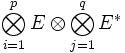 stable par la loi externe
stable par la loi externe 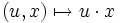 .
.