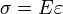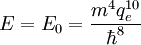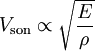Module de young

Module de young

Module de Young

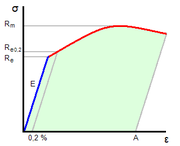
Le module de Young ou module d'élasticité (longitudinale) ou encore module de traction est la constante qui relie la contrainte de traction (ou de compression) et la déformation pour un matériau élastique isotrope.

Le physicien britannique Thomas Young (1773-1829) avait remarqué que le rapport entre la contrainte de traction appliquée à un matériau et la déformation qui en résulte (un allongement relatif) est constant, tant que cette déformation reste petite et que la limite d'élasticité du matériau n'est pas atteinte. La loi d'élasticité est la loi de Hooke :

Diagramme contrainte-déformation
\sigma = E \varepsilon

où :

  • σ est la contrainte (en unité de pression),
  • E est le module de Young (en unité de pression),
  • \varepsilon est l'allongement relatif (adimensionnel).

Le module de Young est la contrainte mécanique qui engendrerait un allongement de 100 % de la longueur initiale d'un matériau (il doublerait donc de longueur), si l'on pouvait l'appliquer réellement : dans les faits, le matériau se déforme de façon permanente, ou se rompt, bien avant que cette valeur soit atteinte.

Un matériau dont le module de Young est très élevé est dit rigide. L'acier, l'iridium, le diamant, sont des matériaux très rigides, l'aluminium et le plomb le sont moins, les matières plastiques et organiques sont généralement peu rigides. Il ne faut cependant pas confondre élasticité et rigidité puisque la raideur d'une poutre par exemple dépend de son module de Young mais aussi du moment d'inertie de sa section.

Note
Il ne faut pas confondre rigidité et raideur. La rigidité caractérise les matériaux, la raideur concerne les produits et les constructions. Une pièce mécanique massive en matière plastique peut être beaucoup plus raide qu'un ressort en acier.

Sommaire

Unités

D'après l'équation aux dimensions, le module de Young est homogène à une pression, ou plus précisément une contrainte. L'unité internationale est donc le pascal (Pa). Cependant, en raison des valeurs élevées que prend ce module, il est en général donné en mégapascal (MPa) ou newton par millimètre carré (N/mm2).

Expression théorique

Dans le cas d'un matériau cristallin et certains matériaux amorphes, le module de Young exprime la « force de rappel » électrostatique qui tend à maintenir les atomes à distance constante. Il peut s'exprimer en fonction de la dérivée seconde du potentiel interatomique.

Dans le système d'unités « naturelles » atomique, le module de Young, pour un matériau isotrope, est homogène à[1] :

E = E_0 = \frac{m^4 q_e^{10}}{\hbar^8}

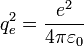où q_e^2 = \frac{e^2}{4 \pi \varepsilon_0}.

Ceci dit, compte tenu des problèmes où il apparaît (bilaplacien), il paraît assez naturel de le rationaliser soit

  • comme E1 = E0 / (16π2), soit
  • comme E2 = E0 / 64π6,

les ordres de grandeur de E1 ou E2 sont à comparer aux valeurs tabulées, de l'ordre de 100 GPa, qui apparaissent alors relever de ce corpus théorique.

Dans le cas des polymères, c'est l'agitation thermique qui « tortille » la chaîne carbonée qui tend à maintenir la longueur de la chaîne constante. Le module de Young peut alors s'exprimer en fonction de l'entropie.

Cette différence de comportement est flagrante lorsque l'on considère l'influence de la température ; si l'on soumet une éprouvette à une charge constante :

  • lorsque l'on augmente la température, une éprouvette de métal s'allonge (dilatation), donc son module de Young diminue, tandis que l'éprouvette en polymère se raccourcit (les chaînes s'agitent, s'entortillent) donc son module de Young augmente ;
  • lorsque l'on diminue la température, on observe le phénomène inverse : l'éprouvette de métal se raccourcit (contraction) donc son module de Young augmente, tandis que l'éprouvette de polymère s'allonge (les chaînes sont moins agitées et se laissent étirer) donc son module de Young diminue.

Relations

Avec le module de cisaillement (G) et le coefficient de Poisson (ν) :

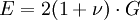E = 2(1+\nu)\cdot G.

Avec λ et μ appelées coefficients de Lamé :

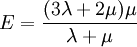E = \frac{(3{\lambda}+2{\mu}){\mu}}{{\lambda}+{\mu}}.

Les méthodes de mesure du module d'Young

Le plus simple reste bien sûr de réaliser un essai de traction. Et, connaissant les dimensions de l'éprouvette, d'en déduire le module de Young E. Cependant, il est difficile de réaliser cette mesure avec une bonne précision.

C'est pourquoi on préfère, lorsque cela est possible, déduire le module de Young de la fréquence propre de vibration d'une tige de matériau maintenue à ses extrémités et chargée en son milieu.

Article connexe : Méthode d'Oberst.

On peut aussi mesurer la vitesse du son dans le matériau qui nous intéresse, et en déduire le module de Young sachant qu'on a la relation suivante :

V_{\rm son} \propto \sqrt{\frac{E}{\rho}}

Cependant, cette loi est approchée : la vitesse du son dépend aussi du coefficient de Poisson.

Le module de Young augmente avec la vitesse de déformation.

Le module de Young complexe peut être déterminé par DM(T)A.

Quelques valeurs numériques de modules d'Young

Les caractéristiques mécaniques des matériaux sont variables d'un échantillon à l'autre. D'un point de vue global, selon M. Ashby, on trouve des matériaux dont la valeur est comprise entre 10kPa (mousses) et 1000GPa (céramiques technique). Il faut toujours distinguer le module d'Young d'un matériau à l'"état naturel" (valeurs ci-après), d'un matériau ayant subi un traitement (thermique ou de surface) dont la valeur de E peut doubler. Néanmoins, pour les calculs, on peut considérer en bonne approximation les valeurs suivantes.

Métaux purs
Matériaux Module (MPa)
Aluminium (Al)  69 000
Argent (Ag)  83 000
Baryum (Ba)  13 000
Béryllium (Be)  240 000
Bismuth (Bi)  32 000
Cadmium (Cd)  50 000
Césium (Cs)  1 700
Chrome (Cr)  289 000
Cobalt (Co)  209 000
Cuivre (Cu)  124 000
Étain (Sn)  41 500
Fer (Fe)  196 000
Germanium (Ge)  89 600
Indium (In)  11 000
Iridium (Ir)  528 000
Lithium (Li)  4 900
Magnésium (Mg)  45 000
Manganèse (Mn)  198 000
Molybdène (Mo)  329 000
Nickel (Ni)  214 000
Niobium (Nb)  105 000
Or (Au)  78 000
Palladium (Pd)  121 000
Platine (Pt)  168 000
Plomb (Pb)  18 000
Plutonium (Pu)  96 000
Rhodium (Rh)  275 000
Rubidium (Rb)  2 400
Ruthénium (Ru)  447 000
Scandium (Sc)  74 000
Sélénium (Se)  10 000
Sodium (Na)  10 000
Tantale (Ta)  186 000
Titane (Ti)  114 000
Tungstène (W)  406 000
Uranium (U)  208 000
Vanadium (V)  128 000
Zinc (Zn)  78 000
Zirconium (Zr)  68 000
Alliages
Matériaux Module (MPa)
Acier de construction  210 000
Acier à ressorts  220 000
Acier inoxydable 18-10  203 000
Bronze (cuivre + 9 à 12% d'étain)  124 000
Bronze au Béryllium  130 000
Cuivre laminé U4 (Recuit)  90 000
Cuivre laminé U4 (Écroui dur)  150 000
Duralumin AU4G  75 000
Fontes  83 à 170 000
Hastelloy B2 (Ni + Mo)  217 000
Hastelloy C 2000 (Ni + Cr + Mo)  206 000
Inconel X-750 (Ni + Cr + Fe)  212 à 218 000
Invar  140 000
Monel 400 (Ni + Cu)  173 000
Nimonic 90 (Ni + Cr + Co)  213 à 240 000
Nispan (Ni + Cr + Ti)  165 à 200 000
Phynox (Co + Cr + Ni + Mo)  203 400
Verres, céramiques, oxydes, carbures métalliques, minéraux
Matériaux Module (MPa)
Arsenic (As)  8 000
Arséniure de gallium (AsGa)  85 500
Béton 20 000
Brique  14 000
Calcaire (carbonate de calcium CaCO3, pierres)  20 à 70 000
Carbure de chrome (Cr3C2)  373 130
Carbure de silicium (SiC)  450 000
Carbure de Titane (TiC)  440 000
Carbure de tungstène (WC)  650 000
Carbure de zirconium (ZrC)  380 à  440 000
Diamant (C)  1 000 000
Graphite  30 000
Granite  60 000
Marbre  26 000
Mullite (Al6Si2O13)  145 000
Alumine (Oxyde d'Aluminium Al2O3)  390 000
Oxyde de béryllium (BeO)  30 000
Oxyde de magnésium (MgO)  250 000
Oxyde de zirconium (ZrO)  200 000
Saphir  420 000
Silice (oxyde de silicium SiO2)  107 000
Titanate d'aluminium (Ti3Al)  140 000
Titanate de baryum (BaTiO3)  67 000
Verre  69 000
Bois
Matériaux Module (MPa)
Acajou (Afrique)  12 000
Bambou  20 000
Bois de rose (Brésil)  16 000
Bois de rose (Inde)  12 000
Chêne  12 000
Contreplaqué glaw  12 400
Épicéa  13 000
Érable  10 000
Frêne  10 000
Papier  3 000 à 4 000
Séquoia  9 500

N.B. Ces valeurs sont celles du module d'élasticité dans le sens parallèle au fil (bois = matériau anisotrope). Dans une même essence, celui-ci varie en fonction de l'humidité, de la densité (qui n'est évidemment pas constante, bois = matériau hétérogène) et d'autres caractéristiques (longueur des fibres...).
Polymères, fibres
Matériaux Module (MPa)
caoutchoucs  700 à 4 000[2]
Fibre de carbone haut module  640 000
Fibre de carbone haute résistance  240 000
Kevlar  34 500
Nanotubes (Carbone)  1 100 000
Nylon  2 000 à 5 000
Plexiglas (Polyméthacrylate de méthyle)  2 380
Polyamide  3 000 à 5 000
Polycarbonate  2 300
Polyéthylène  200 à 700
Polystyrène  3 000 à 3 400
Résines époxy  3 500
Biomatériaux
Matériaux Module (MPa)
Cartilage  24
Cheveux  10 000
Collagène  6
Fémur  17 200
Humérus  17 200
Piquant d'oursin  15 000 à 65 000
Radius  18 600
Soie d'araignée  60 000
Tibia  18 100
Vertèbre cervicale  230
Vertèbre lombaire  160

Utilisations

Médecine 

La mesure des variations du module de Young dans un organe est une possibilité de l'imagerie médicale qui permet de représenter l'élasticité des tissus même profonds, par exemple pour donner l'étendue de la fibrose d'un foie ou détecter dans un sein un carcinome petit ou profond, peu décelable à la palpation (élastographie de 2e génération).

Références

  1. ↑ Charles Kittel (trad. Nathalie Bardou, Évelyne Kolb), Physique de l’état solide [« Solid state physics »], 1998 [détail des éditions] , chapitre 3.
  2. ↑ Pourquoi le caouthouc s'étire?
  • Ch. KITTEL , physique du solide, éd. Dunod ; chapitre : constantes d'élasticité.
  • Portail de la physique Portail de la physique
Ce document provient de « Module de Young ».

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Module de young de Wikipédia en français (auteurs)

Игры ⚽ Поможем написать реферат

Regardez d'autres dictionnaires:

  • Module De Young — Le module de Young ou module d élasticité (longitudinale) ou encore module de traction est la constante qui relie la contrainte de traction (ou de compression) et la déformation pour un matériau élastique isotrope. Le physicien britannique Thomas …   Wikipédia en Français

  • Module d'Young — Module de Young Le module de Young ou module d élasticité (longitudinale) ou encore module de traction est la constante qui relie la contrainte de traction (ou de compression) et la déformation pour un matériau élastique isotrope. Le physicien… …   Wikipédia en Français

  • Module de Young — Le module de Young ou module d élasticité (longitudinale) ou encore module de traction est la constante qui relie la contrainte de traction (ou de compression) et la déformation pour un matériau élastique isotrope. Le physicien britannique Thomas …   Wikipédia en Français

  • module d’Young — tampros modulis statusas T sritis Standartizacija ir metrologija apibrėžtis Statmenojo įtempio ir santykinės ilginės deformacijos dalmuo, t. y. E = σ/ε; čia σ – statmenasis įtempis, ε – santykinė ilginė deformacija. atitikmenys: angl. coefficient …   Penkiakalbis aiškinamasis metrologijos terminų žodynas

  • module d’Young — Jungo modulis statusas T sritis fizika atitikmenys: angl. Yong’s modulus vok. Youngscher Modul, m rus. модуль Юнга, m pranc. module d’Young, m; module d’élasticité d’Young, m …   Fizikos terminų žodynas

  • Module d'élasticité — Module de Young Le module de Young ou module d élasticité (longitudinale) ou encore module de traction est la constante qui relie la contrainte de traction (ou de compression) et la déformation pour un matériau élastique isotrope. Le physicien… …   Wikipédia en Français

  • module — [ mɔdyl ] n. m. • 1547; lat. modulus, de modus « mesure » 1 ♦ Archit. Unité de mesure adoptée pour déterminer les proportions des membres d architecture. Le module des architectes grecs était le demi diamètre du fût de colonne à sa base. Par ext …   Encyclopédie Universelle

  • Module (mathématiques) — Module Cette page d’homonymie répertorie les différents sujets et articles partageant un même nom …   Wikipédia en Français

  • Module d'élasticité à la compression isostatique — Module d élasticité isostatique Le module d élasticité isostatique[1] ( bulk modulus en anglais) est la constante qui relie la contrainte au taux de déformation d un matériau isotrope soumis à une compression isostatique. Généralement noté K, il… …   Wikipédia en Français

  • Module d'élasticité isostatique — Le module d élasticité isostatique[1] (bulk modulus en anglais) est la constante qui relie la contrainte au taux de déformation d un matériau isotrope soumis à une compression isostatique. Généralement noté K (B en anglais), il permet d exprimer… …   Wikipédia en Français

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”