- Potentiel interatomique
-
Le potentiel interatomique est un modèle d'énergie potentielle servant à décrire l'interaction entre atomes.
Sommaire
Profil du potentiel
Attraction à grande distance
En dehors des gaz rares, les atomes à température ambiante s'associent spontanément pour former des molécules ou des cristaux. Il y a donc une force qui attire certains atomes entre eux. Cette force est conservative, et on peut donc lui associer une énergie potentielle, qu'on appelle souvent « potentiel » par abus de langage. L'énergie d'un système baisse lorsqu'il est plus stable ; par convention, on fixe l'énergie égale à zéro lorsque les atomes sont très éloignés (« à l'infini »).
La loi régissant cette force d'attraction dépend des associations d'atomes. Elle est particulièrement simple dans le cas d'ions de charge opposée : il s'agit de la force de Coulomb, ou force électrostatique. Dans ce cas précis, si r est la distance entre les ions et q+ et q- leur charge respective, alors l'intensité de la force vaut
et l'énergie potentielle est le potentiel électrostatique
Le profil exact du potentiel est différent dans les autres cas (liaison covalente, liaison métallique), mais reste du même ordre de grandeur.
Répulsion à courte distance
À courte distance, les atomes se repoussent en raison d'un effet purement quantique, le principe d'exclusion de Pauli, qui empêche l'interpénétration mutuelle des nuages électroniques de deux atomes. Comme précédemment, par convention, l'énergie associée à cette force est nulle à l'infini. Cette énergie tend vers l'infini lorsque la distance r tend vers 0
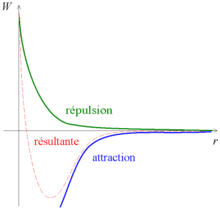
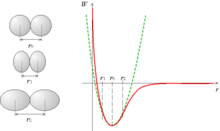
Profil résultant
Potentiel interatomique : somme d'une attraction et d'une répulsion
Le potentiel est la somme des deux contributions précédentes : aux valeurs élevées de r, c'est l'attraction qui prend le pas ; puis, aux faibles valeurs de r, l'énergie de répulsion croît plus vite que l'énergie d'attraction ne décroît. On a donc une courbe qui tend vers l'infini vers zéro, qui décroît jusqu'un minimum, puis croît en tendant vers zéro vers l'infini.
Le cas des gaz rares
En réalité, les gaz rares ne constituent pas une exception à cette description : les très faibles interactions mutuelles des atomes de gaz rare sont assez bien décrites par le potentiel de Lennard-Jones. Simplement, à température ambiante, le puits de potentiel n'est pas assez profond pour qu'il se forme des molécules stables.
Exemples de potentiels interatomiques
- Potentiel de Morse
- Potentiel de Lennard-Jones
- Potentiel de Stillinger-Weber
- Potentiel de Buckingham
Calcul de propriétés physiques
Ce profil de potentiel permet d'expliquer un certain nombre de propriétés de la matière.
Distances interatomiques, structure cristalline
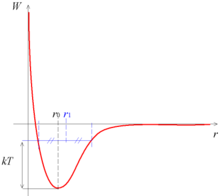
La courbe de potentiel présente un minimum en r0. Lorsquele système est à son minimum d'énergie (à la température du zéro absolu), la distance entre les atomes est donc r0, qui est de l'ordre de l'ångström.
Propriétés élastiques
Force de rappel à potentiel quasi-quadratiqueArticle détaillé : Déformation élastique.Lorsque l'on éloigne ou rapproche les atomes, on augmente l'énergie du système. On a donc une force de rappel qui ramène les atomes vers une distance r0.
Autour de r0, on peut faire un développement limité de la courbe, et donc « remplacer » localement la courbe par une parabole. Par approximation, l'énergie est donc en r2, la force de rappel est donc linéaire.
Dilatation et sublimation
Dissymétrie du potentiel et dilatationLorsque la température s'élève, les atomes vibrent entre eux. L'énergie mécanique associée à la température est kT, k étant la constante de Boltzmann et T la température absolue.
La courbe étant dissymétrique par rapport à r0, la distance moyenne entre les atomes augmente avec la température. Ceci explique la dilatation.
L'énergie du minimum r0 détermine la température de sublimation : lorsque kT est égal à l'opposé de cette énergie, l'énergie du système est nulle et la position moyenne est donc à l'infini, les atomes se dispersent spontanément.
Voir aussi
Articles connexes
Wikimedia Foundation. 2010.
