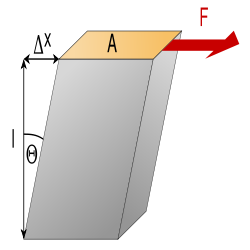
Module de cisaillement

Module de cisaillement: Schéma de principe du cisaillement.

En résistance des matériaux, le module de cisaillement, aussi appelé module de glissement, module de Coulomb ou second coefficient de Lamé, est une grandeur physique propre à chaque matériau et qui intervient dans la caractérisation des déformations causées par des efforts de cisaillement.

La définition du module de cisaillement $G$ est :
$G \ \stackrel{\mathrm{def}}{=}\ \frac {\tau_{xy}} {\gamma_{xy}} = \frac{F/A}{\Delta x/l} = \frac{F l}{A \Delta x}$
où (cf. image ci-contre) :

$τ x y = F / A$ est la contrainte de cisaillement ;

$F$ est la force ;

$A$ est l'aire sur laquelle la force agit ;

$γ x y = Δ x / l = tan θ$ est le déplacement latéral relatif, et $θ$ est l'écart à l'angle droit ;

$Δ x$ est le déplacement latéral ;

$l$ est l'épaisseur.

Le module de cisaillement a la dimension d'une contrainte et est généralement exprimé en GPa (gigapascals) ou en newtons par millimètre carré.
À titre d'exemple, le module de cisaillement de l'acier vaut environ 81 000 N/mm² soit 81 GPa.

Dans le cas de matériaux isotropes, il est relié au module d'élasticité $E$ et au coefficient de Poisson $ν$ par l'expression :
$G = \frac {E}{2(1+\nu)}$ .
Voir aussi

Module d'élasticité

Coefficient de Poisson

Viscoanalyseur

Cisaillage

v · Module de Young ( $E$ ) • Module de cisaillement ( $G$ ) • Module de compression ( $K$ ) • Premier coefficient de Lamé ( $λ$ ) • Coefficient de Poisson ( $ν$ ) • Module d'onde de compression ( $M$ , P-wave modulus)

Formules de conversion

Les propriétés élastiques des matériaux homogènes, isotropes et linéaires sont déterminées de manière unique par deux modules quelconques parmi ceux-ci. Ainsi, on peut calculer chacun à partir de deux d'entre eux en utilisant ces formules.

$(\lambda,\,G)$ $(E,\,G)$ $(K,\,\lambda)$ $(K,\,G)$ $(\lambda,\,\nu)$ $(G,\,\nu)$ $(E,\,\nu)$ $(K,\, \nu)$ $(K,\,E)$ $(M,\,G)$

$K=\,$ $\lambda+ \tfrac{2G}{3}$ $\tfrac{EG}{3(3G-E)}$ $\tfrac{\lambda(1+\nu)}{3\nu}$ $\tfrac{2G(1+\nu)}{3(1-2\nu)}$ $\tfrac{E}{3(1-2\nu)}$ $M - \tfrac{4G}{3}$

$E=\,$ $\tfrac{G(3\lambda + 2G)}{\lambda + G}$ $\tfrac{9K(K-\lambda)}{3K-\lambda}$ $\tfrac{9KG}{3K+G}$ $\tfrac{\lambda(1+\nu)(1-2\nu)}{\nu}$ $2G(1+\nu)\,$ $3K(1-2\nu)\,$ $\tfrac{G(3M-4G)}{M-G}$

$\lambda=\,$ $\tfrac{G(E-2G)}{3G-E}$ $K-\tfrac{2G}{3}$ $\tfrac{2 G \nu}{1-2\nu}$ $\tfrac{E\nu}{(1+\nu)(1-2\nu)}$ $\tfrac{3K\nu}{1+\nu}$ $\tfrac{3K(3K-E)}{9K-E}$ $M - 2G\,$

$G=\,$ $\tfrac{3(K-\lambda)}{2}$ $\tfrac{\lambda(1-2\nu)}{2\nu}$ $\tfrac{E}{2(1+\nu)}$ $\tfrac{3K(1-2\nu)}{2(1+\nu)}$ $\tfrac{3KE}{9K-E}$

$\nu=\,$ $\tfrac{\lambda}{2(\lambda + G)}$ $\tfrac{E}{2G}-1$ $\tfrac{\lambda}{3K-\lambda}$ $\tfrac{3K-2G}{2(3K+G)}$ $\tfrac{3K-E}{6K}$ $\tfrac{M - 2G}{2M - 2G}$

$M=\,$ $\lambda+2G\,$ $\tfrac{G(4G-E)}{3G-E}$ $3K-2\lambda\,$ $K+\tfrac{4G}{3}$ $\tfrac{\lambda(1-\nu)}{\nu}$ $\tfrac{2G(1-\nu)}{1-2\nu}$ $\tfrac{E(1-\nu)}{(1+\nu)(1-2\nu)}$ $\tfrac{3K(1-\nu)}{1+\nu}$ $\tfrac{3K(3K+E)}{9K-E}$

Portail de la physique

Portail des sciences des matériaux

Catégorie :
Mécanique des milieux continus

Formules de conversion
Les propriétés élastiques des matériaux homogènes, isotropes et linéaires sont déterminées de manière unique par deux modules quelconques parmi ceux-ci. Ainsi, on peut calculer chacun à partir de deux d'entre eux en utilisant ces formules.
	$(\lambda,\,G)$	$(E,\,G)$	$(K,\,\lambda)$	$(K,\,G)$	$(\lambda,\,\nu)$	$(G,\,\nu)$	$(E,\,\nu)$	$(K,\, \nu)$	$(K,\,E)$	$(M,\,G)$
$K=\,$	$\lambda+ \tfrac{2G}{3}$	$\tfrac{EG}{3(3G-E)}$			$\tfrac{\lambda(1+\nu)}{3\nu}$	$\tfrac{2G(1+\nu)}{3(1-2\nu)}$	$\tfrac{E}{3(1-2\nu)}$			$M - \tfrac{4G}{3}$
$E=\,$	$\tfrac{G(3\lambda + 2G)}{\lambda + G}$		$\tfrac{9K(K-\lambda)}{3K-\lambda}$	$\tfrac{9KG}{3K+G}$	$\tfrac{\lambda(1+\nu)(1-2\nu)}{\nu}$	$2G(1+\nu)\,$		$3K(1-2\nu)\,$		$\tfrac{G(3M-4G)}{M-G}$
$\lambda=\,$		$\tfrac{G(E-2G)}{3G-E}$		$K-\tfrac{2G}{3}$		$\tfrac{2 G \nu}{1-2\nu}$	$\tfrac{E\nu}{(1+\nu)(1-2\nu)}$	$\tfrac{3K\nu}{1+\nu}$	$\tfrac{3K(3K-E)}{9K-E}$	$M - 2G\,$
$G=\,$			$\tfrac{3(K-\lambda)}{2}$		$\tfrac{\lambda(1-2\nu)}{2\nu}$		$\tfrac{E}{2(1+\nu)}$	$\tfrac{3K(1-2\nu)}{2(1+\nu)}$	$\tfrac{3KE}{9K-E}$
$\nu=\,$	$\tfrac{\lambda}{2(\lambda + G)}$	$\tfrac{E}{2G}-1$	$\tfrac{\lambda}{3K-\lambda}$	$\tfrac{3K-2G}{2(3K+G)}$					$\tfrac{3K-E}{6K}$	$\tfrac{M - 2G}{2M - 2G}$
$M=\,$	$\lambda+2G\,$	$\tfrac{G(4G-E)}{3G-E}$	$3K-2\lambda\,$	$K+\tfrac{4G}{3}$	$\tfrac{\lambda(1-\nu)}{\nu}$	$\tfrac{2G(1-\nu)}{1-2\nu}$	$\tfrac{E(1-\nu)}{(1+\nu)(1-2\nu)}$	$\tfrac{3K(1-\nu)}{1+\nu}$	$\tfrac{3K(3K+E)}{9K-E}$

Contenu soumis à la licence CC-BY-SA. Source : Article Module de cisaillement de Wikipédia en français (auteurs)

Игры ⚽ Нужно сделать НИР?

Regardez d'autres dictionnaires:

module de cisaillement — šlyties modulis statusas T sritis fizika atitikmenys: angl. modulus of rigidity; shear modulus vok. Gleitmodul, m; Schermodul, m; Schubmodul, m rus. модуль сдвига, m pranc. module de cisaillement, m; module de rigidité, m; module d’élasticité au… … Fizikos terminų žodynas
module de cisaillement — šlyties modulis statusas T sritis Standartizacija ir metrologija apibrėžtis Liestinio įtempio ir santykinės šlyjamosios deformacijos dalmuo, t. y. G = τ/γ ; čia τ – liestinis įtempis, γ – santykinė šlyjamoji deformacija. atitikmenys: angl.… … Penkiakalbis aiškinamasis metrologijos terminų žodynas
Module De Young — Le module de Young ou module d élasticité (longitudinale) ou encore module de traction est la constante qui relie la contrainte de traction (ou de compression) et la déformation pour un matériau élastique isotrope. Le physicien britannique Thomas … Wikipédia en Français
Module d'Young — Module de Young Le module de Young ou module d élasticité (longitudinale) ou encore module de traction est la constante qui relie la contrainte de traction (ou de compression) et la déformation pour un matériau élastique isotrope. Le physicien… … Wikipédia en Français
Module d'élasticité — Module de Young Le module de Young ou module d élasticité (longitudinale) ou encore module de traction est la constante qui relie la contrainte de traction (ou de compression) et la déformation pour un matériau élastique isotrope. Le physicien… … Wikipédia en Français
Module de young — Le module de Young ou module d élasticité (longitudinale) ou encore module de traction est la constante qui relie la contrainte de traction (ou de compression) et la déformation pour un matériau élastique isotrope. Le physicien britannique Thomas … Wikipédia en Français
Module de relaxation — En rhéologie, le module de relaxation permet de rendre compte de la relaxation de contrainte après une déformation. Écriture générale d une contrainte La contrainte σ à un temps t ne dépend pour un fluide newtonien que du taux de déformation à ce … Wikipédia en Français
Module de Young — Le module de Young ou module d élasticité (longitudinale) ou encore module de traction est la constante qui relie la contrainte de traction (ou de compression) et la déformation pour un matériau élastique isotrope. Le physicien britannique Thomas … Wikipédia en Français
Module d'élasticité isostatique — Le module d élasticité isostatique[1] (bulk modulus en anglais) est la constante qui relie la contrainte au taux de déformation d un matériau isotrope soumis à une compression isostatique. Généralement noté K (B en anglais), il permet d exprimer… … Wikipédia en Français
module d’élasticité au cisaillement — šlyties modulis statusas T sritis fizika atitikmenys: angl. modulus of rigidity; shear modulus vok. Gleitmodul, m; Schermodul, m; Schubmodul, m rus. модуль сдвига, m pranc. module de cisaillement, m; module de rigidité, m; module d’élasticité au… … Fizikos terminų žodynas

Dictionnaires et Encyclopédies sur 'Academic'

Module de cisaillement

Voir aussi

Regardez d'autres dictionnaires:

Share the article and excerpts

Dictionnaires et Encyclopédies sur 'Academic'

Wikipédia en Français

Module de cisaillement

Voir aussi

Regardez d'autres dictionnaires:

Share the article and excerpts

Direct link