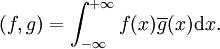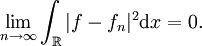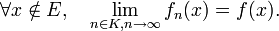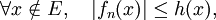- Carré intégrable
-
Carré sommable
En mathématiques, on dit qu'une fonction f mesurable de
 dans
dans  est de carré sommable lorsque la quantité
est de carré sommable lorsque la quantitéest un nombre fini.
Sommaire
Définitions précises
L'ensemble de ces fonctions, qui peuvent ne pas être définies sur un ensemble de mesure nulle, forme un espace vectoriel
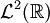 , qu'on peut munir d'une forme bilinéaire semi-définie hermitienne définie par
, qu'on peut munir d'une forme bilinéaire semi-définie hermitienne définie parLa semi-norme correspondante est :
Le noyau de la semi-norme est l'ensemble des fonctions négligeables, c'est-à-dire nulles presque partout.
Le quotient de
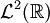 par l'espace des fonctions négligeables est l'espace
par l'espace des fonctions négligeables est l'espace 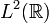 . C'est un espace de classes de fonctions : deux fonctions sont dans la même classe si elles sont égales presque partout, c'est-à-dire en dehors d'un ensemble de mesure nulle. Si f est dans
. C'est un espace de classes de fonctions : deux fonctions sont dans la même classe si elles sont égales presque partout, c'est-à-dire en dehors d'un ensemble de mesure nulle. Si f est dans 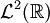 , notons pour le moment [f] la classe de f.
, notons pour le moment [f] la classe de f.On munit l'espace
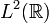 d'une structure d'espace de Hilbert à l'aide du produit scalaire suivant :
d'une structure d'espace de Hilbert à l'aide du produit scalaire suivant :La norme correspondante est :
Il est immédiat que ces intégrales ne dépendent pas du représentant qu'on a choisi pour la classe de f ou de g.
Simplifications en passant aux fonctions définies presque partout
Sauf mention particulière, on utilise surtout l'espace
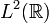 , et on se dispense de faire la différence entre fonction de carré sommable et fonction de carré sommable modulo les fonctions négligeables. Cet abus est justifié dans l'immense majorité des cas, et on peut donc simplifier les définitions comme suit: l'espace
, et on se dispense de faire la différence entre fonction de carré sommable et fonction de carré sommable modulo les fonctions négligeables. Cet abus est justifié dans l'immense majorité des cas, et on peut donc simplifier les définitions comme suit: l'espace 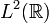 des fonctions de carré sommable (définies presque partout) est l'ensemble des fonctions mesurables définies presque partout sur
des fonctions de carré sommable (définies presque partout) est l'ensemble des fonctions mesurables définies presque partout sur  , telles que le carré de leur module soit intégrable sur / R. C'est un espace de Hilbert, une fois qu'on le munit du produit scalaire
, telles que le carré de leur module soit intégrable sur / R. C'est un espace de Hilbert, une fois qu'on le munit du produit scalaireQuelques propriétés
Une suite de fonctions fn définies presque partout sur
 et de carré sommable converge dans
et de carré sommable converge dans 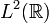 vers une limite f si
vers une limite f siOn dit alors qu'elle converge en moyenne quadratique. La convergence en moyenne quadratique n'implique pas en général la convergence presque partout. Cependant, on peut extraire une sous-suite presque partout convergente d'une suite convergeant en moyenne quadratique. En d'autres termes, si
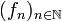 converge vers f en moyenne quadratique, on peut trouver une partie infinie K de
converge vers f en moyenne quadratique, on peut trouver une partie infinie K de 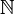 et un ensemble E de mesure nulle tels que
et un ensemble E de mesure nulle tels queLe théorème de convergence dominée de Lebesgue fournit une condition suffisante de convergence en moyenne quadratique : soit fn une suite de fonctions de carré sommable. Supposons qu'il existe une fonction h de carré sommable et un ensemble E de mesure nulle tels que
et que fn converge presque partout vers une limite f. Alors f est de carré sommable et la suite fn converge en moyenne quadratique vers f.
Les fonctions de carré sommable en physique
En physique quantique, une fonction d'onde
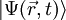 associée à une particule est de carré sommable. Physiquement, en effet, le carré du module de la fonction d'onde
associée à une particule est de carré sommable. Physiquement, en effet, le carré du module de la fonction d'onde 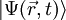 est une densité de probabilité de présence de la particule au point
est une densité de probabilité de présence de la particule au point 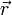 et à l'instant t. Par conséquent, l'intégrale de ce carré vaut 1, puisque la particule se trouve quelque part dans l'espace. En termes plus mathématiques, une fonction d'onde est de norme 1 dans l'espace des fonctions de carré sommable.
et à l'instant t. Par conséquent, l'intégrale de ce carré vaut 1, puisque la particule se trouve quelque part dans l'espace. En termes plus mathématiques, une fonction d'onde est de norme 1 dans l'espace des fonctions de carré sommable.- Portail des mathématiques
Catégorie : Théorie de l'intégration
Wikimedia Foundation. 2010.

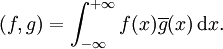
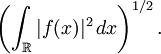
![([f],[g]) = \int_{-\infty}^{+\infty} f(x)\overline{g}(x)\mathrm{d}x](/pictures/frwiki/97/ac83e80982bd945a2405495f2a88f059.png)
![\|[f]\|_{L^2}=\left(\int_\R |f(x)|^2\, dx\right)^{1/2}.](/pictures/frwiki/49/1d07bd4a0f6675e1a93b613caba4f300.png)