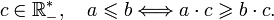Inegalite (mathematiques)
- Inegalite (mathematiques)
-
Inégalité (mathématiques)
Wikimedia Foundation.
2010.
Contenu soumis à la licence CC-BY-SA. Source : Article Inegalite (mathematiques) de Wikipédia en français (auteurs)
Regardez d'autres dictionnaires:
Inégalité (mathématiques) — Pour les articles homonymes, voir inégalité. En mathématiques, une inégalité est un énoncé permettant de comparer la taille, ou l ordre de deux objets (dans le cas où ils seraient égaux, on a une égalité) La notation a < b signifie que a est… … Wikipédia en Français
Inegalite — Inégalité Cette page d’homonymie répertorie les différents sujets et articles partageant un même nom … Wikipédia en Français
Inégalité socio-économique — Inégalité Cette page d’homonymie répertorie les différents sujets et articles partageant un même nom … Wikipédia en Français
Inégalité stricte — En mathématiques, une inégalité stricte est une relation entre deux éléments comparables qui exclut le cas d égalité, au contraire d une inégalité large. Plus généralement, l adjectif « strict » et l adverbe « strictement »… … Wikipédia en Français
Inégalité — Cette page d’homonymie répertorie les différents sujets et articles partageant un même nom. Sur les autres projets Wikimedia : « Inégalité », sur le Wiktionnaire (dictionnaire universel) Inégalités de revenu Inégalités de richesse… … Wikipédia en Français
Inegalite de Cauchy-Schwarz — Inégalité de Cauchy Schwarz Pour les articles homonymes, voir Cauchy et Schwarz. En mathématiques, l inégalité de Cauchy Schwarz, aussi appelée inégalité de Schwarz[1], ou encore inégalité de Cauchy Bunyakovski Schwarz[2], se rencontre dans de… … Wikipédia en Français
Inégalité De Cauchy-Schwarz — Pour les articles homonymes, voir Cauchy et Schwarz. En mathématiques, l inégalité de Cauchy Schwarz, aussi appelée inégalité de Schwarz[1], ou encore inégalité de Cauchy Bunyakovski Schwarz[2], se rencontre dans de nombreux doma … Wikipédia en Français
Inégalité de cauchy-schwarz — Pour les articles homonymes, voir Cauchy et Schwarz. En mathématiques, l inégalité de Cauchy Schwarz, aussi appelée inégalité de Schwarz[1], ou encore inégalité de Cauchy Bunyakovski Schwarz[2], se rencontre dans de nombreux doma … Wikipédia en Français
Inegalite de Jensen — Inégalité de Jensen En mathématiques, en analyse, l’inégalité de Jensen est une relation utile et très générale concernant les fonctions convexes, due au mathématicien danois Johan Jensen et dont il donna la preuve en 1906[1]. On peut l écrire de … Wikipédia en Français
Inégalité De Jensen — En mathématiques, en analyse, l’inégalité de Jensen est une relation utile et très générale concernant les fonctions convexes, due au mathématicien danois Johan Jensen et dont il donna la preuve en 1906[1]. On peut l écrire de deux manières … Wikipédia en Français
 Pour les articles homonymes, voir inégalité.
Pour les articles homonymes, voir inégalité.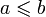 avec
avec 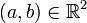
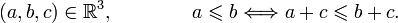
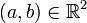 et
et 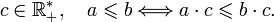
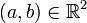 et
et