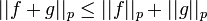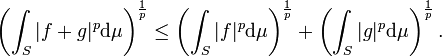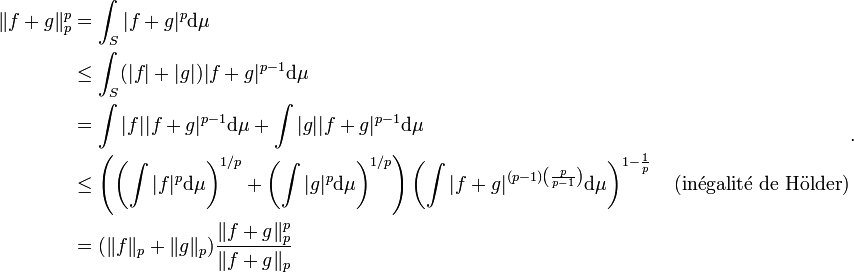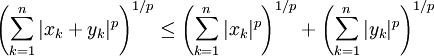Inégalité De Minkowski
- Inégalité De Minkowski
-
Inégalité de Minkowski
En mathématiques, l'inégalité de Minkowski établit que les espaces Lp sont des espaces vectoriels normés. Elles sont nommées ainsi en l'honneur de Hermann Minkowski.
Énoncé
Soit (S,μ) un espace mesuré et soit 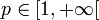 . Alors pour tout (
. Alors pour tout (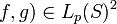 , on a
, on a
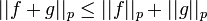
c'est-à-dire
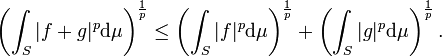
Démonstration
L'espace L_p(S) étant un espace vectoriel, f + g est aussi dans Lp(S). Si | | f + g | | p vaut zéro, or l'inégalité est vérifiée. On suppose maintenant que | | f + g | | p > 0.
On a
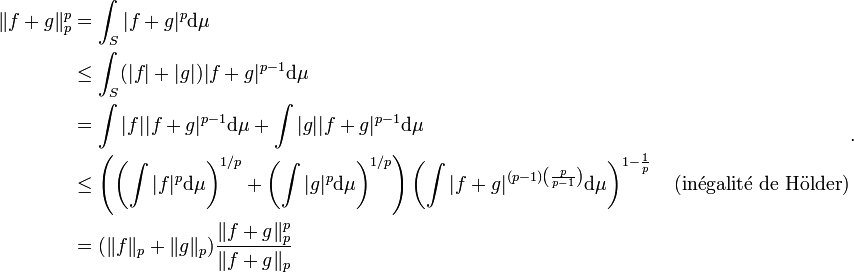
En multipliant des deux côtés par ( | | f + g | | p) / ( | | f + g | | p)p, on obtient l'inégalité recherchée.
En d'autres termes, cela signifie que 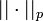 vérifie l'inégalité triangulaire.
vérifie l'inégalité triangulaire.
Si p > 1, il y a égalité si, et seulement si, f et g sont positivement liées (c'est-à-dire s'il existe 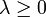 tel que f = λg).
tel que f = λg).
À l'instar des inégalités de Hölder, les inégalités de Minkowski peuvent être spécialisés pour les vecteurs ou même les séries:
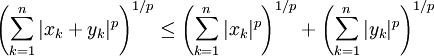
Ici, n peut être un entier naturel ou peut être égal à  , et les xk et yk sont des réels ou des complexes. Ces inégalités se déduisent de la première en utilisant une mesure de dénombrement.
, et les xk et yk sont des réels ou des complexes. Ces inégalités se déduisent de la première en utilisant une mesure de dénombrement.
Voir aussi
 Portail des mathématiques
Portail des mathématiques
Catégories : Géométrie euclidienne | Théorie de la mesure | Inégalité | Algèbre bilinéaire
Wikimedia Foundation.
2010.
Contenu soumis à la licence CC-BY-SA. Source : Article Inégalité De Minkowski de Wikipédia en français (auteurs)
Regardez d'autres dictionnaires:
Inegalite de Minkowski — Inégalité de Minkowski En mathématiques, l inégalité de Minkowski établit que les espaces Lp sont des espaces vectoriels normés. Elles sont nommées ainsi en l honneur de Hermann Minkowski. Énoncé Soit (S,μ) un espace mesuré et soit . Alors pour… … Wikipédia en Français
Inégalité de minkowski — En mathématiques, l inégalité de Minkowski établit que les espaces Lp sont des espaces vectoriels normés. Elles sont nommées ainsi en l honneur de Hermann Minkowski. Énoncé Soit (S,μ) un espace mesuré et soit . Alors pour tout ( , on a … Wikipédia en Français
Inégalité de Minkowski — En mathématiques, l inégalité de Minkowski, ainsi nommée en l honneur de Hermann Minkowski, est l’inégalité triangulaire pour la norme des espaces Lp, établissant ainsi que ce sont des espaces vectoriels normés. Elle concerne également la norme… … Wikipédia en Français
inégalité de Minkowski — Minkovskio nelygybė statusas T sritis fizika atitikmenys: angl. Minkowski’s inequality vok. Minkowskische Ungleichung, f rus. неравенство Минковского, n pranc. inégalité de Minkowski, f … Fizikos terminų žodynas
Inegalite de Cauchy-Schwarz — Inégalité de Cauchy Schwarz Pour les articles homonymes, voir Cauchy et Schwarz. En mathématiques, l inégalité de Cauchy Schwarz, aussi appelée inégalité de Schwarz[1], ou encore inégalité de Cauchy Bunyakovski Schwarz[2], se rencontre dans de… … Wikipédia en Français
Inégalité De Cauchy-Schwarz — Pour les articles homonymes, voir Cauchy et Schwarz. En mathématiques, l inégalité de Cauchy Schwarz, aussi appelée inégalité de Schwarz[1], ou encore inégalité de Cauchy Bunyakovski Schwarz[2], se rencontre dans de nombreux doma … Wikipédia en Français
Inégalité de cauchy-schwarz — Pour les articles homonymes, voir Cauchy et Schwarz. En mathématiques, l inégalité de Cauchy Schwarz, aussi appelée inégalité de Schwarz[1], ou encore inégalité de Cauchy Bunyakovski Schwarz[2], se rencontre dans de nombreux doma … Wikipédia en Français
Inegalite de Holder — Inégalité de Hölder En analyse, l’inégalité de Hölder, du nom de Otto Hölder, est une inégalité fondamentale relative aux espaces Lp : soit S un espace mesuré, soient 1 ≤ p, q ≤ ∞ avec 1/p + 1/q = 1, soit f une fonction de Lp(S) et g dans… … Wikipédia en Français
Inégalité De Hölder — En analyse, l’inégalité de Hölder, du nom de Otto Hölder, est une inégalité fondamentale relative aux espaces Lp : soit S un espace mesuré, soient 1 ≤ p, q ≤ ∞ avec 1/p + 1/q = 1, soit f une fonction de Lp(S) et g dans Lq(S). Alors fg… … Wikipédia en Français
Inégalité de hölder — En analyse, l’inégalité de Hölder, du nom de Otto Hölder, est une inégalité fondamentale relative aux espaces Lp : soit S un espace mesuré, soient 1 ≤ p, q ≤ ∞ avec 1/p + 1/q = 1, soit f une fonction de Lp(S) et g dans Lq(S). Alors fg… … Wikipédia en Français
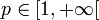 . Alors pour tout (
. Alors pour tout (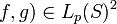 , on a
, on a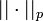 vérifie l'inégalité triangulaire.
vérifie l'inégalité triangulaire.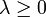 tel que f = λg).
tel que f = λg). , et les xk et yk sont des réels ou des complexes. Ces inégalités se déduisent de la première en utilisant une mesure de dénombrement.
, et les xk et yk sont des réels ou des complexes. Ces inégalités se déduisent de la première en utilisant une mesure de dénombrement.