Alembert

D’Alembert
Nom de naissance	Jean le Rond d’Alembert
Naissance	16 novembre 1717 Paris
Décès	29 octobre 1783 (à 65 ans) Paris
Nationalité	France
Profession(s)	Mathématicien et philosophe

Jean le Rond D'Alembert^[1],[2] ou Jean Le Rond d’Alembert^[3],[4], né le 16 novembre 1717 à Paris où il est mort le 29 octobre 1783, est un mathématicien, philosophe et encyclopédiste français.

Il est célèbre pour avoir dirigé l’Encyclopédie avec Denis Diderot jusqu’en 1757 et pour ses recherches en mathématiques sur les équations différentielles et les dérivées partielles.

Biographie

Enfance

Fruit d’un amour illégitime entre la célèbre femme de lettres et salonnière Claudine Guérin de Tencin et le chevalier Louis-Camus Destouches, commissaire d’artillerie, D’Alembert naît le 16 novembre 1717 à Paris. Le lendemain, il est abandonné par sa mère qui le fait porter par un serviteur sur les escaliers de la chapelle Saint-Jean-le-Rond attenant à la tour nord de Notre-Dame de Paris. Comme le veut la coutume, il est nommé du nom du saint protecteur de la chapelle et devient Jean Le Rond. Il est d’abord placé à l’hospice des Enfants-Trouvés, mais son père le retrouve rapidement et le place dans une famille d’adoption. Bien qu’il ne reconnaisse pas officiellement sa paternité, le chevalier Destouches veille secrètement à son éducation en lui accordant une pension et le visite quelquefois chez sa nourrice, madame Rousseau, la fameuse « vitrière » chez qui il vivra jusqu’à ses cinquante ans.

Études^[5]

À douze ans, il entra au collège des Quatre-Nations. Il y fit de brillantes études, obtint le baccalauréat en arts, puis suivit les cours de l’École de Droit. Il s’était d’abord inscrit sous le nom de Daremberg, puis il le change en D’Alembert, nom qu’il conservera toute sa vie. Refusant de s’inscrire au barreau, il entreprit des études de médecine, puis les abandonna également.

Premiers travaux scientifiques (1739-1746)

À 22 ans, en 1739, il présenta à l’Académie des Sciences, son premier travail en mathématiques sur des erreurs qu’il avait décelées dans l’Analyse démontrée, ouvrage publié en 1708 par Charles-René Reynaud avec lequel D’Alembert avait lui-même étudié les bases des mathématiques. Dès 1742, à 24 ans, il est nommé adjoint de la section d’Astronomie de l’Académie des sciences où son grand rival en mathématiques et en physique fut Alexis Clairaut. En 1743, il publia son célèbre Traité de Dynamique, qui dans l’histoire de la mécanique représente l’étape qu’il fallait franchir entre l’œuvre de Newton et celle de Lagrange. En 1746, il est élu associé géomètre.

Il entra à l’Académie de Berlin à 28 ans.

La suite de sa carrière à l’Académie des Sciences fut moins brillante. Nommé pensionnaire surnuméraire en 1756, ce n'est qu’en 1765, à 47 ans, qu’il devint pensionnaire.

L’homme de Lettres (1746-1757)

Ami de Voltaire et constamment mêlé aux controverses passionnées de ce temps, il était un habitué des salons parisiens, notamment ceux de Marie-Thérèse Geoffrin, de Marie du Deffand et de Julie de Lespinasse.

C’est là qu’il rencontra Denis Diderot, en 1746. L'année suivante, ils prennent conjointement la tête de L'Encyclopédie. En 1751, après cinq ans de travail de plus de deux cents contributeurs, paraissait le premier tome de l’encyclopédie dont D’Alembert rédigea le Discours préliminaire.

En 1754, D’Alembert est élu membre de l’Académie française, dont il deviendra le secrétaire perpétuel le 9 avril 1772. L'année 1754 voit également la parution de l’article « Genève » dans l’Encyclopédie, pour lequel il fut attaqué par Jean-Jacques Rousseau. Après une série de crises, la publication de l’Encyclopédie est suspendue de 1757 à 1759. D'Alembert, prudent, se retira de l’entreprise, en 1757, après s’être fâché avec Diderot.

Après 1757

Jusqu’à sa mort, il continua ses travaux scientifiques et disparut au faîte de sa célébrité, prenant ainsi une revanche éclatante sur sa naissance misérable.

Il quitta la maison familiale en 1765 pour vivre un amour platonique et difficile avec l’écrivaine Julie de Lespinasse, qui disparut en 1776.

Postérité

Nicolas de Condorcet en a fait l’éloge funèbre en 1783, soulignant ses apports scientifiques.

Son œuvre complète a été republiée en 1805 et en 1821-1822 mais les écrits scientifiques sont alors omis. Cette erreur n'est en cours de réparation que de nos jours avec la sortie en cours de ses Œuvres complètes aux éditions du CNRS^[6].

Son œuvre

L'Encyclopédie

En 1745, D’Alembert, qui était alors membre de l’Académie des sciences, est chargé par André Le Breton, d’abord sous la direction de Gua de Malves, de traduire de l’anglais en français le Cyclopaedia d’Ephraim Chambers. D’une simple traduction, le projet se transforma en la rédaction d’une œuvre originale et unique en son genre, l’Encyclopédie ou dictionnaire raisonné des sciences, des arts et des métiers. D’Alembert écrira le fameux Discours préliminaire ainsi que la plupart des articles sur les mathématiques et les sciences. Il rédigea (sous la signature O) ainsi près de 1700 articles, la plupart concernant les mathématiques au sens large^[7] mais baissa très sensiblement son niveau de participation à partir de 1762.

« Penser d’après soi » et « penser par soi-même », formules devenues célèbres, sont dues à D’Alembert ; on les trouvera dans le Discours préliminaire, Encyclopédie, tome 1, 1751. Ces formulations sont une reprise d’injonctions anciennes (Hésiode, Horace).

Le terme de Cacouac est inventé dans les années 1750 par les adversaires des philosophes des Lumières, en vue de ridiculiser plus particulièrement les auteurs de l’Encyclopédie

Mathématiques

Le théorème de D’Alembert

Dans le Traité de dynamique, il énonce le théorème de d'Alembert (aussi connu sous théorème de Gauss-d’Alembert) qui dit que tout polynôme de degré n à coefficients complexes possède exactement n racines dans (non nécessairement distinctes, il faut tenir compte du nombre de fois qu’une racine est répétée). Ce théorème ne sera démontré qu’au XIX^e siècle par Carl Friedrich Gauss. Louis de Broglie présente ce théorème ainsi : « On lui doit le théorème fondamental qui porte son nom et qui nous apprend que toute équation algébrique admet au moins une solution réelle ou imaginaire » (Réf. en bibliographie).

Critère de D’Alembert pour la convergence des séries numériques

Soit 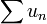une série à termes strictement positifs pour laquelle le rapport 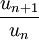tend vers une limite 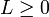. Alors :

• si L<1 : la série de terme général u_n converge.
• si L>1 : la série de terme général u_n diverge.
• si L=1 : on ne peut conclure.

Martingale de D’Alembert

À un jeu où l’on gagne le double de la mise avec une probabilité de 50 % (par exemple à la roulette, en jouant pair / impair, passe / manque), il propose la stratégie suivante :

• Miser une unité
• Si l’on gagne, se retirer
• Si l’on perd, miser le double (de quoi couvrir la perte antérieure et laisser un gain)
• continuer jusqu’à un gain… ou épuisement

Avec ce procédé, le jeu n’est pas forcément gagnant, mais on augmente ses chances de gagner (un peu) au prix d’une augmentation de la perte possible (mais plus rare). Par, exemple, si par malchance on ne gagne qu’à la dixième fois après avoir perdu 9 fois, il aura fallu miser et perdre 1+2+4+8+16+32+64+128+256+512 = 2¹⁰-1 unités, pour en gagner 1024, avec un solde final de seulement 1 ! Et il aura fallu être prêt à éventuellement supporter une perte de 1023, avec une probabilité faible (1/1024), mais non nulle. Même avec une richesse de départ infinie (?) et une durée de jeu sans limite, il faut encore faire face à l’éventualité que le jeu ne s’arrête jamais.

Enfin, il faut s’abstenir de jouer à nouveau après un gain, puisque cela a l’effet inverse à celui de la martingale (augmenter la probabilité de la perte).

Il existe d’autres types de martingales célèbres, qui toutes nourrissent le faux espoir d’un gain certain.

L’attribution de cette martingale à D’Alembert est néanmoins sujette à caution.

Dans la réalité la possibilité d'utiliser cette martingale est limitée par le plafonnement des mises par les casinos.

Astronomie

Il étudia le problème des trois corps et les équinoxes, dans le mémoire publié en 1749 sur la précession des équinoxes. Ce phénomène, dont la période est de 26 000 ans, avait été constaté par Hipparque dans l’Antiquité. Newton avait compris que la cause de ce phénomène résidait dans l’action des forces de gravitation sur le corps non rigoureusement sphérique qu’est le globe terrestre. Mais c’est à D’Alembert qu’il revint de pousser les calculs et d’obtenir des résultats numériques en accord avec l’observation. D’Alembert fit également progresser le difficile problème que constituait pour les astronomes l’explication du mouvement lunaire. En ce sens, il est le précurseur de la Mécanique céleste de Laplace.

D'Alembert travailla également sur le problème de l’aberration chromatique qui limitait la précision des lunettes astronomiques, en concurrence avec Alexis Claude Clairaut et avec Leonhard Euler. Il proposa de superposer plusieurs lentilles de forme et d'indice différent. Il fit également des avancées sur le problème des aberrations hors-axe^[8].

Physique

En 1743 dans le Traité de dynamique dans lequel il énonce le principe de la quantité de mouvement, qui est parfois appelé principe de d'Alembert.

« Si l’on considère un système de points matériels liés entre eux de manière que leurs masses acquièrent des vitesses respectives différentes selon qu’elles se meuvent librement ou solidairement, les quantités de mouvements gagnées ou perdues dans le système sont égales. »

Ce principe a servi de base au développement de la mécanique analytique. D’Alembert considère le cas général d’un système mécanique qui évolue en restant soumis à des liaisons; il montre que les forces de liaison s’équilibrant, il doit y avoir équivalence entre les forces réelles qui impriment son mouvement au système et les forces qu’il faudrait mettre en œuvre si les liaisons n’existaient pas. Ce faisant, il éliminait les forces de liaison, dont les formes sont généralement inconnues, et, ramenait, d’une certaine manière, le problème de la dynamique envisagé à une question d’équilibre, c’est-à-dire de statique. Cela permettait de ramener tout problème de statique à l’application d’un principe général, qu’on nommait alors le « principe des vitesses virtuelles ». Ce faisant, D’Alembert jetait les bases sur lesquelles Lagrange allait bâtir l’édifice grandiose de la Mécanique céleste.

Il étudia aussi les équations différentielles et les équations à dérivées partielles.

En hydrodynamique, on lui doit d’avoir démontré le paradoxe qui porte son nom : il montra que, d’après les solutions les plus simples des équations hydrodynamiques, un corps devrait pouvoir progresser dans un fluide sans éprouver aucune résistance ou, ce qui revient au même, qu’une pile de pont plongée dans le cours d’un fleuve ne devait subir de sa part aucune poussée. C’était obtenir un résultat contraire à l’intuition et à l’expérience. Il fallut attendre la théorie des sillages, qui substitue aux solutions continues simples de l’hydrodynamique, des solutions de surfaces de discontinuités et mouvements tourbillonnaires, pour venir à bout de cette difficulté qu’avait soulevée D’Alembert.

Il est également à l’origine de l’équation de d'Alembert.

Philosophie

D'Alembert découvre la philosophie au collège janséniste des Quatre-Nations. Il s’intéresse également aux langues anciennes et à la théologie. Il commente entre autres l’Épître de saint Paul aux Romains). À la sortie du collège, il laisse définitivement de côté la théologie et se lance dans des études de droit, de médecine et de mathématiques. De ses premières années d’études, il conservera une tradition cartésienne qui, intégrée aux conceptions newtoniennes, ouvrira la voie au rationalisme scientifique moderne.

C’est l’Encyclopédie, à laquelle il collaborera avec Diderot et d’autres penseurs de son temps, qui lui donnera l’occasion de formaliser sa pensée philosophique. Le Discours préliminaire de l’Encyclopédie, inspiré de la philosophie empiriste de John Locke et publié en tête du premier volume (1751), est souvent considéré, et avec raison, comme un véritable manifeste de la philosophie des Lumières. Il y affirme l’existence d’un lien direct entre le progrès des connaissances et le progrès social.

Contemporain du siècle des Lumières, déterministe et athée (tout du moins déiste), D’Alembert fut l’un des protagonistes, ainsi que son ami Voltaire, de la lutte contre l’absolutisme religieux et politique qu’il dénonce dans les nombreux articles philosophiques qu’il écrivit pour l’Encyclopédie. La compilation de ses analyses spirituelles de chaque domaine de la connaissance humaine traité par l’Encyclopédie, constituent une véritable philosophie des sciences.

Dans Philosophie expérimentale, D’Alembert définit ainsi la philosophie : « La philosophie n’est autre chose que l’application de la raison aux différents objets sur lesquels elle peut s’exercer. »

D’Alembert est représenté dans l’Entretien entre d’Alembert et Diderot, le Rêve de d’Alembert et la Suite de l’entretien (été 1769) par Diderot.

Musique

D’Alembert est considéré comme un théoricien de la musique, en particulier dans Éléments de musique. Une controverse l’opposa à ce sujet à Jean-Philippe Rameau.

Étudiant la vibration des cordes, il parvint à montrer que le mouvement d’une corde vibrante est représenté par une équation aux dérivées partielles, et a indiqué la solution générale de cette équation. Cette équation des cordes vibrantes a été le premier exemple de l’équation des ondes. Cela fait de D’Alembert, l’un des fondateurs de la physique mathématique. Ses travaux ont été à l’origine de polémiques fécondes, lorsque Euler, à la suite de Bernoulli, eut donné sous la forme d’une série trigonométrique, une solution de l’équation des cordes vibrantes qui semblait totalement différer de celle de D’Alembert. Il a résulté de la discussion que la solution trigonométrique pouvait s’adapter à la représentation d’une forme initiale arbitraire de la corde.

Œuvres

• Mémoire sur le calcul intégral’' (1739), première œuvre publiée,
• Traité de dynamique (1743),
• Traité de l’équilibre et du mouvement des fluides (1744),
• Réflexions sur la cause générale des vents (1746),
• Recherches sur les cordes vibrantes (1747),
• Recherches sur la précession des équinoxes et sur la nutation de l’axe de la terre (1749),
• Éléments de musique (1752),
• Mélanges de littérature et de philosophie (2 tomes 1753, 5 tomes 1759-1767),
• Essai sur les éléments de philosophie (1759)
• Éloges lus dans les séances publiques de l’Académie française (1779)
• Opuscules mathématiques (8 tomes 1761-1780)
• Œuvres complètes, Éditions CNRS, 2002. (ISBN 2-271060133)
• Encyclopédie ou Dictionnaire raisonné des sciences, des arts et des métiers, Flammarion, 1993 (ISBN 2-080704265)
• Opuscules mathématiques, Paris, David, Briasson, Jombert, 1761-1780
• Réflexions sur la cause générale des vents, Paris, David l’aîné, 1747
• Traité de dynamique, Paris, David, 1758
• Traité de l’équilibre et du mouvement des fluides : pour servir de suite au Traité de dynamique, Paris, David, 1749
• Trois Mois à la cour de Frédéric, Paris, C. Lévy, 1886
• Correspondance avec Frédéric le Grand, ed. Preuss, Berlin, Duncker 1854, e.a.

Bibliographie

• Joseph Bertrand, d’Alembert, texte disponible en ligne sur le projet Gutenberg.
• Louis de Broglie, Un mathématicien, homme de lettres : d’Alembert, L’Encyclopédie et le progrès des sciences et des techniques, Centre International de synthèse, Paris, PUF, 1952, p. 1-9
• La formation de D'Alembert. Recherche sur Diderot et sur l’Encyclopédie, 2008, n°38.
• D'Alembert : mathématicien des Lumières. Revue « Pour la science » (ISSN 1298-6879), 2009, n^o 39. (ISBN 978-2-84245-095-3)

Notes

Liens externes

• Comité D'Alembert : Édition des œuvres complètes
• Notice biographique de l’Academie francaise

• Portail de la littérature
• Portail de la philosophie
• Portail des mathématiques
• Portail du XVIII^e siècle
• Portail des Lumières