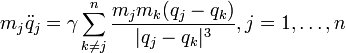Problème des trois corps

Le problème à N corps consiste à résoudre les équations du mouvement de Newton de N corps interagissant gravitationnellement, connaissant leurs masses ainsi que leurs positions et vitesses initiales.

Il s'agit d'un problème mathématique fondamental pour l'astronomie classique, c’est-à-dire dans le cas où les effets de la théorie de la relativité générale d'Einstein peuvent être négligés : vitesses des corps petites devant la vitesse de la lumière dans le vide, et champs de gravitation faibles, ce qui est essentiellement le cas dans le système solaire.

Le problème à N corps se pose également dans le cadre de la relativité générale ; son étude y est encore plus difficile que dans le cadre newtonien.

Sommaire 1 Formulation mathématique 2 Problème à deux corps ou mouvement keplerien 3 Problème à N corps 4 Remarque sur le problème à trois corps 5 Annexes 5.1 Articles connexes 5.2 Bibliographie 5.2.1 Initiation 5.2.2 Textes plus techniques 5.2.2.1 Les modernes 5.2.2.2 Les classiques 5.2.3 Analyse numérique 5.2.4 Quelques travaux récents 5.3 Références

Formulation mathématique

Le problème à N corps est modélisé par une équation différentielle. Étant donné les valeurs initiales des positions q_j(0) et des vitesses 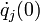des N particules (j = 1,...,N) avec 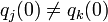pour tout j et k distincts, il s'agit de trouver une solution du système du second-ordre

où 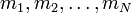sont des constantes représentant les masses des N particules, et 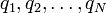sont leurs vecteurs position (à trois dimensions) dépendant du temps t. Cette équation est simplement la seconde loi du mouvement de Newton ; le terme de gauche est l'accélération de la particule, tandis que le terme de droite est la somme des forces qui s'exercent sur la particule. Ces forces sont des forces gravitationnelles, proportionnelles aux masses concernées et variant proportionnellement à l'inverse du carré de la distance de ces masses. Puisqu'il faut tenir compte de la direction de ces forces, il faut insérer un q_j − q_k au numérateur et le compenser par un cube au dénominateur (et non plus un simple carré).

Problème à deux corps ou mouvement keplerien

Premier triomphe de la mécanique de Newton, le problème à deux corps est entièrement soluble analytiquement : on dit qu'il s'agit d'un problème intégrable. Tous les étudiants de premier cycle en physique en découvrent un jour les rouages^[1].

Problème à N corps

En dehors de quelques cas rarissimes où une solution exacte est connue, il faut en général recourir à des méthodes de résolutions approchées. Deux approches sont utilisées :

• la théorie des perturbations, qui permet de faire des calculs analytiques approchés sous la forme de développements en série.

• l'analyse numérique. En programmation, le problème de la simulation de N corps devrait être théoriquement d'ordre N², car toutes les interactions de corps deux à deux devraient être considérées a priori. Des considérations de découpage spatial récursif (Voir: Algorithme de Barnes-Hut) permettent cependant d'arriver à de très correctes approximations en un temps de l'ordre de NlogN seulement.

Remarque sur le problème à trois corps

Contrairement à une idée répandue, le problème à trois corps possède une solution analytique exacte, découverte par Karl Sundman en 1909^[2]. Malheureusement, cette solution se présente sous la forme d'une série infinie qui converge très lentement, ce qui la rend inutile en pratique pour faire des prédictions en un temps raisonnable.

Le problème à trois corps a trouvé un renouveau par la solution périodique en huit , trouvée par Alain Chenciner et Richard Mongomery ( http://www.scholarpedia.org/article/Three_body_problem).

Annexes

Articles connexes

• Mécanique céleste
• Problème à deux corps
• Théorie des perturbations
• Théorie du chaos

Bibliographie

Initiation

Accessibles à partir du premier cycle universitaire.

• Florin Diacu & Philip Holmes ; Celestial Encounters - The Origin of Chaos, Princeton University Press (1996), ISBN : 0-691-00545-1. L'origine du « chaos » moderne se trouve dans les travaux pionniers d'Henri Poincaré réalisés à la fin du XIXe siècle à propos d'un vieux problème de mécanique Newtonienne : le problème à N corps. Les auteurs du présent ouvrage, mathématiciens spécialistes du domaine, retracent élégamment l'histoire de ce problème et de ses développements de Poincaré à nos jours.
• Forest R. Moulton ; An introduction to celestial mechanics, Dover (1970) ISBN : 0-48664-687-4. Réédition de la seconde édition publiée originellement en 1914 ; un ouvrage d'introduction très clair.
• Bill Casselman ; The three body problem, Société Américaine de Mathématiques. Quelques solutions exactes du problème à trois corps, des plus anciennes (Euler, Lagrange, Hill) à la plus récente : la chorégraphie en forme de 8 d'Alain Chenciner et al. (2000).
• Sverre J. Aarseth ; www.sverre.com. Le site personnel d'un professeur d'astronomie à l'université de Cambridge spécialiste de l'intégration numérique des équations différentielles du problème à N corps. On peut d'ailleurs télécharger ses codes de calcul sur le serveur ftp de l'université de Cambridge, ou encore à partir de cette page web.

Textes plus techniques

Les modernes

• Malte Henkel  ; Sur la solution de Sundman du probleme des trois corps, Philosophia Scientiae 5 (2) (2001), 161-184. Texte complet disponible sur l'ArXiv : physics/0203001.
• Douglas C. Heggie ; The Classical Gravitational N-Body Problem, Encyclopaedia of Mathematical Physics, Elsevier (A paraître : 2006). Texte complet disponible sur l'ArXiv : astro-ph/0503600.
• Vladimir I. Arnold, V.V. Kozlov & A.I. Neishtadt ; Mathematical Aspects of Classical and Celestial Mechanics, Encyclopaedia of Mathematical Sciences, Springer-Verlag (2^e édition-1993).
• Vladimir I. Arnold ; Mathematical Methods of Classical Mechanics, Springer-Verlag (2^e édition-1989) ISBN : 0-387-96890-3. Une synthèse de l'état de l'art en mécanique analytique (formalismes Lagrangien & Hamiltonien) avec l'accent mis sur l'interprétation géométrique de ces formalismes, par l'un des plus brillants mathématiciens du domaine. À partir du second cycle universitaire.
• Christian Marchal : the three-body problem , Elsevier , 1990;ISBN 0-444-41813-X : livre avec beaucoup de détails très précieux pour un élève de dynamique des systèmes gravitationnels. Evidemment , il ne peut intégrer les travaux Chenciner , Simo , Saari.
• Carl L. Siegel & Jürgen Moser ; Lectures on celestial mechanics, Classics in Mathematics, Springer-Verlag (1995). Quelques résultats mathématiques sur le problème à trois corps. Niveau second cycle universitaire minimum.
• June Barrow-Green ; Poincaré & the three-body problem, History of Mathematics (Vol. 11), American Mathematical Society & London Mathematical Society (1997).
• Donald G. Saari ; Collisions, Rings, and Other Newtonian N-Body Problems, CBMS Regional Conference Series in Mathematics 104, American Mathematical Society (2005), ISBN 0-8218-3250-6.
• Kenneth R. Meyer, Glen R. Hall ; Introduction to Hamiltonian Dynamical Systems and the N-Body Problem, Applied Mathematical Sciences 90, Springer-Verlag (1991), ISBN 038797637X.
• Vladimir I. Arnold & André Avez ; Ergodic Problems of Classical Mechanics, Advanced Book Classics, Pearson Addison Wesley (Mai 1989) ASIN : 0201094061. Il existe aussi en français! Problèmes ergodiques de la mécanique classique ; ed Gauthier-villars , 1967.

Les classiques

• Pierre-Simon Laplace ; Traité de mécanique céleste, Editions Jacques Gabay (1990). Réédition d'un ouvrage classique de la fin du XIXe siècle, en 4 volumes. Niveau second cycle universitaire.
• François-Félix Tisserand ; Traité de mécanique céleste, Editions Jacques Gabay (1990). Réédition d'un ouvrage classique de la fin du XIXe siècle, en 4 volumes. Niveau second cycle universitaire.
• Henri Poincaré ; Leçons de mécanique céleste, 3 tomes, (1905-1910), réédité par Jacques Gabay, Paris (2003). Une somme de référence, par le grand mathématicien qui a tant contribué au sujet. Niveau second cycle universitaire.

Analyse numérique

• Sverre J. Aarseth ; Gravitational N-body Simulations: Tools and Algorithms, Cambridge Monographs on Mathematical Physics, Cambridge University Press (2003), ISBN 0521432723.
• Piet Hut and Jun Makino ; The Art of Computational Science [1]
• A. Marciniak ; Numerical Solutions of the N-Body Problem, Mathematics and its Applications, Springer-Verlag (1989), ISBN 9027720584.

Quelques travaux récents

• Alain Chenciner & Richard Montgomery ; A remarkable periodic solution of the three-body problem in the case of equal masses, Annals of Mathematics (2) 152 (2000), no. 3, 881--901. Texte complet disponible sur l'ArXiv : math.DS/0011268.
• Cristopher Moore & Michael Nauenberg ; New Periodic Orbits for the n-Body Problem, (2005). Texte complet disponible sur l'ArXiv : math.DS/0511219.
• C. Duval, G. Gibbons & P. Horvathy  ; Celestial Mechanics, Conformal Structures, and Gravitational Waves, Physical Review D 43 (1991), 3907. Texte complet disponible sur l'ArXiv : hep-th/0512188.

Références

• Portail des mathématiques
• Portail de l’astronomie
• Portail de la physique