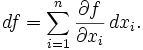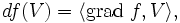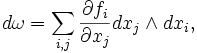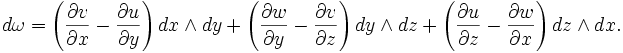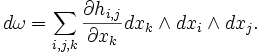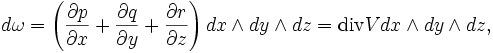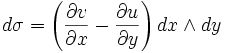- Derivee exterieure
-
Dérivée extérieure
En mathématiques, la dérivée extérieure, opérateur de la topologie différentielle, étend le concept de la différentielle d'une fonction aux formes différentielles de plus haut degré.
Elle permet de définir les formes différentielles fermées et exactes. Elle est importante dans la théorie d'intégration des variétés, et elle est la différentielle employée pour définir la cohomologie de De Rham et de Alexander-Spanier. Sa forme actuelle fut inventée par Élie Cartan.
Sommaire
Définition
Pour toute variété différentielle M, A(M) désigne (ici) l'espace gradué des formes différentielles sur M. Il existe un unique opérateur linéaire
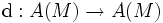 vérifiant :
vérifiant :- d est un opérateur linéaire gradué de degré 1 et induit en particulier des applications linéaires
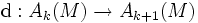 ;
; - Pour toutes formes différentielles α et β de degrés respectifs k et q, on a :
![\mathrm d\left[\alpha\wedge \beta\right]=\mathrm d\alpha\wedge \beta+(-1)^k \alpha \wedge \mathrm d\beta](/pictures/frwiki/101/e533eff4cd3cf059fed42603175caa6a.png) ;
; - Le carré de d est nul : d2 = 0 ;
- Pour toute fonction
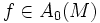 , df est la différentielle de f.
, df est la différentielle de f.
Expression en coordonnées locales
La dérivée extérieure d'une forme différentielle de degré k est une forme différentielle de degré k + 1.
Pour ω = fI dxI de forme k sur Rn, la définition est la suivante:
Pour les formes k générales: ΣI fI dxI (où le multi-indice I dépasse tous les sous-ensembles ordonnés de {1, ..., n} de cardinalité k), nous ne faisons qu'étendre linéairement. Notez que si i = I ci-dessus alors
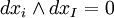 (voir produit extérieur).
(voir produit extérieur).Propriétés
La différentiation extérieure satisfait trois propriétés importantes:
- la linéarité
- la règle du produit extérieur (voir antidérivation)
- et d2 = 0, une formule codifiant l'égalité des dérivées partielles mixtes, tel que
en tout temps.
Il peut être montré que cette dérivée extérieure est uniquement déterminée par ces propriétés et son accord avec la différentielle sur les formes 0 (fonctions).
Le noyau de d contient les formes closes, et l'image des formes exactes (cf. différentielle exacte).
Formule invariante
Étant donné ω de forme k et des champs vectoriels arbitraires lisses V0,V1, …, Vk nous avons
où
![[V_i,V_j]\,\!](/pictures/frwiki/50/2db3afadb73ddd689dd18cb0a65c5897.png) dénote le crochet de Lie et
dénote le crochet de Lie et 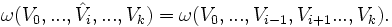
En particulier, pour les formes 1 nous avons:
- dω(X,Y) = X(ω(Y)) − Y(ω(X)) − ω([X,Y]).
Lien avec le calcul vectoriel
La correspondance suivante révèle environ une douzaine de formules du calcul vectoriel en tant que seulement des cas spéciaux des trois règles de différentiation extérieure ci-dessus.
Gradient
Pour une forme 0, qui est une fonction lisse f: Rn→R, nous avons
Alors
où grad f dénote le gradient de f et
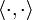 est le produit scalaire.
est le produit scalaire.Rotationnel
Pour
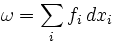 de forme 1 sur R3,
de forme 1 sur R3,qui restreinte aux trois dimensions
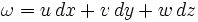 est
estAlors, pour le champ vectoriel V=[u,v,w] nous avons
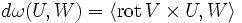 où rot V dénote le rotationnel de V, × est le produit vectoriel, et <•, •> est le produit scalaire.
où rot V dénote le rotationnel de V, × est le produit vectoriel, et <•, •> est le produit scalaire.Divergence
Pour
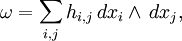 de forme 2
de forme 2Pour trois dimensions, avec
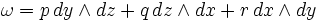 on obtient
on obtientoù V est un champ vectoriel defini par V = [p,q,r].
Exemples
Pour
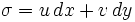 de forme 1 sur R2 nous avons
de forme 1 sur R2 nous avonsce qui est exactement la forme 2 en train de se faire intégrer dans le théorème de Green.
Voir aussi
- Dérivée covariante extérieure
- Théorème de Green
- Théorème de Stokes
- Portail des mathématiques
Catégorie : Forme différentielle - d est un opérateur linéaire gradué de degré 1 et induit en particulier des applications linéaires
Wikimedia Foundation. 2010.

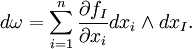
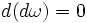
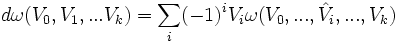
![+\sum_{i<j}(-1)^{i+j}\omega([V_i,V_j],V_0,...,\hat V_i,...,\hat V_j,...,V_k)](/pictures/frwiki/101/e750cbb8aed8b19f3c3b86d5c0f1fab8.png)