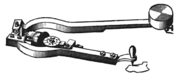
Planimetre

Planimètre de Amsler

Le planimètre est un outil qui permet la mesure mécanique directe des surfaces sur les plans, carte géographiques, etc., en en suivant le contour par l'extrémité d'un bras articulé.

Planimètre polaire de Amsler

Inventé en 1854 par le Suisse Jakob Amsler-Laffon (1823-1912), il est simple, précis et bon marché. (brevet français 24338 pour 15 ans du 27 octobre 1855^[1])

Description et Fonctionnement

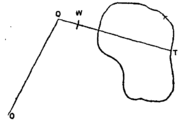Principe du planimètre polaire : le bras polaire 'OQ' tourne librement autour du point fixe 'O'. On suit le périmètre de la figure avec le curseur 'T' qui se trouve à l'extrémité du bras 'QT', fixé à 'OQ' par une simple articulation en 'Q'. La roue 'W' intègre les déplacements perpendiculaires au bras 'QT'.

Le planimètre de Amsler se compose de deux bras articulés, le bras polaire, et le bras extérieur. Une extrémité du bras polaire peut tourner autour d'un point fixe (généralement immobilisé par une masse). Le bras extérieur est fixé à l'autre extrémité du bras polaire, autour de laquelle elle est libre de tourner. À l'extrémité du bras extérieur se trouve le curseur avec l'opérateur suit le périmètre de la figure dont il veut mesurer la surface. Le bras extérieur porte de plus une roue, qui permet de mesurer les déplacements perpendiculaires au bras.

Lorsque la roue glisse en se déplaçant, elle subit toujours une force de frottement dans la direction du glissement. Comme la roue peut tourner sur son axe, la seule force de frottement qu'elle peut transmettre au bras extérieur est parallèle à cet axe, puisqu'une force perpendiculaire la ferait immédiatement tourner: la roue tourne toujours de manière à ce que la force de frottement transmise soit en permanence parallèle à son axe. La roue décompose donc en permanence les déplacements de son point de contact en un déplacement parallèle à l'axe (qui entraîne un frottement) et un déplacement perpendiculaire (qui la fait tourner).

Lorsque le curseur est déplacé dans une direction perpendiculaire au bras extérieur, la roue tourne, et sa rotation est proportionnelle au déplacement du curseur. Lorsqu'il est déplacé dans la direction du bras extérieur, en revanche, la roue glisse sans tourner, et n'enregistre pas de déplacement. Globalement, la rotation de la roue intègre la projection du déplacement du curseur sur la direction perpendiculaire au bras extérieur.

Or, lorsque le curseur décrit une courbe fermée, cette intégrale est proportionnelle à la surface délimitée par la courbe.

Démonstration

Planimètre Keuffel & Esser Co., 1908

Le Théorème de Green relie l'intégrale curviligne d'un champ le long d'une courbe fermée avec l'intégrale du rotationnel de ce champ sur la surface correspondante:

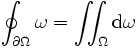
Ici, le dispositif intègre donc un champ de vecteurs F qui associe en chaque point M du plan atteint par le curseur un vecteur unitaire perpendiculaire au bras S, dans la position qu'il prend en ce point.

On démontre (tout calcul fait) que le rotationnel de ce champ est constant. L'intégrale sur la surface est donc simplement proportionnel à cette surface.

Planimètre de Prytz

Planimètre de Prytz
('Q' est massif)

Ce planimètre consiste en une simple tige, dont une extrémité porte le curseur, et l'autre est taillée en une lame parallèle à la tige pour éviter tout glissement perpendiculaire à la tige (une roulette remplirait le même rôle). Le fil de la lame est généralement un peu courbe, ce qui donne à l'instrument l'allure générale d'une hachette, d'où il tire son surnom.

Quand le curseur décrit la frontière de la surface à mesurer, l'autre extrémité suit une tractrice. Lorsque le curseur a parcouru la courbe, l'angle dont a varié la tige est à peu près proportionnel à la surface.

La valeur mesurée de la surface est: déplacement du point de contact (déplacement curviligne, le long de l'arc dont le rayon formé par le bras) fois longueur du bras, c'est à dire la surface balayée par le bras pour le remettre dans sa position initiale.

C'est un instrument peu précis, dont la précision augmente avec la longueur.

Une première source d'imprécision est que le déplacement du bras est souvent mesuré en distance rectiligne, alors que pour une meilleure précision il devrait l'être suivant sa trajectoire curviligne de retour. Pour compenser cette imprécision, le bras de certains planimètres est courbe, et porte une graduation le long de laquelle la mesure du déplacement peut être faite.

Mais la principale source d'imprécision est que la surface mesurée est très exactement celle délimitée par les deux positions extrêmes du bras, et par la trajectoire de l'extrémité tractée (et non l'arc de cercle, ce n'est donc pas exactement celle balayée par le bras au retour). Il n'est pas facile de compenser exactement cette erreur systématique; tout au plus peut-on l'atténuer en s'arrangeant pour que les écarts de la trajectoire de l'extrémité tractée soient répartis de manière à peu près équilibrée de part et d'autre de l'arc de cercle, donc en choisissant un point de départ à la même distance de l'extrémité tratée que le centre de gravité de la surface (qu'il faut estimer à vue).

Liens externes

• Marie-José Durand-Richard, Loïc Petitgirard, Les instruments du calcul savant : Planimètre polaire d'Amsler et intégraphe, CNRS
• (en) Paul Kunkel, The Planimeter But what about a polar planimeter?, 4 septembre 2003, une jolie démonstration.
• (en) Un site sur les planimètres
• (en) fonctionnement d'un planimètre de Prytz

Références

• Portail des technologies