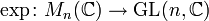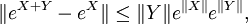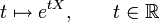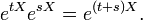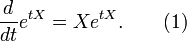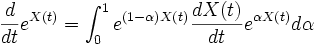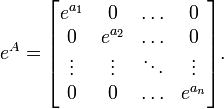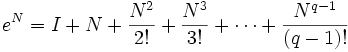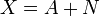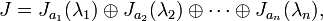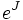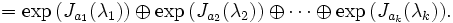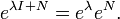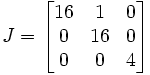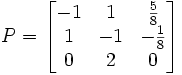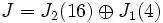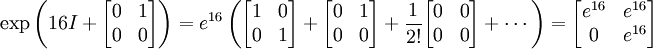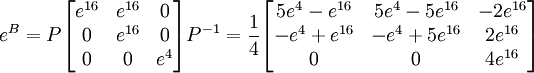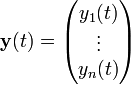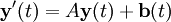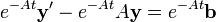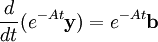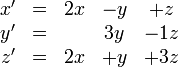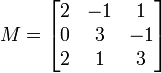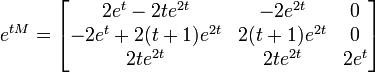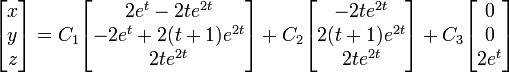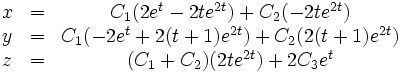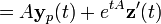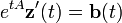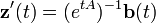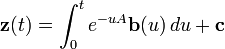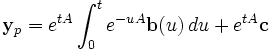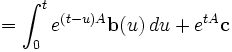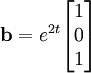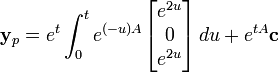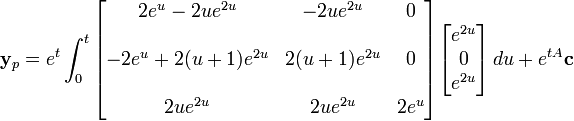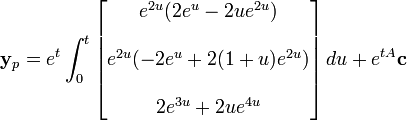- Exponentielle de matrice
-
Exponentielle d'une matrice
En mathématiques, l'exponentielle d'une matrice est une fonction d'une matrice carrée semblable à l'exponentielle. De façon abstraite, elle fait le pont entre l'algèbre de Lie sur une matrice et le groupe de Lie qui lui correspond.
Sommaire
Définition
Définition-théorème — La série d'application de terme général
converge normalement sur toute partie bornée de
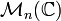 . On appelle alors exponentielle l'application de
. On appelle alors exponentielle l'application de 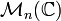 dans
dans 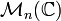 définie parDémonstration
définie parDémonstrationSoit
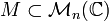 bornée. Il existe donc
bornée. Il existe donc 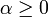 tel que
tel queOn alors pour tout
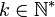 et pour tout
et pour tout 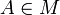 :
:Or
 est majorée par eα qui est fini, ce qui montre la convergence normale.
est majorée par eα qui est fini, ce qui montre la convergence normale.À noter que pour n=1, on retombe bien sur la définition de l'exponentielle classique.
Propriétés
Soient X et Y deux matrices n×n complexes et soient a etb deux nombres complexes. La matrice identité est dénotée I, et la matrice nulle, 0. L'exponentielle d'une matrice possède ces propriétés :
- e0 = I
- eaXebX = e(a + b)X
- eXe − X = I
- Si XY = YX, alors eXeY = eX + Y
- Si Y est une matrice inversible, alors
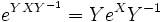 .
. - det(eX) = etr(X)
- exp(XT) = (eX)T, où XT désigne la transposée de X. Il s'ensuit que si X est une matrice symétrique, alors eX est aussi symétrique, et que si X est une matrice antisymétrique, alors eX est une matrice orthogonale.
- exp(X*) = (eX)*, où X* signifie le conjugué de la matrice transposée de X. Il suit que si X est une matrice hermitienne, alors que eX est aussi hermitienne, et que si X est une matrice antihermitienne, alors eX est une matrice unitaire.
Équations différentielles linéaires
Une des premières applications de l'exponentielle de matrices est la résolution des équations différentielles ordinaires. En effet, de l'équation (1) ci-dessous, on déduit que la solution de :
où A est une matrice, est donnée par
L'exponentielle d'une matrice peut aussi servir à résoudre les équations non-homogènes :
Voir la section Applications pour un exemple.
Il n'existe pas de solution explicite pour les équations différentielles de la forme :
où A n'est pas constant, mais la série de Magnus donne la solution en tant que somme infinie.
L'exponentielle d'une somme
On sait que l'identité ex + y = exey est valable pour tous nombres complexes x et y. On peut en fait montrer qu'elle est également valable pour deux matrices qui commutent. Autrement dit, si les matrices X et Y commutent, alors
- eX + Y = eXeY
Cependant, si ce n'est pas le cas, alors l'égalité n'est pas nécessairement vraie. Dans ce cas, la formule de Baker-Campbell-Hausdorff donne l'expression de eX + Y − eXeY en fonction du crochet [X,Y] de X et Y, et de tous les crochets itérés. Plus précisément, cette formule donne le logarithme de eXeY, par une série ne faisant intervenir que X, Y et leurs crochets. Les premiers termes sont les suivants:
L'application exponentielle
L'exponentielle d'une matrice est toujours inversible. L'inverse de eX est donné par e−X. Dès lors, cette fonction nous donne une application
de l'ensemble des matrices n×n vers le groupe général linéaire, c'est-à-dire le groupe de toutes les matrices inversibles. On appelle logarithme d'une matrice X toute matrice Y telle que eY = X ; le logarithme de X n'est pas unique en général.
Pour deux matrices X et Y, nous avons
où || · || désigne une norme matricielle arbitraire. Il suit que l'application exponentielle est continue et lipschitzienne sur tout sous-ensemble compact de Mn(C).
La bijection
définit une courbe de classe
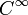 dans le groupe linéaire qui passe par l'identité en t = 0. Cette courbe est en fait un sous-groupe à un paramètre de
dans le groupe linéaire qui passe par l'identité en t = 0. Cette courbe est en fait un sous-groupe à un paramètre de  puisque
puisqueLa dérivée de cette courbe au point t est donnée par
La dérivée au point t = 0 est la matrice X, ce qui revient à dire que X génère ce sous-groupe à un paramètre.
Plus généralement,
Calculs de l'exponentielle d'une matrice
Le calcul d'une exponentielle de matrice n'est pas a priori un problème facile. Cependant, dans certains cas, et notamment ceux d'une matrice diagonale et d'une matrice nilpotente, il ne présente aucune difficulté. Une fois cette remarque faite, le cas général peut se traiter en se ramenant aux deux cas précédents.
Matrice diagonale
Si A est une matrice diagonale, c'est-à-dire :
alors son exponentielle est obtenue en calculant l'exponentielle de chacun des termes de la diagonale principale :
Cette propriété permet de calculer simplement l'exponentielle des matrices diagonalisables. Si A = UDU−1, avecD est diagonale, alors eA = UeDU−1.
Matrice nilpotente
Une matrice N est nilpotente si Nq = 0 pour un entier q. Dans ce cas, l'exponentielle d'une matrice eN se calcule directement à partir de son développement en série, puisque celui-ci ne comporte alors qu'un nombre fini de termes :
Généralisation
Lorsque le polynôme minimal d'une matrice X est scinde, X peut s'exprimer sous la forme
où
- A est diagonalisable
- N est nilpotente
- A commute avec N.
C'est la décomposition de Dunford.
Dès lors, le calcul de l'exponentielle de X se réduit aux deux cas précédents :
- eX = eA + N = eAeN
Dans le cas complexe, on peut aussi faire appel à la réduction de Jordan.
Soit J la forme de Jordan de X, et P la matrice de passage. Alors,
- eX = PeJP − 1
Puisque
En conséquence, il faut seulement connaître la méthode pour calculer l'exponentielle d'un bloc de Jordan. Chacun est de la forme
où N est la matrice nilpotente spéciale. L'exponentielle du bloc est donné par
Exemple de calculs
Soit la matrice
qui a la forme de Jordan
et la matrice de transition
Maintenant,
et
-
eB = PeJP − 1 
Alors,
L'exponentielle de la matrice 1×1 est triviale, avec eJ1(4)=e4, d'où
Applications
Équations différentielles linéaires
L'exponentielle d'une matrice peut servir à résoudre des équations différentielles linéaires.
Sachant que y′ = Cy a pour solution eCt, considérons le vecteur
Nous pouvons exprimer un système d'équations différentielles linéaires sous la forme
En multipliant par e−At, nous avons
La résolution du système se ramène donc au calcul de eAt.
Exemple (équation homogène)
Supposons que nous ayons
La matrice associée est
et son exponentielle est
La solution générale du système est donc
c'est-à-dire
Exemple (équation non-homogène, variation de la constante)
Pour une équation non-homogène, on peut utiliser une méthode semblable à la variation de la constante.
Nous cherchons une solution de la forme yp(t)=exp(tA)z(t) :
Avec yp comme solution :
Alors,
où c dépend des conditions initiales.
Exemple (non-homogène)
Supposons que nous ayons
Nous avons donc
et
Comme auparavant, la somme de la solution homogène et de la solution particulière donne la solution générale. La solution homogène étant connue, il suffit de trouver la solution particulière.
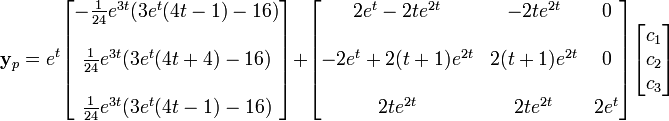 ,
,
expression qui peut être simplifiée pour obtenir la solution particulière cherchée.
Bibliographie
- Roger A. Horn et Charles R. Johnson, Topics in Matrix Analysis, Cambridge University Press, 1991. ISBN 0-521-46713-6.
- Portail des mathématiques
Catégorie : Matrice
Wikimedia Foundation. 2010.

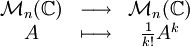
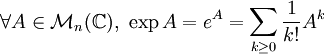
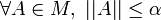
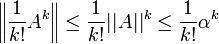
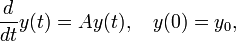
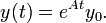
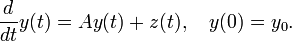
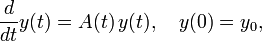
![\begin{align}\log(\exp(X)\exp(Y))&=X+Y+\frac{1}{2}[X,Y]+
\frac{1}{12}([X,[X,Y]]+[Y,[Y,X]])+\frac{1}{24}[X,[Y,[X,Y]]]\\
&\quad
- \frac{1}{720}([[[[X,Y],Y],Y],Y] +[[[[Y,X],X],X],X])
\\
&\quad +\frac{1}{360}([[[[X,Y],Y],Y],X]+[[[[Y,X],X],X],Y])\\
&\quad
+ \frac{1}{120}([[[[Y,X],Y],X],Y] +[[[[X,Y],X],Y],X]) +\dots\end{align}](/pictures/frwiki/51/3bd22e4088932fceb53a608784a5cc32.png)