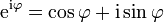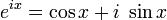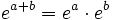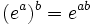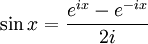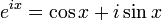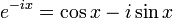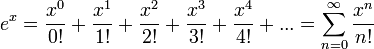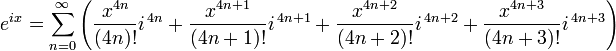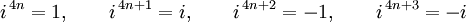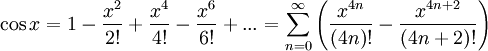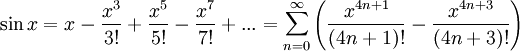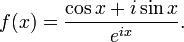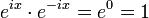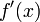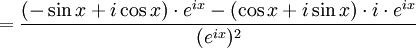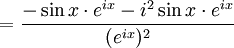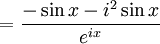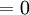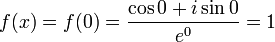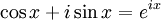Formules d'Euler

Formule d'Euler

Formule d'Euler $\mathrm e^{\mathrm i\varphi}=\cos\varphi+\mathrm i\sin\varphi$

Article d'une série sur
la constante mathématique e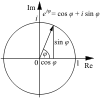



Logarithme naturel

Applications
Intérêts composés · Identité d'Euler et Formule d'Euler · Demi-vie et Croissance exponentielle/Décroissance exponentielle

Définitions
Démonstration de l'irrationalité de e · Représentations de e · Théorème de Lindemann-Weierstrass

Personnes
John Napier · Jacques Bernoulli · Leonhard Euler

Conjecture de Schanuel

La formule d'Euler, attribuée au mathématicien suisse Leonhard Euler, s'écrit pour tout nombre réel x,

$e^{ix} = \cos x + i\;\sin x$

Ici, e est la base naturelle des logarithmes, i est le nombre imaginaire, sin et cos sont des fonctions trigonométriques.

Sommaire

1 Description
2 Démonstrations
- 2.1 Par les séries de Taylor
- 2.2 Par le calcul différentiel
3 Historique
4 Voir aussi
- 4.1 Articles connexes
5 Références

Description

Cette formule peut être interprétée en disant que la fonction 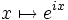$x\mapsto e^{ix}$ décrit le cercle unité dans le plan complexe lorsque x varie dans l'ensemble des nombres réels. $x$ représente la mesure de l'angle orienté que fait la demi-droite d'extrémité l'origine et passant par un point du cercle unité avec la demi-droite des réels positifs. La formule n'est valable que si sin et cos ont des arguments exprimés en radians plutôt qu'en degrés.

La démonstration est basée sur les développements de la fonction exponentielle 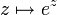$z\mapsto e^z$ de la variable complexe z et des fonctions sin et cos considérées à variables réelles. En fait, la même démonstration montre que la formule d'Euler est encore valable pour tous les nombres complexes x.

La formule d'Euler fut démontrée pour la première fois (sous une forme un peu obscure) par Roger Cotes en 1714, démontrée à nouveau et rendue populaire par Euler en 1748. Aucun de ces deux hommes ne vit l'interprétation géométrique de cette formule : le point de vue géométrique des nombres complexes considérés comme affixes de points du plan n'apparut que quelques 50 années plus tard (voir Caspar Wessel).

La formule établit un puissant lien entre l'analyse et la trigonométrie. Elle est utilisée pour représenter les nombres complexes sous forme trigonométrique et permet la définition du logarithme pour les arguments complexes. En utilisant les propriétés de l'exponentielle

$e^{a + b} = e^a \cdot e^{b}$

$(e^a)^b = e^{a b} \,$

(qui sont aussi valables pour tous les nombres complexes $a$ et $b$ ), il devient facile de dériver plusieurs identités trigonométriques ou d'en déduire la formule de Moivre. La formule d'Euler permet une interprétation des fonctions cosinus et sinus comme seules variations de la fonction exponentielle :

$\cos x = {e^{ix} + e^{-ix} \over 2}$

$\sin x = {e^{ix} - e^{-ix} \over 2i}$

Ces formules (aussi appelées formules d' Euler) peuvent servir de définition des fonctions trigonométriques de variable complexe $x$ . Pour les obtenir, vous pouvez dériver la formule d'Euler :

$e^{ix} = \cos x + i \sin x \,$

$e^{-ix} = \cos x - i \sin x \,$

et déterminer cosinus ou sinus.

Dans les équations différentielles, la fonction 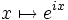$x\mapsto e^{ix}$ , est souvent utilisée pour simplifier les dérivations, même si le problème est de déterminer les solutions réelles exprimées à l'aide de sinus et cosinus. L'identité d'Euler est une conséquence immédiate de la formule d'Euler.

En électrotechnique et dans d' autres domaines, les signaux qui varient périodiquement en fonction du temps sont souvent décrits par des combinaisons linéaires des fonctions sinus et cosinus (voir analyse de Fourier), et ces dernières sont plus commodément exprimées comme parties réelles de fonctions exponentielles avec des exposants imaginaires, en utilisant la formule d'Euler.

Démonstrations

Par les séries de Taylor

Article détaillé : série de Taylor.

Le développement en série de la fonction exp de la variable réelle x peut s' écrire :

$e^x = \frac{x^0}{0!} + \frac{x^1}{1!} + \frac{x^2}{2!} + \frac{x^3}{3!} + \frac{x^4}{4!} + ... = \sum_{n=0}^\infty \frac{x^n}{n!}$

et s' étend à tout nombre complexe x .

Maintenant si nous injectons i dans l'exposant, nous obtenons :

$e^{ix} = \sum_{n=0}^\infty \frac{{(ix)}^n}{n!} = \sum_{n=0}^\infty \frac{i^n x^n}{n!} = \sum_{n=0}^\infty \frac{x^n}{n!} i^n$

Nous pouvons regrouper ses termes pour obtenir cette écriture dégénérée :

$e^{ix} = \sum_{n=0}^\infty \left( \frac{x^{4n}} {(4n)!} i^{\,4n} + \frac{x^{4n+1}}{(4n+1)!} i^{\,4n+1} + \frac{x^{4n+2}}{(4n+2)!} i^{\,4n+2} + \frac{x^{4n+3}}{(4n+3)!} i^{\,4n+3} \right)$

Pour simplifier cela, nous utilisons les propriétés de base suivantes de i :

$i^0 = 1, \qquad i^1 = i, \qquad i^2 = -1, \qquad i^3 = -i, \qquad i^4 = 1, \ldots$

en généralisant à tout exposant entier, on a pour tout n :

$i^{\,4n} = 1, \qquad i^{\,4n+1} = i, \qquad i^{\,4n+2} = -1, \qquad i^{\,4n+3} = -i$

Ainsi,

$e^{ix} = \sum_{n=0}^\infty \left( \frac{x^{4n}} {(4n)!} + \frac{x^{4n+1}}{(4n+1)!} i - \frac{x^{4n+2}}{(4n+2)!} - \frac{x^{4n+3}}{(4n+3)!} i \right)$

en réarrangeant les termes et en séparant la somme en deux (ce qui est possible puisque les deux séries sont absolument convergentes) :

$e^{ix} = \sum_{n=0}^\infty \left( \frac{x^{4n}} {(4n)!} - \frac{x^{4n+2}}{(4n+2)!} \right) + i\,\sum_{n=0}^\infty \left( \frac{x^{4n+1}}{(4n+1)!} - \frac{x^{4n+3}}{(4n+3)!} \right)$

Pour avancer un peu plus, nous utilisons les développements en série de Taylor des fonctions cosinus et sinus:

$\cos x = 1 - \frac{x^2}{2!} + \frac{x^4}{4!} - \frac{x^6}{6!} + ... = \sum_{n=0}^\infty \left( \frac{x^{4n}} {(4n)!} - \frac{x^{4n+2}}{(4n+2)!} \right)$

$\sin x = x - \frac{x^3}{3!} + \frac{x^5}{5!} - \frac{x^7}{7!} + ... = \sum_{n=0}^\infty \left( \frac{x^{4n+1}}{(4n+1)!} - \frac{x^{4n+3}}{(4n+3)!} \right)$

Ce qui, en remplaçant dans les formules précédentes de e^ix, donne :

$e^{ix} = \cos x + i\; \sin x$

comme requis.

Par le calcul différentiel

Article détaillé : calcul différentiel.

Définissons l'application 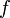$f \$ par

$f(x) = \frac{\cos x+i\sin x}{e^{ix}}. \$

Cette application est bien définie puisque

$e^{ix}\cdot e^{-ix}=e^0=1 \$

implique que 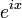$e^{ix} \$ n'est jamais nul.

L'application 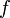$f \$ est le quotient de deux fonctions dérivables et donc est dérivable (dérivation d'un quotient) et sa dérivée est donnée par:

$f'(x)\,$	$= \displaystyle\frac{(-\sin x+i\cos x)\cdot e^{ix} - (\cos x+i\sin x)\cdot i\cdot e^{ix}}{(e^{ix})^2} \$
	$= \displaystyle\frac{-\sin x\cdot e^{ix}-i^2\sin x\cdot e^{ix}}{(e^{ix})^2} \$
	$= \displaystyle\frac{-\sin x-i^2\sin x}{e^{ix}} \$
	$= \displaystyle\frac{-\sin x-(-1)\sin x}{e^{ix}} \$
	$= \displaystyle\frac{-\sin x+\sin x}{e^{ix}} \$
	$= 0 \$

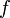Ainsi, $f \$ est une fonction constante et continue sur $\mathbb{R}$ . D'où

$f(x)=f(0)=\frac{\cos 0 + i \sin 0}{e^0}=1$

$\frac{\cos x + i \sin x}{e^{ix}}=1$

$\displaystyle\cos x + i \sin x=e^{ix}$

Historique

La formule d'Euler fut démontrée pour la première fois par Roger Cotes en 1714 sous la forme ln(cos(x) + i sin(x)) = ix (où ln désigne le logarithme népérien, c'est-à-dire Log de base e)^[1]. Ce fut Euler qui publia la formule sous sa forme actuelle en 1748, en basant sa démonstration sur l'égalité entre deux séries. Aucun des deux mathématiciens ne donna une interprétation géométrique de la formule : l'interprétation des nombres complexes comme des points d'un plan ne fut vraiment évoquée que cinquante années plus tard (voir Caspar Wessel).

Voir aussi

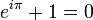
Références

↑ John Stillwell, Mathematics and Its History, Springer, 2002

Portail des mathématiques

Ce document provient de « Formule d%27Euler ».

Catégories : Nombre complexe | Analyse complexe | Trigonométrie | Pi

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Formules d'Euler de Wikipédia en français (auteurs)

Игры ⚽ Нужно решить контрольную?

Regardez d'autres dictionnaires:

formules d'Euler — ● formules d Euler Relation F + S = A + 2, vraie pour tout polyèdre convexe compact, qui lie le nombre F de ses faces, le nombre S de ses sommets et celui A de ses arêtes. Formules et où x ∊ R, obtenues à partir des relations ch ix = cos x et sh… … Encyclopédie Universelle
EULER (L.) — Avec Joseph Louis Lagrange, son émule plus jeune, Leonhard Euler est l’un des deux géants mathématiques qui ont dominé la science du XVIIIe siècle. Ses travaux, d’une abondance inégalée, couvrent tout le champ des mathématiques, de la mécanique… … Encyclopédie Universelle
Formules trigonométriques — Identité trigonométrique Une identité trigonométrique est une relation impliquant des fonctions trigonométriques et qui est vérifiée pour toutes les valeurs des variables intervenant dans la relation. Ces identités peuvent être utiles quand une… … Wikipédia en Français
Formules De Mécanique Des Fluides — Cet article fait partie de la série formulaire de physique Optique Électro Magnéstatique Physique quantique Thermodynamique Mécanique des fluides … Wikipédia en Français
Formules de mecanique des fluides — Formules de mécanique des fluides Cet article fait partie de la série formulaire de physique Optique Électro Magnéstatique Physique quantique Thermodynamique Mécanique des fluides … Wikipédia en Français
Formules pour les nombres premiers — En mathématiques, la recherche de formules exactes donnant tous les nombres premiers (ou même donnant uniquement des nombres premiers) s est généralement avérée vaine, ce qui a amené à se contenter de formules approchées. Cette page recense les… … Wikipédia en Français
Euler — Leonhard Euler « Euler » redirige ici. Pour les autres significations, voir Euler (homonymie). Leonhard Euler … Wikipédia en Français
Formules de mécanique des fluides — Sommaire 1 Statique des fluides 1.1 Loi fondamentale de la statique des fluides 1.2 Poussée d Archimède 2 Dynamique des fluides parfaits inc … Wikipédia en Français
Trigonométrie classique et formules — Identité trigonométrique Une identité trigonométrique est une relation impliquant des fonctions trigonométriques et qui est vérifiée pour toutes les valeurs des variables intervenant dans la relation. Ces identités peuvent être utiles quand une… … Wikipédia en Français
Formule d'Euler — eiφ = cos φ + isin φ La formule d Euler, attribuée au mathématicien suisse Leonhard Euler, s écrit pour tout nombre réel x … Wikipédia en Français

Dictionnaires et Encyclopédies sur 'Academic'

Formules d'Euler

Formule d'Euler

Sommaire

Description