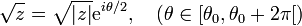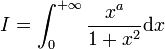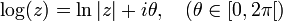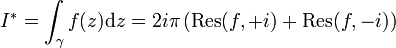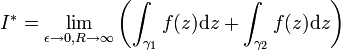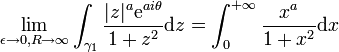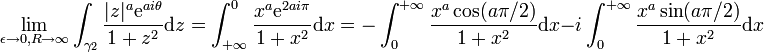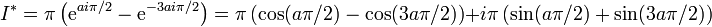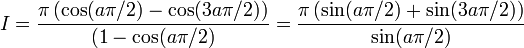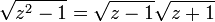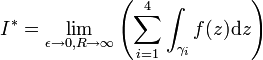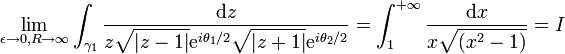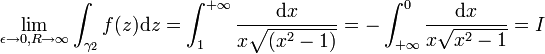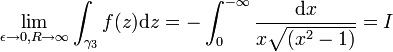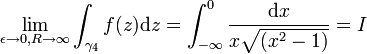Fonction multiforme

Fonction multivaluée

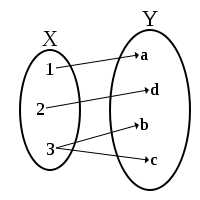
Ce diagramme ne représente pas une vraie fonction car à l'élément 3 appartenant à X correspond deux éléments dans Y : b et c.

En mathématiques, une fonction multivaluée (aussi appelée multiforme) est une fonction qui associe à une variable plusieurs valeurs. À proprement parler, ce n'est donc pas une fonction puisque par définition une fonction associe une unique valeur à un point de son domaine.

Elles proviennent souvent des fonctions qui ne sont pas injectives. Elles ne possèdent pas à proprement parler de fonctions réciproques mais on peut les considérer dans le cadre des fonctions multivaluées.

Ces relations sont particulièrement intéressantes en analyse complexe où l'on peut considérer des déterminations, c'est-à-dire des restrictions sur ces relations qui en font des fonctions et qui permettent de calculer certaines intégrales réelles par le biais du théorème des résidus comme ce sera illustré plus bas.

Sommaire

1 Exemples
- 1.1 La racine carrée
- 1.2 Le logarithme complexe
2 Déterminations
3 Application au calcul d'intégrales réelles
- 3.1 Exemple avec le logarithme complexe
- 3.2 Exemple avec la racine carrée complexe
4 Surfaces de Riemann
5 Voir aussi
6 Notes
7 Références

Exemples

La racine carrée

Article détaillé : racine carrée.

Article détaillé : racine d'un nombre complexe.

Dans les réels, à chaque élément positif x, la relation "racine carrée" fait correspondre deux éléments $| y |$ et $- | y |$ avec $| y | 2 = x$ . On se restreint de manière habituelle à la valeur positive $| y |$ pour avoir alors la fonction racine carrée.

Dans les complexes, en définissant un élément z du plan complexe 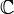$\mathbb C$ par $z = | z | e i θ$ avec $θ$ l'argument de z, les racines carrées de z sont les nombres $w k$ ( $k\in\mathbb Z$ ) donnés par :

$w_k = \sqrt{|z|}\mathrm{e}^{i\theta/2}\mathrm{e}^{i\pi k}$

on vérifie en effet que 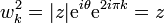$w_k^2 = |z|\mathrm{e}^{i\theta} \mathrm{e}^{2i\pi k} = z$ puisque

e 2 i π k

vaut l'unité pour tout entier k.

Le logarithme complexe

Article détaillé : logarithme complexe.

En définissant un élément z du plan complexe comme précédemment, le logarithme complexe de z sont les nombres $w k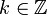$ ( $k\in \mathbb Z$ ) donnés par :

w k = ln | z | + i θ + 2 i π k

on vérifie en effet que $exp(w k) = | z | e i θ e 2 i π k = z$ puisque, comme précédemment, $e 2 i π k$ vaut l'unité pour tout entier k.

Déterminations

Pour la racine carrée complexe et le logarithme complexe, on appelle détermination une restriction sur l'argument $θ$ de la valeur correspondante. Plus explicitement, une détermination pour la racine carrée est donnée par :

$\sqrt{z} = \sqrt{|z|}\mathrm{e}^{i\theta/2}, \quad (\theta \in [\theta_0, \theta_0+2\pi[)$

avec $θ 0$ un angle quelconque caractérisant la détermination.

De même, une détermination pour le logarithme complexe est donnée par :

$\log{z} = \ln{|z|} + i\theta, \quad (\theta \in [\theta_0, \theta_0+2\pi[)$

On appelle détermination principale du logarithme la restriction de l'argument à l'intervalle semi-ouvert $[ - π,π[$ .

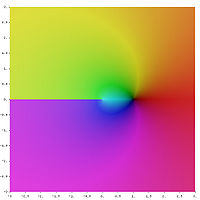
Remarquons que, à une détermination près, la fonction racine carrée complexe et le logarithme complexe sont des fonctions holomorphes sur tout le plan complexe excepté la demi-droite partant de l'origine et d'angle $θ 0$ par rapport à l'axe des abscisses. Dans le cas de la détermination principale, les deux fonctions sont holomorphes sur $\mathbb C\backslash]-\infty, 0]$ . La discontinuité sur l'axe réel négatif est illustrée sur les deux figures ci-dessous.

Détermination principale
Figure 1 : illustration de la détermination principale du logarithme complexe.	Figure 2 : illustration de la détermination principale de la racine carrée complexe.

Application au calcul d'intégrales réelles

Considérer une détermination particulière permet, en s'aidant du théorème des résidus, de calculer certaines intégrales réelles qu'il serait autrement ardu de calculer.

Remarque : la relation suivante est souvent utilisée comme ce sera illustré dans l'exemple ci-dessous : $z α = e αlog(z)$ .

Exemple avec le logarithme complexe

Figure 3 : Illustration du contour

γ

(en bleu) employé pour le premier exemple. Les deux pôles simples $\pm i$ sont représentés en rouge. La partie

γ R

représente le cercle extérieur de rayon R, la partie

γ ε

représente le demi-cercle intérieur de rayon

ε

γ 1,2

sont les deux segments restants.

Problème : calculer l'intégrale suivante :

$I = \int_0^{+\infty} {x^a\over 1+x^2}\mathrm{d}x$

pour $| a | < 1$ .

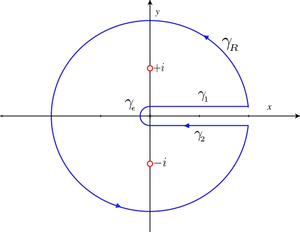
Solution : En considérant le contour $γ$ illustré à la figure 3 ainsi que la détermination suivante du logarithme :

$\mathrm{log}(z) = \ln|z| + i\theta, \quad (\theta\in[0, 2\pi[)$

(le contour "entoure" donc la discontinuité de la détermination que nous avons choisie), on obtient : pour $0 < | a | < 1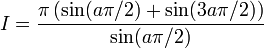$ : $I = {\pi\left(\sin(a\pi/2)+\sin(3a\pi/2)\right)\over \sin(a\pi/2)}$ et pour $a = 0$ , l'intégrale vaut $π$ .

Développement

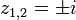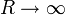La fonction f définie par $f(z) = {z^a\over 1+z^2}$ a deux pôles simples ( $z_{1,2}=\pm i$ ) tous deux d'indice +1 par rapport à $γ$ (pour $ε < 1$ et $R > 1$ ). A la limite $\epsilon\to 0$ et $R\to \infty$ , le théorème des résidus nous donne donc :

$I^* = \int_\gamma f(z) \mathrm{d}z = 2i\pi \left(\mathrm{Res}(f, +i) + \mathrm{Res}(f, -i)\right)$

En décomposant l'intégrale curviligne en ses quatre parties principales et en appliquant le lemme d'estimation pour montrer que l'intégrale le long de $γ ε$ et celle le long de $γ R$ tendent vers zéro à la limite, il nous reste :

$I^* = \lim_{\epsilon\to 0, R\to \infty} \left(\int_{\gamma_1}f(z)\mathrm{d}z+\int_{\gamma_2}f(z)\mathrm{d}z\right)$

En utilisant la détermination choisie ci-dessus, on a que :

z a = e a log(z) = e a (ln | z | + i θ) = | z | a e a i θ

à la limite $\epsilon\to 0$ , le long du chemin $γ 1$ , l'argument $θ$ tend vers zéro ; le long du chemin $γ 2$ , l'argument tend vers $2π$ , on a donc :

$\lim_{\epsilon\to 0, R\to \infty}\int_{\gamma_1} {|z|^a\mathrm{e}^{ai\theta}\over 1+z^2}\mathrm{d}z = \int_0^{+\infty}{x^a\over 1+x^2}\mathrm{d}x$

$\lim_{\epsilon\to 0, R\to \infty}\int_{\gamma_2} {|z|^a\mathrm{e}^{ai\theta}\over 1+z^2}\mathrm{d}z = \int_{+\infty}^{0}{x^a\mathrm{e}^{2a i\pi}\over 1+x^2}\mathrm{d}x = - \int_0^{+\infty}{x^a \cos(a\pi/2) \over 1+x^2}\mathrm{d}x- i\int_0^{+\infty}{x^a \sin(a\pi/2) \over 1+x^2}\mathrm{d}x$

où l'on a utilisé la formule de Moivre dans la dernière égalité. On a donc :

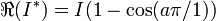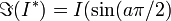
$\Re(I^*) = I(1-\cos(a\pi/1))$ ou $\Im(I^*) = I(\sin(a\pi/2)$

il nous reste à calculer $I *$ via les résidus de la fonction en $\pm i$ :

$\mathrm{Res}(f, +i) = \lim_{z\to +i} (z - i)f(z) = {i^{a}\over 2i} = {\mathrm{e}^{ai\pi/2}\over 2i}$

$\mathrm{Res}(f, -i) = {-\mathrm{e}^{3ai\pi/2}\over 2i}$

où l'on a utilisé que, dans la détermination choisie, l'argument de $+ i$ (resp. $- i$ ) est $π / 2$ (resp. $3π / 2$ ). On obtient donc :

$I^* = \pi\left({\mathrm{e}^{ai\pi/2}}-\mathrm{e}^{-3ai\pi/2}\right) = \pi\left(\cos(a\pi/2)-\cos(3a\pi/2)\right) + i\pi\left(\sin(a\pi/2)+\sin(3a\pi/2)\right)$

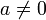et finalement pour $| a | < 1$ et $a\neq 0$ :

$I = { \pi\left(\cos(a\pi/2)-\cos(3a\pi/2)\right) \over (1-\cos(a\pi/2)} = {\pi\left(\sin(a\pi/2)+\sin(3a\pi/2)\right)\over \sin(a\pi/2)}$

où l'on a utilisé la partie réelle de $I *$ pour la première égalité et la partie imaginaire pour la seconde. Pour $a = 0$ , l'intégrale est connue et vaut $π$ , résultat que l'on retrouve par ailleurs en passant à la limite pour chacune des deux expressions possibles données ci-dessus.

Exemple avec la racine carrée complexe

Figure 4 : Illustration du contour

γ

(en bleu) employé pour le second exemple. Les deux points de branchement $\pm 1$ sont représentés en rouge. Le pôle simple restant (l'origine) est représenté en vert.

γ R

représente le cercle extérieur de rayon R,

γ ε

et son homologue représentent les demi-cercles intérieurs de rayon

ε

, les

γ i

sont les segments restants.

Problème : calculer l'intégrale suivante par le biais des résidus :

$I = \int_{1}^{+\infty} {\mathrm{d}x\over x\sqrt{x^2-1}}$

(la fonction est uniformisée par la coupure le long de l'axe réel reliant $-\infty$ à -1 et 1 à $+\infty$ .)

Solution : l'intégrande a une primitive (à savoir $-\mathrm{atan}\left[\left(x^2-1\right)^{-1/2}\right]$ ) et on a donc immédiatement 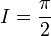$I = {\pi\over 2}$ . On obtient ce même résultat en considérant le contour $γ$ illustré à la figure 4 ci-contre et en utilisant :

$\sqrt{z^2-1} = \sqrt{z-1}\sqrt{z+1}$

Pour le premier terme du produit, on considérera la détermination suivante :

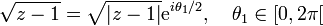$\sqrt{z-1} = \sqrt{|z-1|}\mathrm{e}^{i\theta_1/2},\quad \theta_1 \in [0, 2\pi[$ ,

pour l'autre, on considérera la détermination principale :

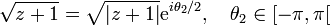$\sqrt{z+1} = \sqrt{|z+1|}\mathrm{e}^{i\theta_2/2},\quad \theta_2\in [-\pi, \pi[$ .

sous ces déterminations, la fonction est holomorphe sur $\mathbb C\backslash \left(]-\infty, -1]\cup[+1, \infty[\right)$ .

Développement

La fonction f définie par 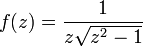$f(z) = {1\over z\sqrt{z^2-1}}$ a trois singularités^[1] : les deux points de branchement ( $\pm 1$ ) et le pôle simple (l'origine) qui est la seule singularité d'indice non nul par rapport au contour ; à la limite $\epsilon\to 0$ et $R\to \infty$ , le théorème des résidus nous donne donc :

I ^* =	∫	f(z)dz = 2iπRes(f,0)
	γ

et 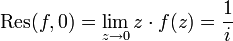$\mathrm{Res}(f, 0) = \lim_{z\to 0} z\cdot f(z) = {1\over i}$ , on a donc $I * = 2π$ .

En décomposant l'intégrale curviligne en ses sept parties principales et en appliquant le lemme d'estimation pour montrer que l'intégrale le long de $γ ε$ , $γ ε'$ et $γ R$ tendent vers zéro à la limite, il nous reste :

$I^* = \lim_{\epsilon\to 0, R\to\infty} \left(\sum_{i=1}^4 \int_{\gamma_i}f(z)\mathrm{d}z\right)$

à la limite $\epsilon\to 0$ , le long du chemin $γ 1$ , l'argument $θ$ tend vers zéro pour les deux déterminations, le long du chemin $γ 2$ , l'argument tend vers $2π$ (resp. zéro) pour la première détermination (resp. la détermination principale), le long du chemin $γ 3$ l'argument tend vers $π$ pour les deux déterminations et pour $γ 4$ , l'argument tend vers $π$ (resp. $- π$ ) pour la première détermination (resp. la détermination principale).

On a donc en notant symboliquement $θ 1$ (resp. $θ 2$ ) l'argument dans la première détermination (resp. la détermination principale) :

$\lim_{\epsilon\to 0,R\to\infty}\int_{\gamma_1} {\mathrm{d}z\over z\sqrt{|z-1|}\mathrm{e}^{i\theta_1/2}\sqrt{|z+1|}\mathrm{e}^{i\theta_2/2}}= \int_1^{+\infty}{\mathrm{d}x\over x\sqrt{(x^2-1)}} = I$

avec $θ 1 = θ 2 = 0$ pour la partie $γ 1$ . On a de même :

$\lim_{\epsilon\to 0,R\to\infty}\int_{\gamma_2} f(z)\mathrm{d}z = \int_1^{+\infty} {\mathrm{d}x\over x\sqrt{(x^2-1)}} = -\int_{+\infty}^0 {\mathrm{d}x\over x\sqrt{x^2-1}} = I$

avec $θ 1 = 2π$ , $θ 2 = 0$ et $e i π = - 1$ . Finalement on a aussi :

$\lim_{\epsilon\to 0,R\to\infty}\int_{\gamma_3} f(z)\mathrm{d}z = -\int_0^{-\infty}{\mathrm{d}x\over x\sqrt{(x^2-1)}} = I$

$\lim_{\epsilon\to 0,R\to\infty}\int_{\gamma_4} f(z)\mathrm{d}z = \int_{-\infty}^{0}{\mathrm{d}x\over x\sqrt{(x^2-1)}} = I$

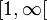où on a utilisé dans dans les deux égalités précédentes que la fonction est paire et que l'intégrale sur $]-\infty, 1]$ est égale à l'intégrale sur $[1, \infty[$ .

On a donc : $4 I = I *$ et finalement, 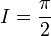$I = {\pi\over 2}$ ainsi que prévu.

Surfaces de Riemann

Article détaillé : surface de Riemann.

Surface de Riemann associée à la fonction racine carrée.

La théorie peu opérante des fonctions multivaluées pour les fonctions de la variable complexe est remplacée dans les mathématiques modernes par le concept plus abstrait de surface de Riemann.

Ce point de vue consiste à considérer le domaine de définition d'une fonction multivaluée comme d'un objet plus complexe (une variété complexe de dimension 1).

Voir aussi

Notes

↑ on parle ici de singularité au sens large du terme (et donc pas uniquement d'une singularité isolée) c'est-à-dire que la fonction n'est pas analytique en la singularité mais que n'importe quel voisinage ouvert non vide de la singularité contient au moins un point pour lequel la fonction est analytique. [MATHEWS, HOWELL - p.232]

Références

Murray R. SPIEGEL, Variables Complexes, Schaum, (ISBN 2-7042-0020-3)
John H. MATHEWS, Russel W. HOWELL, "Complex Analysis for Mathematics and Engineering", 3^d edition, 1997, Jones and Bartlett Publishers International, (ISBN 0-7637-0270-6)

Portail des mathématiques

Ce document provient de « Fonction multivalu%C3%A9e ».

Catégories : Analyse | Analyse complexe

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Fonction multiforme de Wikipédia en français (auteurs)

Игры ⚽ Нужен реферат?

Regardez d'autres dictionnaires:

fonction multiforme — daugiareikšmė funkcija statusas T sritis fizika atitikmenys: angl. many valued function; multiple valued function; multivalent function vok. mehrdeutige Funktion, f; mehrwertige Funktion, f rus. многозначная функция, f pranc. fonction multiforme … Fizikos terminų žodynas
multiforme — [ myltifɔrm ] adj. • 1440; lat. multiformis ♦ Qui se présente sous des formes variées, des aspects, des états divers et nombreux. ⇒ protéiforme. Menace multiforme. « l eau informe et multiforme » (Baudelaire). ● multiforme adjectif Qui a ou prend … Encyclopédie Universelle
Fonction exponentielle — Pour les articles homonymes, voir Exponentielle. Courbe représentative de la fonction En mathématiques, la fon … Wikipédia en Français
Fonction exponentielle (mathématiques élémentaires) — Exponentielle Pour les articles homonymes, voir Exp. Représentation graphique de la fonction exponentielle de base e (en noir), de base 10 (en rouge) et de base 1/2 (en bleu) … Wikipédia en Français
Fonction exponentielle — Exponentielle Pour les articles homonymes, voir Exp. Représentation graphique de la fonction exponentielle de base e (en noir), de base 10 (en rouge) et de base 1/2 (en bleu) … Wikipédia en Français
Fonction multivaluée — Ce diagramme représente une multifonction : à chaque élément de X on fait correspondre une partie de Y ; ainsi à l élément 3 de X correspond la partie de Y formée des deux points b et c. En mathématiques, une fonction multivaluée (aussi … Wikipédia en Français
fonction multivalente — daugiareikšmė funkcija statusas T sritis fizika atitikmenys: angl. many valued function; multiple valued function; multivalent function vok. mehrdeutige Funktion, f; mehrwertige Funktion, f rus. многозначная функция, f pranc. fonction multiforme … Fizikos terminų žodynas
fonction non uniforme — daugiareikšmė funkcija statusas T sritis fizika atitikmenys: angl. many valued function; multiple valued function; multivalent function vok. mehrdeutige Funktion, f; mehrwertige Funktion, f rus. многозначная функция, f pranc. fonction multiforme … Fizikos terminų žodynas
Fonction W De Lambert — La fonction W de Lambert, nommée ainsi d après Johann Heinrich Lambert, aussi appelée la fonction Oméga, est la réciproque de la fonction f définie par : . Ce qui implique que pour tout nombre complexe z, nous avons : Puisque la… … Wikipédia en Français
Fonction w de lambert — La fonction W de Lambert, nommée ainsi d après Johann Heinrich Lambert, aussi appelée la fonction Oméga, est la réciproque de la fonction f définie par : . Ce qui implique que pour tout nombre complexe z, nous avons : Puisque la… … Wikipédia en Français

Dictionnaires et Encyclopédies sur 'Academic'

Fonction multiforme

Fonction multivaluée

Sommaire