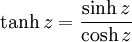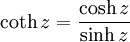Trigonometrie complexe
- Trigonometrie complexe
-
Wikimedia Foundation.
2010.
Contenu soumis à la licence CC-BY-SA. Source : Article Trigonometrie complexe de Wikipédia en français (auteurs)
Regardez d'autres dictionnaires:
Trigonométrie complexe — Extension des fonctions circulaires Dans le plan des nombres complexes, grâce aux formules d Euler, les fonctions trigonométriques peuvent se définir ainsi … Wikipédia en Français
Trigonometrie — Trigonométrie Planche sur la Trigonométrie, 1728 Cyclopaedia La trigonométrie (du grec ancien τρίγωνος / trígonos, « triangulaire », et μέτρον / métron, « mesure ») est une branche des mathématiques qui traite des relations… … Wikipédia en Français
Trigonométrie — Planche sur la Trigonométrie, 1728 Cyclopaedia. La trigonométrie (du grec τρίγωνος / trígonos, « triangulaire », et μέτρον / métron, « mesure ») est une branche des mathématiques qui traite des relations entre distances et… … Wikipédia en Français
Trigonométrie classique et formules — Identité trigonométrique Une identité trigonométrique est une relation impliquant des fonctions trigonométriques et qui est vérifiée pour toutes les valeurs des variables intervenant dans la relation. Ces identités peuvent être utiles quand une… … Wikipédia en Français
trigonométrie — [ trigɔnɔmetri ] n. f. • 1613; lat. sc. trigonometria (1595); cf. trigone et métrie 1 ♦ Sc. Branche des mathématiques dont le principal objet est l application du calcul à la détermination des éléments des triangles, au moyen des fonctions… … Encyclopédie Universelle
Arithmétique complexe — Nombre complexe Pour les articles homonymes, voir complexe. Les nombres complexes forment une extension de l ensemble des nombres réels. Ils permettent notamment de définir des solutions à toutes les équations polynomiales à coefficients réels.… … Wikipédia en Français
Nombre Complexe — Pour les articles homonymes, voir complexe. Les nombres complexes forment une extension de l ensemble des nombres réels. Ils permettent notamment de définir des solutions à toutes les équations polynomiales à coefficients réels. Les nombres… … Wikipédia en Français
Nombre complexe — Pour les articles homonymes, voir complexe. En mathématiques, les nombres complexes forment une extension de l ensemble des nombres réels. Ils permettent notamment de définir des solutions à toutes les équations polynomiales à coefficients réels … Wikipédia en Français
Notation complexe — Nombre complexe Pour les articles homonymes, voir complexe. Les nombres complexes forment une extension de l ensemble des nombres réels. Ils permettent notamment de définir des solutions à toutes les équations polynomiales à coefficients réels.… … Wikipédia en Français
Logarithme Complexe — Courbe de densité représentant la branche principale de la fonction logarithme complexe. En mathématiques, le logarithme complexe est une fonction généralisant la fonction logarithme naturel (définie sur … Wikipédia en Français
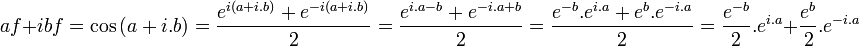
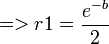 t1 = a
t1 = a 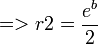 t2 = − a
t2 = − a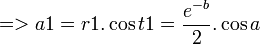
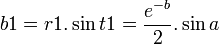
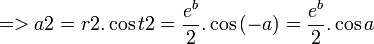
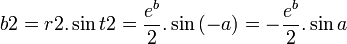
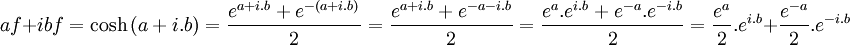
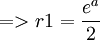 t1 = b
t1 = b 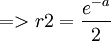 t2 = − b
t2 = − b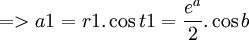
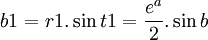
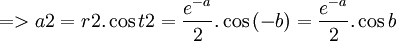
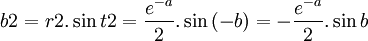

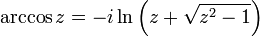
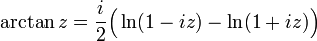
![=> af = a1 + a2 = \frac{e^{-b}}{2}.\cos{a} + \frac{e^{b}}{2}.\cos{a} = \cos{a}.[\frac{e^{-b}}{2} + \frac{e^{b}}{2}] = \cos{a}.[\frac{e^{b} + e^{-b}}{2}] = \cos{a}.\cosh{b}](/pictures/frwiki/101/e6692fabee4e452c8337c7a919828f72.png)
![=> bf = b1 + b2 = \frac{e^{-b}}{2}.\sin{a} - \frac{e^{b}}{2}.\sin{a} = \sin{a}.[\frac{e^{-b}}{2} - \frac{e^{b}}{2}] =
\sin{a}.[\frac{-1.(e^{b} - e^{-b})}{2}] = -\sin{a}.\sinh{b}](/pictures/frwiki/49/14f00a68972dbdf4d9eb1c94a87753a2.png)
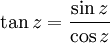
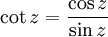
![=> af = a1 + a2 = \frac{e^{a}}{2}.\cos{b} + \frac{e^{-a}}{2}.\cos{b} = [\frac{e^{a}}{2} + \frac{e^{-a}}{2}].\cos{b} = [\frac{e^{a} + e^{-a}}{2}].\cos{b} = \cosh{a}.\cos{b}](/pictures/frwiki/97/a14dd8f5cc9ef020f5a45ed4d352e918.png)
![=> bf = b1 + b2 = \frac{e^{a}}{2}.\sin{b} - \frac{e^{-a}}{2}.\sin{b} = [\frac{e^{a}}{2} - \frac{e^{-a}}{2}].\sin{b} = [\frac{e^{a} - e^{-a}}{2}].\sin{b} = \sinh{a}.\sin{b}](/pictures/frwiki/50/23fe2de642f99c3e4753a284105475f4.png)