Figure De La Terre À La Renaissance

Le XV^e siècle est celui du renouveau en Europe. La chute de Byzance, en 1453, marque traditionnellement la fin du Moyen Âge et le début de la Renaissance. À cette époque, Nicolas de Cues (1401–1464), évêque de Brixen (Tyrol), émet des idées originales qui plongent leurs racines dans la métaphysique. Il enseigne en particulier la doctrine de l'impetus impressus, qui inspirera les travaux de Leonardo da Vinci et de Copernicus. D'autre part, Georg von Purbach (1423–1461) et son disciple Johannes Müller von Königsberg, dit Regiomontanus (1436–1476), remettent les études astronomiques à l'honneur en Europe occidentale. Johann Gutenberg (1398?–1468) invente la typographie en 1440, et l'imprimerie se développe à grande allure à partir de 1450, permettant ainsi de diffuser sur une grande base des œuvres religieuses et scientifiques. L'invention de l'imprimerie constitue un fait essentiel, capital, dont il est sans doute impossible d'exagérer l'importance. Il explique en grande partie l'essor scientifique en Europe à partir du milieu du XV^e siècle.

Copernic et le système héliocentrique

Nicolas Copernic (1472–1543), le savant humaniste qui a changé notre vision du monde en plaçant le Soleil au centre de l'Univers (peinture de Jan Matejko)

En 1543 paraît le célèbre ouvrage intitulé «Nicolai Copernici Torinensis De Revolutionibus Orbium Coelestium Libri VI» dédicacé au pape Paul III, grand protecteur des arts et des sciences, celui-là même qui engagea Michel-Ange pour décorer la chapelle Sixtine. Cet ouvrage de Nicolas Copernic (1472–1543) bouleverse les dogmes de la science officielle, en exposant le système héliocentrique. Ce dernier, pourtant présenté prudemment dans une préface rédigée par Copernic lui-même ou, plus vraisemblablement, à son insu par l'éditeur Osiander, comme une hypothèse de travail mathématique pour simplifier les calculs, et non pas comme une réalité physique, va soulever des polémiques scientifico-religieuses pendant le siècle qui va suivre. Il va finalement triompher dans le monde scientifique, mais non sans avoir fait des victimes très célèbres comme Galilée, qui eurent l'imprudence de le défendre trop vigoureusement contre les dogmes ecclésiastiques. En fait, l'idée de Copernic n'était guère nouvelle, puisqu'elle fut déjà défendue par Aristarque de Samos dix-sept siècles plus tôt. En outre, elle était «dans l'air du temps», pour ainsi dire. Pour s'en convaincre, il suffit de citer la phrase suivante de Leonardo da Vinci (1451-1519), écrite bien avant la parution de l'œuvre de Copernic : «… comment la Terre n'est pas au milieu du cercle du Soleil, ni au milieu du Monde, mais bien au milieu de ses éléments, qui l'accompagnent et lui sont unis ».

L'hypothèse héliocentrique de Copernic n'est en fait pas entièrement révolutionnaire. En effet, elle ne rompt pas avec la tradition philosophique remontant à Platon, qui veut que les astres, êtres d'essence divine, circulent sur des orbes circulaires, le cercle et la sphère étant les figures géométriques «parfaites». C'est à Kepler qu'on doit l'idée que les trajectoires des planètes ne sont pas des cercles, mais des ellipses, et c'est donc lui le grand révolutionnaire. La contribution essentielle de Copernic à la Science n'est même pas de rendre l'hypothèse héliocentrique particulièrement plausible et attrayante, mais bien de mettre le modèle héliocentrique sous une forme mathématique qui permet de comparer ses conséquences chiffrées avec celles du modèle de Ptolémée. En effet, si le modèle géocentrique de Ptolémée, avec ses très nombreux épicycles, déférents et excentriques, est particulièrement complexe, le modèle héliocentrique de Copernic reste toujours très compliqué, car il ne renonce pas à des orbites circulaires et se trouve ainsi obligé lui-aussi d'introduire un nombre élevé d'épicycles pour être en accord avec les observations cinématiques de l'époque.

Lorsque paraît l'œuvre de Copernic, la Science est surtout cultivée dans l'Italie de la Renaissance. Des mathématiciens attachés à l'université de Bologne, à savoir Gerolamo Cardano (Jérôme Cardan, 1501-1576), Niccolò Fontana Tartaglia (1499-1557), Lodovico Ferrari (1522-1565) et Raphaël Bombelli (1526-1573), donnent les formules permettant de résoudre les équations des troisième et quatrième degrés et introduisent les nombres complexes en algèbre vers 1550. Porta invente la chambre noire, qu'il perfectionne ensuite à l'aide d'une lentille servant d'objectif. Par ailleurs, on pense que c'est lui le premier inventeur de la lunette, qui révolutionnera un peu plus tard l'astronomie et la géodésie. C'est encore à cette époque que le Hollandais Gerhard Kremer, dit Mercator, propose la projection cartographique qui porte son nom. En France, le mathématicien, juriste, astronome et cryptographe François Viète (1540-1603) reprend dans son œuvre mathématique un exposé systématique de la trigonométrie plane et sphérique, dont il fournit les formules essentielles. On le considère aussi comme le père de l'algèbre classique.

Tycho Brahe, Johannes Kepler et Galilée

Tycho Brahe (1546–1601), dont les observations astronomiques très précises pour l'époque ont permis à son assistant Kepler de découvrir les lois des mouvements planétaires

En Europe du Nord œuvre, quelques décennies après la mort de Copernic, le célèbre astronome danois Tycho Brahe (1546–1601). On lui doit des méthodes d'observation et des observations astronomiques qui furent de très loin les meilleures de l'époque. La précision de ces observations, qui se situe autour de la minute de degré, ne peut guère être améliorée sans utiliser des instruments optiques. Tycho Brahe rejette le système héliocentrique de Copernic, mais se déclare en faveur d'un système du monde comparable à celui de Héraclite du Pont qui n'est ni entièrement héliocentrique ni entièrement géocentrique. Parmi ses travaux, notons aussi la publication de tables de réfraction, l'observation de la supernova de 1572, l'emploi de la méthode de triangulation en 1578 pour lever la carte de l'île de Hven où il avait fait construire selon ses propres plans son observatoire d'Uraniborg. Cette triangulation lui permet de relier l'île de Hveen à la côte voisine du Danemark. Tycho Brahe fait en outre remarquer que si les étoiles de la sphère des fixes étaient proches, leurs coordonnées devraient subir une variation parallactique annuelle, ce qui n'est pas le cas pour ses observations.

En 1582 eut lieu la réforme grégorienne du calendrier, qui ne fut toutefois pas acceptée par tous les États immédiatement, loin s'en faut. A en croire son élève Viviani, c'est l'année suivante, en 1583, que le jeune Galilée aurait remarqué l'isochronisme des petites oscillations du pendule. Vers 1595, John Napier dit Neper, baron de Merchiston (1550–1617), invente les logarithmes dont son ami Henry Briggs (1561–1630) publiera des tables à quatorze décimales vers 1624. Celles-ci furent complétées en 1628 par Adriaan Vlacq (1600–1667). Les logarithmes «naturels», ou «népériens», dont la base est le nombre e = exp(1), ne seront introduits par Leonhard Euler que vers 1748, alors que Briggs préconise dès 1617 les logarithmes décimaux, ou «communs». Le système de Napier ne correspond en fait ni à l'un ni à l'autre. Les logarithmes seront appliqués aux lignes trigonométriques, et seront adoptés avec enthousiasme par Johannes Kepler.

Galileo Galilei (1564–1642) fit des découvertes astronomiques sensationnelles avec la lunette construite par lui-même. Il fut aussi le fondateur de la physique expérimentale et découvrit notamment la loi régissant les oscillations de faible amplitude d'un pendule et la loi de la chute des corps. (Peinture de Domenico Robusti datée entre 1605 et 1607)

Galileo Galilei (Galilée), né à Pise en 1564 et mort à Arcetri près de Florence en 1642, étudie dès 1602 la chute des corps au moyen d'un plan incliné. On a vu que les lunettes d'approche semblent avoir été inventées par Porta vers 1580 ; en tout cas, on en fabriquait en Italie à partir de 1590. Néanmoins, ce n'est guère que vers 1608 que les opticiens hollandais Jansen et Lipperhey commencent à diffuser cette marchandise. Galilée construit lui-même en 1610 une lunette sur la base d'indications assez vagues et applique immédiatement son instrument à l'observation du ciel. Parmi les découvertes de Galilée plus sensationnelles les unes que les autres, il retenons notamment les quatre satellites majeurs circulant autour de Jupiter, qui constituent en quelque sorte un système solaire en miniature, les phases des planètes Mercure et Vénus, l'aspect curieux de Saturne (dû à son anneau, qui ne sera pas résolu par Galilée lui-même), les montagnes et les «mers» de la Lune, les étoiles individuelles de la Voie lactée, les taches solaires. Galilée défendait avec acharnement le système héliocentrique et l'idée que la Terre bougeait en tournant sur elle-même et autour du Soleil, ce que lui valut un très douloureux procès intenté par l'Inquisition Catholique. Les traces de ce procès sont loin d'avoir disparues, même à l'heure actuelle, plus de trois siècles et demi plus tard. En réalité, lorsqu'on considère sans parti pris le procès de Galilée dans ses aspects strictement juridiques, on remarque que Galilée n'apportait pas la preuve de ses affirmations. Il avançait seulement des arguments scientifiques en faveur de la thèse de Copernic qui, s'ils avaient du poids, ne l'emportaient pas de façon décisive sur les arguments des adversaires. Ce n'est que suite aux travaux de Kepler et de Newton que le système héliocentrique s'est imposé.

Johannes Kepler (1571–1630), sans doute le révolutionnaire scientifique le plus important de la Renaissance (Copie d'un portrait perdu de Johannes Kepler, peint en 1610, qui était conservé chez les Bénédictins de Krems)

Arthur Koestler, dans son magnifique essai intitulé «Les Somnambules», soutient que l'astronome Johannes Kepler (1571-1630) est le révolutionnaire le plus important de l'histoire de la Science, sinon dans ses actes du moins dans ses écrits, puisqu'il a osé remplacer les cercles par des ellipses. Kepler publie en 1604 un traité d'optique qui contient une table des réfractions jusqu'à 80° de distance zénithale et la description de la lunette à oculaire convergent. Il traite aussi des ellipses et de la manière de les utiliser pour évaluer les différences de longitude. En 1609 paraît le premier de ses deux ouvrages les plus importants, l'«Astronomia Nova», c'est-à-dire «Astronomie Nouvelle», dans lequel il adopte le système héliocentrique de Copernic, mais va bien au-delà.

En effet, en se servant des observations précises à une minute de degré près accumulées par son maître Brahe, Kepler peut énoncer les deux premières lois du mouvement planétaire, auxquelles il aboutit après des calculs fort complexes. Sa première loi s'énonce ainsi : L'orbite d'une planète est une ellipse dont le Soleil occupe l'un des foyers. Cette loi est en rupture totale avec les conceptions précédentes. La deuxième loi de Kepler, également contenue dans l'«Astronomia Nova», stipule que le rayon vecteur qui joint la Terre au Soleil balaye des aires égales en des temps égaux. C'est la «loi des aires». La troisième loi ne sera publiée que dix années plus tard, en 1619, dans le deuxième de ses deux ouvrages les plus importants. Celui-ci est intitulé «Harmonices Mundi», les «Harmonies du Monde». Elle s'énonce ainsi : Les carrés des temps de révolution de deux planètes autour du Soleil sont entre eux comme les cubes des demi-grands axes. Pour Kepler la pesanteur est une propriété générale de tous les matériaux, et les attractions sont proportionnelles aux quantités de matière mises en cause. Kepler ne fut pas très loin de la formulation exacte des lois de la dynamique, mais il n'arrivait pas à concevoir clairement l'importance dynamique de la variation de la vitesse, autrement dit de l'accélération. Cette formulation fut l'œuvre de Newton, trois quarts de siècle plus tard.

L'aurore de la géodésie moderne

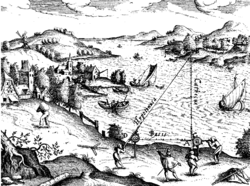Mesure de la largeur d'une rivière au XVI^e siècle. On se sert d'une triangulation au moyen d'un compas de visée pour faire le levé d'une rivière. On détermine la base d'un triangle par mesure directe à l'aide d'une échelle graduée. On vise ensuite en A un objet remarquable B sur l'autre rive, de manière à ce que l'angle en A soit droit. Enfin, à l'autre extrémité de la base (en D) on détermine l'angle que fait DA avec DB. Ainsi on peut facilement calculer la distance AC au moyen du théorème de Pythagore. L'illustration est tirée d'un livre de Hulsius qui à l'époque constituait le traité le plus complet sur le quadrant et son application en astronomie et en topométrie.

Vers 1615 (ou peut-être 1621), le Hollandais Snellius (Willibrord Snell, 1580–1626) tente de vérifier le résultat de Fernel en procédant à une triangulation entre les villes hollandaises Alkmaar et Bergen op Zoom. Il utilise, pour la première fois au monde dans ce type d'opérations, des lunettes de visée. Il mesure une base dans la région de Leyde. Malgré l'emploi d'instruments optiques, ses résultats ne sont pas bons, puisqu'il détermine le degré de méridien trop court d'environ 3,4%. Cette imprécision est surtout causée par la mauvaise conformation de certains triangles retenus. Néanmoins, la méthode est désormais lancée et fournira au cours des décennies suivantes des mesures précises des dimensions de la Terre. Snell n'est pas le premier à avoir effectué une triangulation géodésique. Nous avons déjà cité celle effectuée au Danemark par Tycho Brahe en 1578. En fait, au XVI^e siècle sont apparues de nouvelles méthodes de topométrie, qui se sont développées en s'appuyant sur des méthodes antiques. En 1528, Sebastian Münster propose de faire un levé trigonométrique simple de l'Allemagne, mais vraisemblablement le premier à effectuer une triangulation fut le Hollandais Rainer Gemma Frisius (1508–1555) ; celle-ci constituait en la mesure de la largeur d'une rivière en 1533, en utilisant pour ce faire des triangles quelconques. Néanmoins, c'est à Snell qu'on doit la première triangulation opérée dans le but avoué de déterminer la circonférence de la Terre.

À cette époque, en 1616 très exactement, l'œuvre de Copernic est mise à l'index des livres proscrits par l'Église catholique. Quelques années plus tard, en 1631, le savant français Pierre Gassendi observe le passage de Mercure devant le Soleil. Il fournit donc un argument sérieux, sinon une preuve, que Mercure tourne autour du Soleil et non autour de la Terre, mais deux ans plus tard, en 1633, commence le procès de Galilée.

En 1637, l'astronome anglais Richard Norwood (1590–1675) mesure la distance de Londres à York au moyen d'une chaîne d'arpenteur et par décompte de pas. Il détermine l'angle au centre correspondant à l'arc de méridien associé à cette distance en observant les hauteurs du Soleil à midi, respectivement à Londres et à York. Il trouve pour la distance L(1°) correspondant à un degré de latitude environ 367196 pieds, c'est-à-dire environ 111,92 kilomètres. Ce résultat est trop grand d'un peu moins de 1%. La même année, en 1637, René Descartes publie les lois de l'optique géométrique, surtout la loi de réfraction. Descartes est déjà connu à cette époque pour plusieurs travaux mathématiques importants. En fait, il déduit la loi exacte de la réfraction, qui s'appelle maintenant « loi de Snell-Descartes » en s'appuyant sur une hypothèse inexacte. Pierre de Fermat (1601–1665) accepte le résultat trouvé par Descartes, mais critique ses fondements théoriques. De la sorte, il est amené à énoncer le fameux principe de tautochronisme, dit « principe de Fermat ». Celui-ci exprime que le chemin parcouru par la lumière est toujours tel qu'il correspond à un temps de parcours extrémum.

Mesure de l'angle central par les angles zénithaux (méthode de Riccioli)

L'année après la parution de la loi de la réfraction, Galilée publie ses découvertes fondamentales en mécanique, à savoir celles qui concernent le mouvement uniformément accéléré et la trajectoire des projectiles dans le vide, et il définit la force comme la cause de l'accélération. C'est encore à cette époque que Descartes, Fermat, Roberval et d'autres mettent au point la construction des tangentes aux courbes. Puis, en 1641, Blaise Pascal invente l'arithmomètre, précurseur des machines à calculer et des ordinateurs.

En 1643, Viviani — disciple de Galilée — exécute l'expérience du baromètre de Torricelli (1608–1647), qui met en évidence le poids de l'air et l'existence d'une atmosphère limitée, dont l'expérience de Pascal et Périer, effectuée en 1648 au Puy-de-Dôme, viendra apporter la preuve irréfutable. Tous ces progrès scientifiques vont jouer, à court ou à long terme, un rôle important dans le développement de la géodésie et de la théorie de la figure de la Terre.

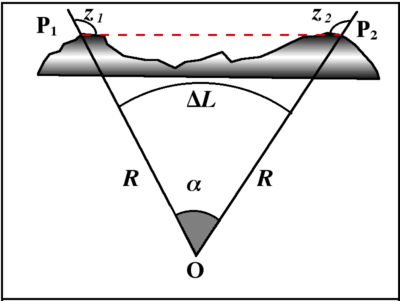
En 1661 le père jésuite Giovanni-Baptista Riccioli reprend la mesure de la longueur L(1°) d'un degré de latitude par une méthode différente de celle d'Eratosthène. Elle se base sur la détermination d'angles zénithaux. Riccioli s'était servi déjà de cette méthode en 1645 en collaboration avec Grimaldi. Elle consiste à mesurer en deux sommets P₁ et P₂, de distance connue P₁P₂, les distances zénithales réciproques z₁ et z₂. La somme des angles du triangle P₁OP₂, où O désigne le centre de la Terre, étant égale à 180°, on déduit que l'angle au centre α est fourni par α = z₁ + z₂ – 180°. Cette méthode, indiquée par Kepler, ne pouvait pas fournir de résultats précis à l'époque, et à ce jour-même elle n'est guère recommandée. En effet, la mesure précise des distances zénithales est rendue délicate par la réfraction atmosphérique négligée à tort par Riccioli. Ainsi, sa valeur de 62900 toises pour L(1°) tombait loin de la valeur exacte. En appliquant un coefficient de réfraction convenable, on peut corriger ce résultat a posteriori et le ramener à une valeur comprise entre 55000 et 57000 toises, sans pouvoir préciser davantage.

Bibliographie

• René Dugas (1950). Histoire de la Mécanique, Éditions du Griffon, Neuchâtel & Éditions Dunod, Paris.
• Jacques Gapaillard (1993). Et pourtant, elle tourne ! (Le mouvement de la Terre), Éditions du Deuil, Paris.
• Arthur Koestler (1960). Les Somnambules, Calman Lévy, Paris.
• René Taton (1994). Histoire générale des sciences (4 volumes), Quadrige/Presses Universitaires de France.
• Arkan Simaan et Joëlle Fontaine, L'Image du monde des Babyloniens à Newton, Adapt Editions, Paris, 1998.

Notes

Liens internes

Voici quelques liens vers des articles ayant trait à l'histoire de la géodésie et la Figure de la Terre :

• Figure de la Terre dans l'Antiquité,
• Figure de la Terre au Moyen Âge,
• Figure de la Terre à la Renaissance,
• Figure de la Terre et gravitation universelle,
• Modèle ellipsoïdal de la Terre,
• Figure de la Terre et les expéditions de Laponie et du Pérou,
• Sphéroïde de Clairaut,
• Masse de la Terre,
• Figure de la Terre et méridienne de Delambre et Méchain,
• Figure de la Terre et histoire du mètre,
• De l'ellipsoïde au géoïde.
• Géoïde
• Révolution copernicienne
• Nicolas Copernic
• Galileo Galilei

Liens externes

• Portail de la géodésie et de la géophysique
• Portail de l’astronomie
• Portail de la géographie