Endomorphisme auto-adjoint

Endomorphisme auto-adjoint

Endomorphisme autoadjoint

En mathématiques et plus précisément en algèbre linéaire, un endomorphisme autoadjoint est un cas particulier d'application linéaire.

Cette propriété s'applique à une application linéaire d'un espace vectoriel dans lui-même ; pour cette raison, l'application est appelée endomorphisme. L'espace vectoriel possède une géométrie particulière, de type euclidien. Elle se généralise sur le corps des complexes et à la dimension infinie. La propriété exprime une compatibilité de l'endomorphisme avec le produit scalaire : il est égal à son adjoint.

En dimension finie, la structure d'un endomorphisme autoadjoint est simple, il existe une base orthonormale de vecteurs propres et les valeurs propres sont toutes réelles. L'adjonction de propriétés de continuité est nécessaire pour le cas de la dimension infinie. Ce cas est largement étudié dans le cadre de l'analyse fonctionnelle.

Les applications de cette propriété structurelle sont nombreuses. En mathématiques, elle permet de résoudre des équations différentielles linéaires, de trouver une base orthogonale pour deux formes quadratiques si l'une est définie positive ou de classifier les quadriques. En physique, elle est utilisée pour résoudre de nombreuses équations aux dérivées partielles comme celle de la corde vibrante ou exprimer le moment d'inertie d'un solide. Elle permet en statistique d'établir la méthode des moindres carrés ou d'étudier un échantillon à l'aide de l'analyse en composantes principales. Enfin de nombreuses méthodes de calcul numérique se fondent sur cette propriété. Ces applications sont traitées dans l'article théorème spectral.

Sommaire

Définition

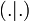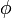Soit E\, un espace vectoriel réel ou complexe, muni d'un produit scalaire noté (.|.)\,. Un tel espace est appelé préhilbertien. Soit a\, un endomorphisme de E\,. La donnée de a\, permet de définir une forme sesquilinéaire \phi \, par l'égalité suivante :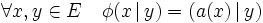

\forall x,y \in E \quad \phi (x\, |\, y) = (a(x) \, |\, y)

S'il existe un endomorphisme souvent noté 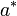a^*\, vérifiant la propriété suivante, alors 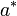a^*\, est appelé l'adjoint de a\,. :

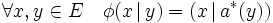
\forall x,y \in E \quad \phi (x\, |\, y) = (x \, |\, a^*(y))

Si E\, est de dimension finie ou s'il est de Hilbert alors tout endomorphisme admet un adjoint.

Définitions — 

  • Un endomorphisme a\, est qualifié d'autoadjoint si et seulement si il est égal à son adjoint, c-à-d si a=a^*\,.
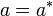  • Un endomorphisme a\, est qualifié d'antiautoadjoint si et seulement si il est opposé à son adjoint, c-à-d si a=-a^*\,.

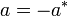Il existe un isomorphisme d'algèbre entre les endomorphismes et les matrices. Il donne lieu aux deux définitions suivantes :

Définitions — 

  • On appelle matrice adjointe d'une matrice carrée 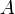A\,, la conjuguée de sa transposée, notée 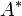A^*\,. On dit qu'une matrice carrée 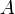A \, est autoadjointe si 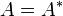A=A^*\,. Si les coefficients sont réels, on parle aussi de matrice symétrique ; si les coefficients sont complexes, on parle aussi de matrice hermitienne.
  • On dit qu'une matrice carrée 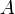A\, est antiautoadjointe si 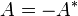A=-A^*\,. Si les coefficients sont réels, on parle aussi de matrice antisymétrique ; si les coefficients sont complexes, on parle aussi de matrice antihermitienne.

Propriétés

Autoadjoint et structure linéaire

Dans ce paragraphe H désigne un espace préhilbertien réel ou complexe. L'ensemble des endomorphismes de H noté L(H) est un espace vectoriel.

Structures de l'ensemble des endomorphismes autoadjoints —  L'ensemble des endomorphismes autoadjoints de H est un sous-espace vectoriel de L(H), image du projecteur p qui à un endomorphisme a associe 1/2 (a + a*). Par définition, un élément du noyau du projecteur p est qualifié d'antisymétrique. Un endomorphisme est antisymétrique si et seulement si son adjoint est égal à son opposé. Les endomorphismes autoadjoints et antisymétriques forment deux sous-espaces vectoriels supplémentaires de H. Si H est de dimension finie n, alors la dimension de l'espace des autoadjoints est n(n + 1)/ 2 et celle des antisymétriques n(n - 1)/2.

En effet, p est manifestement une application linéaire. L'application qui à un endomorphisme associe son adjoint est un endomorphisme involutif, ce qui montre que l'image par p d'une application est autoadjointe. L'image par p d'une application autoadjointe est elle-même, ce qui montre que pop est égal à p et donc que p est un projecteur. Enfin, un calcul direct montre que le noyau de p est égal à l'ensemble des applications antisymétriques. Ces propriétés permettent de déduire que l'ensemble des endomorphismes autoadjoints et bien un sous-espace vectoriel de supplémentaire les antisymétriques. Enfin, une écriture matricielle d'un endomorphisme autoadjoint permet de calculer la dimension.

Autoadjoint et structure bilinéaire

Il existe une relation forte entre les applications linéaires et les formes bilinéaires, dans le cas d'un espace préhilbertien. Elle est plus subtile si H n'est pas complet, car le dual de H n'est pas isomorphe à H. Pour cette raison, H est ici supposé complet, dans ce paragraphe il correspond à un Hilbert. L(H) désigne ici l'ensemble des endomorphismes continus. Dans le cas de la dimension finie tout espace vectoriel muni d'un produit scalaire est un Hilbert et tout endomorphisme est continu.

Il existe un isomorphisme Φ entre L(H) et l'ensemble des formes bilinéaires continues. Cet isomorphisme associe à l'application a la forme Φa définie par :

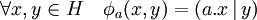
\forall x, y \in H \quad \phi_a (x,y) = (a.x \, |\, y)

Cet isomorphisme engendre naturellement une application linéaire surjective Ψ de L(H) dans l'ensemble des formes quadratiques continues qui, à l'application a, associe Ψa définie par :

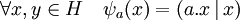
\forall x, y \in H \quad \psi_a (x) = (a.x \, |\, x)

Autoadjoint et forme quadratique —  La restriction Φ à l'ensemble des endomorphismes autoadjoints de H est un isomorphisme sur l'ensemble des formes bilinéaires symétriques (hermitiennes dans le cas complexe) continues. La restriction de Ψ à l'ensemble des autoadjoints est un isomorphisme, le noyau de Ψ est l'ensemble des endomorphismes antisymétriques.

Cette isomorphisme permet d'ajouter deux définitions :

Endomorphisme positif et défini positif —  Un endomorphisme autoadjoint a est dit positif (resp. défini positif) si et seulement si Φa l'est.

Par exemple aoa* est autoadjoint positif et défini positif si et seulement si a est un automorphisme.

Dimension finie

Ici, H désigne un Hilbert de dimension finie n. La structure d'un endomorphisme autoadjoint est simple dans ce cas là :

Réduction d'un endomorphisme autoadjoint —  Soit a un endomorphisme autoadjoint de H. Il existe une base orthonormale de vecteurs propres et les valeurs propres associées sont toutes réelles.

En effet, si λ est une valeur propre et v un vecteur propre associé :

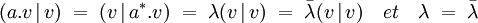
(a.v \, | \, v) \;=\; (v \, | \, a^*.v) \; = \; \lambda (v \, | \, v) \; =\; \bar {\lambda} (v \, | \, v) \quad et \quad \lambda \; =\; \bar {\lambda}

Les valeurs propres sont toutes réelles. L'existence d'une base orthonormale est le propre de tout endomorphisme normal, un autoadjoint correspond donc à un cas particulier de cette démonstration (donnée dans l'article associé).

Dans le cas réel, il est toujours possible de complexifier H en considérant l'espace vectoriel des formes bilinéaires de CxH (ici C désigne l'ensemble des nombres complexes, cet espace est appelé le produit tensoriel de C et de H). Cet espace vectoriel contient une base orthonormale de vecteurs propres de H et de valeurs propres toutes réelles, ce qui démontre la proposition.

Ce théorème possède une réciproque :

Réciproque —  Soit a un endomorphisme admettant une base orthonormale de vecteurs propres et de valeurs propres toutes réelles, alors il est autoadjoint.

Pour s'en convaincre il suffit de développer deux vecteurs v1 et v2 dans une base B (bi) orthonormale de vecteurs propres de valeurs propres (λi). Ici K désigne le corps de H, c'est-à-dire l'ensemble des réels ou des complexes :

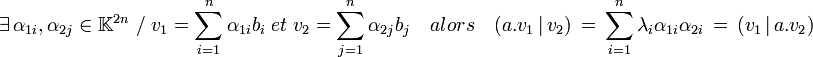
\exists \, \alpha_{1i}, \alpha_{2j} \in \mathbb K^{2n} \; / \; v_1 = \sum_{i=1}^n \alpha_{1i}b_i \; et \; v_2 = \sum_{j=1}^n \alpha_{2j}b_j \quad alors \quad (a.v_1 \, | \, v_2) \, = \, \sum_{i=1}^n \lambda_i\alpha_{1i}\alpha_{2i} \, =\, (v_1 \, | \, a.v_2)

En conséquence une projection est autoadjointe si et seulement si elle est projection orthogonale et il en est de même pour une symétrie.

Ce résultat s'exprime naturellement en termes de forme quadratique. Il prend le nom de théorème spectral, qui possède des versions plus générales en dimension infinie :

Théorème spectral en dimension finie —  Soit E un espace vectoriel de dimension finie sur le corps des réels (resp. des complexes) et Φ, Ψ deux formes bilinéaires symétriques (resp. sesquilinéaire) de E tel que Φ soit définie positive. Alors il existe une base B de E orthonormale pour Φ et orthogonale pour Ψ. Dans cette base, les coefficients de la matrice associée à Ψ sont tous réels.


Tout théorème sur les endomorphismes possède son équivalent sur les matrices :

Formalisme fondé une matrice —  Soit A une matrice symétrique (resp. hermitienne), alors il existe une matrice P orthogonale (resp. unitaire) et une matrice D diagonale dont tous les coefficients sont réels, telles que la matrice A est égale à P.D.P-1 .

Triple norme et endomorphisme autoadjoint

Valeur de la triple norme. —  Soient E un espace euclidien et u un endomorphisme autoadjoint de E.

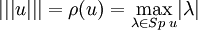
On a : |||u|||=\rho (u)=\underset{\lambda \in Sp\; u}{\max} |\lambda|

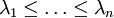Démonstration : soient \mathcal{B}=(e_1,...,e_n) une base orthonormée diagonalisant u (son existence résulte du théorème spectral), et \lambda_1\leq \dots \leq\lambda_n ses valeurs propres.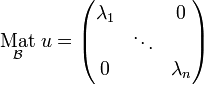

\underset{\mathcal{B}}{\mathrm{Mat}}\;u=\begin{pmatrix} \lambda_1 & &0\\ & \ddots & \\ 0& &\lambda_n\end{pmatrix}

Soit 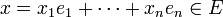x=x_1 e_1+ \cdots +x_n e_n\in E de norme 1.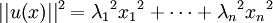

||u(x)||^2={\lambda_1}^2{x_1}^2+ \cdots +{\lambda_n}^2{x_n}^2

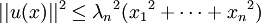
||u(x)||^2\leq {\lambda_n}^2({x_1}^2+ \cdots +{x_n}^2)

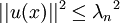
||u(x)||^2\leq {\lambda_n}^2

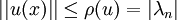
||u(x)||\le\rho(u)=|\lambda_n|

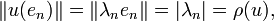
Comme on a : \|u(e_n)\|=\|\lambda_n e_n\|=|\lambda_n|=\rho(u),

on en déduit :

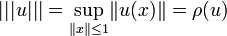
|||u|||=\underset{\|x\|\le 1}{\sup}\|u(x)\|=\rho(u)

Notes et références

Liens externes

Références

  • Serge Lang, Algèbre, Dunod, 2004, 926 p. (ISBN 2100079808) [détail des éditions]
Une référence sur l'algèbre, il traite intégralement la dimension finie
  • Haïm Brezis, Analyse fonctionnelle : théorie et applications [détail des éditions]
Une introduction à l'analyse fonctionnelle, il traite des opérateurs autoadjoints compact et introduit l'opérateur de Fredholm
  • J. P. Aubin Analyse fonctionnelle appliquée Puf 1987 (ISBN 02463822)
Un livre analogue au précédent, cependant simplifié car uniquement le cas des Hilbert réels est traité.
  • Portail des mathématiques Portail des mathématiques
Articles de mathématiques en rapport avec l'algèbre bilinéaire
modifier
Ce document provient de « Endomorphisme autoadjoint ».

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Endomorphisme auto-adjoint de Wikipédia en français (auteurs)

Игры ⚽ Нужен реферат?

Regardez d'autres dictionnaires:

  • Auto-adjoint — Endomorphisme autoadjoint En mathématiques et plus précisément en algèbre linéaire, un endomorphisme autoadjoint est un cas particulier d application linéaire. Cette propriété s applique à une application linéaire d un espace vectoriel dans lui… …   Wikipédia en Français

  • Endomorphisme Autoadjoint — En mathématiques et plus précisément en algèbre linéaire, un endomorphisme autoadjoint est un cas particulier d application linéaire. Cette propriété s applique à une application linéaire d un espace vectoriel dans lui même ; pour cette… …   Wikipédia en Français

  • Endomorphisme autoadjoint — En mathématiques et plus précisément en algèbre linéaire, un endomorphisme autoadjoint ou opérateur hermitien est un endomorphisme d espace de Hilbert qui est son propre adjoint (sur un espace de Hilbert réel on dit aussi endomorphisme… …   Wikipédia en Français

  • Theoreme spectral — Théorème spectral Un ellipsoïde en trois possède autant d axes de symétrie que l espace de dimensions. Ils sont notés ici x, y et z …   Wikipédia en Français

  • Théorème spectral — Un ellipsoïde en trois possède autant d axes de symétrie que l espace de dimensions. Ils sont notés ici x, y et z …   Wikipédia en Français

  • Base propre — Valeur propre, vecteur propre et espace propre Fig. 1. Cette application linéaire déforme la statue de David. Les vecteurs bleus ont pour images les vecteurs verts. Ils gardent la même direction, ce sont des vecteurs propres. La valeur propre… …   Wikipédia en Français

  • Espace propre — Valeur propre, vecteur propre et espace propre Fig. 1. Cette application linéaire déforme la statue de David. Les vecteurs bleus ont pour images les vecteurs verts. Ils gardent la même direction, ce sont des vecteurs propres. La valeur propre… …   Wikipédia en Français

  • Problème aux valeurs propres généralisé — Valeur propre, vecteur propre et espace propre Fig. 1. Cette application linéaire déforme la statue de David. Les vecteurs bleus ont pour images les vecteurs verts. Ils gardent la même direction, ce sont des vecteurs propres. La valeur propre… …   Wikipédia en Français

  • Sous-espace propre — Valeur propre, vecteur propre et espace propre Fig. 1. Cette application linéaire déforme la statue de David. Les vecteurs bleus ont pour images les vecteurs verts. Ils gardent la même direction, ce sont des vecteurs propres. La valeur propre… …   Wikipédia en Français

  • Théorème de Baire-Brenef — Valeur propre, vecteur propre et espace propre Fig. 1. Cette application linéaire déforme la statue de David. Les vecteurs bleus ont pour images les vecteurs verts. Ils gardent la même direction, ce sont des vecteurs propres. La valeur propre… …   Wikipédia en Français

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”