- Distribution (statistique)
-
Loi de probabilité
Une loi de probabilité ou distribution de probabilité a commencé par décrire les répartitions typiques des fréquences d'apparition des résultats d'un phénomène aléatoire. Dans le dernier quart du XXe siècle, on a largement étendu le concept à des domaines où il n'était plus question de fréquences, mais de représentation d'états de connaissance.
Les lois de probabilité sont utilisées en probabilité, et par extension en statistiques, qui sont des branches des mathématiques.
On associe naturellement une loi de probabilité à une variable aléatoire pour décrire la répartition des valeurs qu'elle peut prendre.
Parmi l'ensemble des lois de probabilités possibles, on distingue un certain nombre de familles usuelles qui correspondent à des phénomènes aléatoires simples : lancer de dés, jeu de pile ou face, erreurs de mesures, etc. Combinées entre elles, elles permettent d'élaborer des modélisations de phénomènes aléatoires plus complexes.
Définition informelle
Une loi de probabilité se caractérise de différentes manières. Le plus souvent, on utilise la fonction de répartition pour caractériser une loi. Cela présente l'avantage d'être valable aussi bien pour les lois discrètes que continues. Mais on peut aussi caractériser une loi mixte avec une fonction de répartition. Dans le cas d'une loi continue, on utilise très souvent la densité, alors que dans le cas discret, la donnée des probabilités élémentaires suffit à caractériser la loi en question.
Exemples de lois discrètes
La variable aléatoire X est discrète (l'ensemble de ses valeurs possibles est fini ou dénombrable), on définit alors la probabilité pour chaque valeur n, soit
Loi de Bernoulli
Article détaillé : Loi de Bernoulli.La loi de Bernoulli correspond à un lancer de pile ou face :
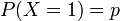 où p = succès
où p = succès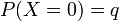 où q = (1-p) = échec
où q = (1-p) = échec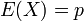
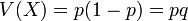
Loi binomiale
Article détaillé : Loi binomiale.- n épreuves de Bernoulli identiques.
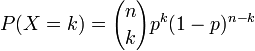 pour tout k de 0 à n, p étant un réel compris entre 0 et 1
pour tout k de 0 à n, p étant un réel compris entre 0 et 1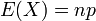
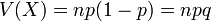 où q = 1 − p
où q = 1 − p
Loi hypergéométrique
Article détaillé : Loi hypergéométrique.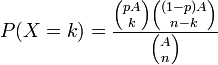 où A est un entier, pA et n des entiers inférieurs à A
où A est un entier, pA et n des entiers inférieurs à A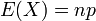
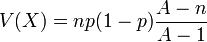
Loi de Poisson
Article détaillé : Loi de Poisson.Loi géométrique
Article détaillé : Loi géométrique.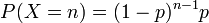 où p est un réel compris entre 0 et 1 et n un entier non nul.
où p est un réel compris entre 0 et 1 et n un entier non nul.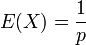
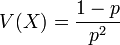
Exemples de lois à densité
Article détaillé : Densité de probabilité.Une variable aléatoire réelle
 possède une densité de probabilité
possède une densité de probabilité 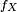 , si pour tous nombres réels
, si pour tous nombres réels 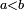 on a
on aOn dit aussi alors que la loi
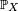 de
de  possède une densité, ou bien est à densité. D'une manière équivalente, on dit que
possède une densité, ou bien est à densité. D'une manière équivalente, on dit que 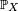 est absolument continue par rapport à la mesure de Lebesgue.
est absolument continue par rapport à la mesure de Lebesgue.En conséquence,
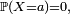 pour tout nombre réel
pour tout nombre réel 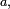 et la fonction de répartition
et la fonction de répartition 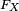 de
de  est continue. On a plus précisément
est continue. On a plus précisémentLes variables aléatoires à densité sont parfois appelées variables continues.
Loi uniforme
Article détaillé : Loi uniforme continue.Loi uniforme continue sur un intervalle borné [a; b] :
Loi normale
Article détaillé : Loi normale.Loi exponentielle
Article détaillé : Loi exponentielle.Loi logistique
Article détaillé : Loi logistique.Loi de Cauchy
Article détaillé : Loi de Cauchy.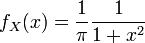
La loi de Cauchy n'admet aucun moment (donc ni moyenne ni variance, entre autres).
Loi de Tukey-Lambda
La Loi de Tukey-Lambda est connue de façon implicite par la distribution de ses quantiles :
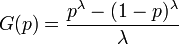
elle a par la suite été généralisée.
Définition mathématique
En théorie des probabilités, une loi (ou mesure) de probabilité est une mesure positive
 sur un espace mesurable
sur un espace mesurable 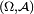 , telle que
, telle que 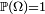 . Le triplet
. Le triplet 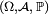 est appelé espace probabilisé.
est appelé espace probabilisé.Définition — Soit une variable aléatoire réelle sur l'espace probabilisé
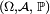 , c'est-à-dire une fonction mesurable
, c'est-à-dire une fonction mesurable 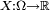 (l'ensemble
(l'ensemble 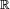 étant muni de sa tribu borélienne
étant muni de sa tribu borélienne 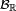 ). On appelle loi (de probabilité) de la variable aléatoire
). On appelle loi (de probabilité) de la variable aléatoire  la mesure de probabilité
la mesure de probabilité 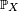 définie sur l'espace mesurable
définie sur l'espace mesurable 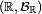 par :
par :pour tout borélien
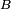 de
de 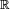 . On dit parfois que
. On dit parfois que 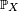 est la mesure image de
est la mesure image de  par
par  .
.Bien évidemment, deux variables aléatoires réelles
 et
et 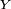 ont même loi si
ont même loi si 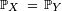 (égalité de fonctions). Cela se réécrit
(égalité de fonctions). Cela se réécritou bien encore
Plus généralement, deux variables aléatoires réelles
 et
et 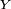 ont même loi si
ont même loi sipour toute fonction
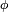 de
de 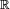 dans
dans 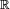 telle qu'au moins un des deux termes de l'égalité ait un sens.
telle qu'au moins un des deux termes de l'égalité ait un sens.Caractérisation de la loi de probabilité d'une variable aléatoire réelle
En probabilité, il est crucial de pouvoir vérifier que deux variables aléatoires (réelles ou pas) ont la même loi de manière la plus économique possible, or les caractérisations ci-dessus exigent de vérifier des familles d'identités beaucoup trop riches (pour tout borélien B, pour toute fonction borélienne φ ...). Une solution plus ergonomique est fournie par les notions de fonction de répartition, ou de fonction caractéristique.
Caractérisation à l'aide de la fonction de répartition
La loi d'une variable aléatoire réelle est caractérisée par sa fonction de répartition : deux variables aléatoires réelles
 et
et 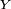 ont même loi si elles ont même fonctions de répartition, i.e. si
ont même loi si elles ont même fonctions de répartition, i.e. siAinsi il suffit de vérifier l'égalité caractéristique pour une famille réduite de boréliens
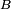 très particuliers, les boréliens de la forme
très particuliers, les boréliens de la forme ![\scriptstyle\ ]-\infty,x],\](/pictures/frwiki/49/1711bb012e78b43510de09326a6dd123.png) pour démontrer les égalités
pour démontrer les égalités 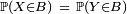 et
et ![\scriptstyle\ \mathbb{E}\left[\phi(X)\right]\ =\ \mathbb{E}\left[\phi(Y)\right]](/pictures/frwiki/48/0c50fd143e72130628f59daf45615b33.png) en toute généralité. Ce résultat crucial est une conséquence du Lemme de classe monotone dû à Wacław Sierpiński.
en toute généralité. Ce résultat crucial est une conséquence du Lemme de classe monotone dû à Wacław Sierpiński.Caractérisation à l'aide de la fonction caractéristique
La loi d'une variable aléatoire réelle est caractérisée par sa fonction caractéristique : deux variables aléatoires réelles
 et
et 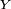 ont même loi si elles ont même fonction caractéristique, i.e. si
ont même loi si elles ont même fonction caractéristique, i.e. siAinsi il suffit de vérifier l'égalité caractéristique pour une famille réduite de fonctions
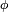 très particulières, les fonctions de la forme
très particulières, les fonctions de la forme 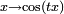 et
et 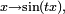 pour démontrer que
pour démontrer que  et
et 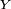 ont même loi.
ont même loi.Caractérisation à l'aide de la transformée de Laplace
La loi d'une variable aléatoire réelle positive ou nulle est caractérisée par sa transformée de Laplace : deux variables aléatoires réelles positives ou nulles
 et
et 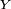 ont même loi si elles ont même transformée de Laplace, i.e. si
ont même loi si elles ont même transformée de Laplace, i.e. siCaractérisation à l'aide de la fonction génératrice
La loi d'une variable aléatoire à valeurs entières positives ou nulles est caractérisée par sa fonction génératrice : deux variables aléatoires à valeurs entières positives ou nulles
 et
et 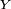 ont même loi si elles ont même fonction génératrice, i.e. si
ont même loi si elles ont même fonction génératrice, i.e. siClassification des lois de probabilités sur la droite réelle
Les lois énumérées dans cet article sont des mesures de probabilités sur
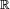 . Ces lois apparaissent en général dans les applications comme les lois de probabilité de certaines variables aléatoires réelles. Les lois énumérées dans cet article sont de deux types :
. Ces lois apparaissent en général dans les applications comme les lois de probabilité de certaines variables aléatoires réelles. Les lois énumérées dans cet article sont de deux types :- lorsque la loi de la variable aléatoire
 est portée (i.e.
est portée (i.e. 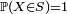 ) par un ensemble
) par un ensemble  fini ou dénombrable, on parle de loi discrète. D'un point de vue pratique, les calculs de probabilités ou bien d'espérances liées à
fini ou dénombrable, on parle de loi discrète. D'un point de vue pratique, les calculs de probabilités ou bien d'espérances liées à  font alors intervenir des calculs de sommes finies ou de séries:
font alors intervenir des calculs de sommes finies ou de séries:
![\mathbb{P}\left(X\in A\right)=\sum_{x\in A\cap S}\ \mathbb{P}\left(X=x\right),\qquad\mathbb{E}\left[\phi(X)\right]=\sum_{x\in S}\ \phi(x)\mathbb{P}\left(X=x\right).](/pictures/frwiki/51/3383874afdfabb7a44549f5c24c87a9b.png)
- Pour une variable discrète, on peut choisir comme ensemble
 l'ensemble des réels
l'ensemble des réels  tels que
tels que 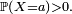
- lorsque la loi de
 est absolument continue par rapport à la mesure de Lebesgue sur
est absolument continue par rapport à la mesure de Lebesgue sur 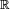 , ou bien, d'une manière équivalente, lorsque la fonction de répartition de
, ou bien, d'une manière équivalente, lorsque la fonction de répartition de  est localement absolument continue, on parle de variable ou de loi absolument continue, ou bien de variable ou de loi à densité. Dans ce cas, en vertu du Théorème de Radon-Nikodym, la mesure
est localement absolument continue, on parle de variable ou de loi absolument continue, ou bien de variable ou de loi à densité. Dans ce cas, en vertu du Théorème de Radon-Nikodym, la mesure 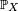 (et la variable
(et la variable  ) possèdent une densité de probabilité (notons là
) possèdent une densité de probabilité (notons là 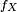 ) par rapport à la mesure de Lebesgue. D'un point de vue pratique, les calculs de probabilités ou bien d'espérances liées à
) par rapport à la mesure de Lebesgue. D'un point de vue pratique, les calculs de probabilités ou bien d'espérances liées à  font alors intervenir des calculs d'intégrales:
font alors intervenir des calculs d'intégrales:
![\mathbb{P}\left(X\in A\right)=\int_{A}\ f_X(x)\,dx,\qquad\mathbb{E}\left[\phi(X)\right]=\int_{\mathbb{R}}\ \phi(x)\ f_X(x)\,dx.](/pictures/frwiki/56/8afc23451ff6cf9d74e0fa62a2867023.png)
- Une variable à densité
 vérifie
vérifie 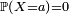 pour tout nombre réel
pour tout nombre réel 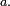 Toutefois, cette dernière propriété, qui oppose les variables à densité aux variables discrètes, n'est pas caractéristique des variables à densité.
Toutefois, cette dernière propriété, qui oppose les variables à densité aux variables discrètes, n'est pas caractéristique des variables à densité.
Il existe d'autres types de variables aléatoires réelles :
- la loi d'une variable aléatoire
 peut très bien n'être ni discrète ni absolument continue. Elle peut, par exemple, être un mélange des deux : si la loi de la durée de vie (avant panne)
peut très bien n'être ni discrète ni absolument continue. Elle peut, par exemple, être un mélange des deux : si la loi de la durée de vie (avant panne) 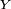 d'un composant d'un certain type suit la loi exponentielle d'espérance 1 (an), et si par mesure de sécurité, on décide de remplacer chaque composant en cas de panne, mais aussi dès que le composant atteint l'age d'un an, même s'il n'est pas encore tombé en panne, alors la durée d'utilisation
d'un composant d'un certain type suit la loi exponentielle d'espérance 1 (an), et si par mesure de sécurité, on décide de remplacer chaque composant en cas de panne, mais aussi dès que le composant atteint l'age d'un an, même s'il n'est pas encore tombé en panne, alors la durée d'utilisation  du composant (
du composant (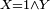 ) n'est ni discrète ni absolument continue. En effet les calculs de probabilités ou bien d'espérances liées à
) n'est ni discrète ni absolument continue. En effet les calculs de probabilités ou bien d'espérances liées à  font alors intervenir des calculs d'intégrales et de sommes :
font alors intervenir des calculs d'intégrales et de sommes :
- dans le cas précédent, la fonction de répartition de la durée d'utilisation
 est discontinue en 1. En général, la fonction de répartition de
est discontinue en 1. En général, la fonction de répartition de  est discontinue en
est discontinue en  si et seulement si
si et seulement si 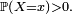 On voit que les variables à densité ont des fonctions de répartitions localement absolument continues, donc, a fortiori, continues sur
On voit que les variables à densité ont des fonctions de répartitions localement absolument continues, donc, a fortiori, continues sur 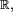 alors que les fonctions de répartition des variables discrètes et du mélange évoqué précédemment possèdent des discontinuités sur la droite réelle. Le tableau est encore compliqué par l'existence de variables aléatoires dont la fonction de répartition est continue sur
alors que les fonctions de répartition des variables discrètes et du mélange évoqué précédemment possèdent des discontinuités sur la droite réelle. Le tableau est encore compliqué par l'existence de variables aléatoires dont la fonction de répartition est continue sur 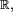 mais pas absolument continue, et qui ne sont donc pas à densité. C'est le cas, par exemple, de
mais pas absolument continue, et qui ne sont donc pas à densité. C'est le cas, par exemple, de
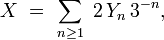
- où les
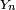 désignent une suite de variables de Bernoulli indépendantes de paramètres 0,5.
désignent une suite de variables de Bernoulli indépendantes de paramètres 0,5.  est un nombre dont on tire le développement triadique à pile ou face : à chaque pile on ajoute le chiffre 2, et à chaque face le chiffre 0, excluant ainsi le chiffre 1. La fonction de répartition de
est un nombre dont on tire le développement triadique à pile ou face : à chaque pile on ajoute le chiffre 2, et à chaque face le chiffre 0, excluant ainsi le chiffre 1. La fonction de répartition de  est l'escalier de Cantor. Une telle variable doit-elle être appelée continue (sa fonction de répartition l'est), ou pas (elle n'a pas de densité de probabilité) ? Le débat n'est pas très aigu, car ce type de variables apparait rarement dans les applications.
est l'escalier de Cantor. Une telle variable doit-elle être appelée continue (sa fonction de répartition l'est), ou pas (elle n'a pas de densité de probabilité) ? Le débat n'est pas très aigu, car ce type de variables apparait rarement dans les applications.
Histoire
L'allure générale des lois de probabilité usuelles fut au début observée empiriquement, puis on en formalisa la définition dans le cadre de la théorie des probabilités en mathématiques.
Maximum d'entropie
Les lois de probabilité usuelles sont souvent classées par familles dépendant d'un paramètre. La loi normale par exemple est paramétrée par sa moyenne et son écart type. La plupart des familles usuelles de lois de probabilités sont celles offrant le maximum d'entropie (l'entropie est une mesure de l'information moyenne d'une source, au sens de Claude Shannon, donc le plus d'information) sous contraintes :
- La distribution normale par exemple est celle d'entropie maximale parmi toutes les lois possibles ayant même moyenne et même écart type.
- La distribution exponentielle est celle d'entropie maximale parmi les lois portées par
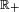 et ayant la même moyenne.
et ayant la même moyenne. - Les lois scalantes comme celle de Zipf ou de Mandelbrot sont d'entropie maximale parmi celles auxquelles on impose la valeur du logarithme d'une moyenne, c'est-à-dire un ordre de grandeur.
En quelque sorte, ces lois ne contiennent pas plus d'information que ce qui est obligatoire. Ce sont les moins prévenues de toutes les lois compatibles avec les observations ou les contraintes, et donc les seules admissibles objectivement comme distributions de probabilités a priori lorsque ces valeurs sont imposées et seules connues. Cette propriété joue un grand rôle dans les méthodes bayésiennes.
Exemples de distribution
- Distribution de Gauss
- Distribution de Poisson
- Distribution de Lévy
- Distribution de Lévy tronquée
- Distribution de Dirac
- Distribution de Gumbel
- Distribution de Boltzmann
- Distribution de Bose-Einstein
- Distribution de Weibull
- Distribution de Dirichlet
Voir aussi
Liens connexes
- Portail des probabilités et des statistiques
Catégories : Loi de probabilité | Statistiques | Probabilités
Wikimedia Foundation. 2010.

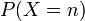
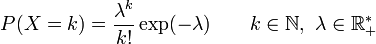
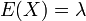
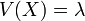
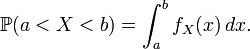
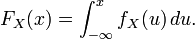
![f_X (x) = \left\{\begin{matrix} \frac{1}{b-a}\ \mathrm{si}\ x \in [a;b] \\ 0\ \mathrm{sinon} \end{matrix}\right.](/pictures/frwiki/57/9f9e21e3bc2ec04dd03901a2307154f5.png)
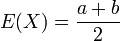
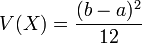
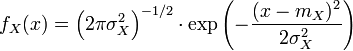
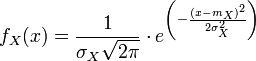
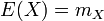
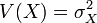
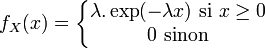
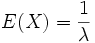
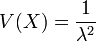
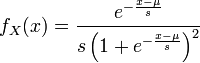
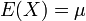
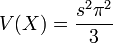
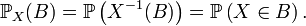
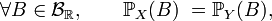
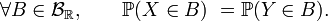
![\mathbb{E}\left[\phi(X)\right]\ = \mathbb{E}\left[\phi(Y)\right]](/pictures/frwiki/52/422abfdc7c17520b9b63c57ef6319072.png)
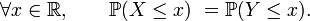
![\forall t\in\mathbb{R},\qquad\mathbb{E}\left[e^{itX}\right]\ = \mathbb{E}\left[e^{itY}\right].](/pictures/frwiki/48/0327c4d61fbe62656f5ae75fea3dce9e.png)
![\forall \lambda>0,\qquad\mathbb{E}\left[e^{-\lambda X}\right]\ = \mathbb{E}\left[e^{-\lambda Y}\right].](/pictures/frwiki/48/0e0b5886f280c174ae103b64b3ba583a.png)
![\forall s\in\mathbb{R},\qquad\mathbb{E}\left[s^{X}\right]\ = \mathbb{E}\left[s^{Y}\right].](/pictures/frwiki/101/e1c22c05e393201d965072b01d2ddebc.png)
![\mathbb{P}\left(X\in A\right)=e^{-1}1_A(1)+\int_{A}\ e^{-x}\,1_{[0,1]}(x)\,dx,\qquad\mathbb{E}\left[\phi(X)\right]=e^{-1}\phi(1)+\int_{0}^1\ \phi(x)\ e^{-x}\,dx.](/pictures/frwiki/48/0769404099bad8f2b248be958c8ec541.png)