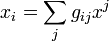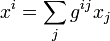Transformation contraco
- Transformation contraco
-
Transformation contraco
On obtient (ou transforme) les composantes contravariantes d'un tenseur en composantes covariantes au moyen du tenseur métrique :
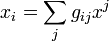
Étant donné que gij est la matrice inverse de gij (démonstration ici), on a
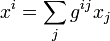
Remarques
- Avec la convention d'Einstein, on sous-entend le symbole Σ dès qu'un indice figure à la fois en haut et en bas. On écrit ainsi xi = gijxj, et xi = gijxj.
- Il existe une convention plus radicale utilisée par certains auteurs suivant laquelle on omet également le tenseur métrique dès lors qu'il intervient dans une contraction. Ainsi, à la place de aibi = gijaibj, on écrit aibi.
- La transformation contraco peut être appliquée à plusieurs indices d'un tenseur d'ordre quelconque. Par exemple aij = gikgjlakl.
Catégorie : Calcul tensoriel
Wikimedia Foundation.
2010.
Contenu soumis à la licence CC-BY-SA. Source : Article Transformation contraco de Wikipédia en français (auteurs)
Regardez d'autres dictionnaires:
Projet:Mathématiques/Liste des articles de mathématiques — Cette page n est plus mise à jour depuis l arrêt de DumZiBoT. Pour demander sa remise en service, faire une requête sur WP:RBOT Cette page recense les articles relatifs aux mathématiques, qui sont liés aux portails de mathématiques, géométrie ou… … Wikipédia en Français
Tenseur metrique — Tenseur métrique Articles scientifiques sur les tenseurs Généralités Tenseur Mathématiques Tenseur (mathématiques) Produit tensoriel ... de deux modules ... de deux applications linéaires Algèbre tensorielle Champ tensoriel Espace tensoriel … Wikipédia en Français
Tenseur métrique — En géométrie et plus particulièrement en géométrie différentielle, le tenseur métrique est un tenseur d ordre 2 qui est utilisé pour la mesure des distances et des angles. Il généralise le théorème de Pythagore. Dans un système de coordonnées… … Wikipédia en Français
Contraction Tensorielle — En algèbre multilinéaire, la contraction est un procédé de calcul sur les tenseurs faisant intervenir la dualité. En coordonnées elle se représente de façon très simple en utilisant les notations d Einstein et consiste à faire une somme sur un… … Wikipédia en Français
Contraction tensorielle — En algèbre multilinéaire, la contraction est un procédé de calcul sur les tenseurs faisant intervenir la dualité. En coordonnées elle se représente de façon très simple en utilisant les notations d Einstein et consiste à faire une somme sur un… … Wikipédia en Français
Inverse De La Matrice Du Tenseur Métrique — Articles scientifiques sur les tenseurs Généralités Tenseur Mathématiques Tenseur (mathématiques) Produit tensoriel ... de deux modules ... de deux applications linéaires Algèbre tensorielle Champ tensoriel Espace tensoriel … Wikipédia en Français
Inverse de la matrice du tenseur metrique — Inverse de la matrice du tenseur métrique Articles scientifiques sur les tenseurs Généralités Tenseur Mathématiques Tenseur (mathématiques) Produit tensoriel ... de deux modules ... de deux applications linéaires Algèbre tensorielle Champ… … Wikipédia en Français
Inverse de la matrice du tenseur métrique — Articles scientifiques sur les tenseurs Généralités Tenseur Mathématiques Tenseur (mathématiques) Produit tensoriel ... de deux modules ... de deux applications linéaires Algèbre tensorielle Champ tensoriel Espace tensoriel … Wikipédia en Français