Vecteur de killing conforme

Vecteur de Killing conforme

En géométrie riemannienne, un vecteur de Killing conforme ou un champ de vecteurs de Killing conforme ou un champ conforme est un champ de vecteurs correspondant à une variation infinitésimale d'une isotopie conforme pour une métrique pseudoriemannienne. En l'absence d'orbites périodiques, après une transformation conforme correctement choisie sur la métrique, le champ de vecteurs devient un champ de vecteurs de Killing ; cela peut être réalisé au moins localement. Sans être forcément de Killing un champ conforme possède des propriétés proches.

Les vecteurs de Killing interviennent notamment en relativité générale.

En géométrie symplectique, les champs de dilatation en sont des équivalents.

Définition

Etant donnée une métrique pseudoriemannienne g sur une variété différentielle M, une application conforme de M est un difféomorphisme 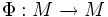$\Phi:M\rightarrow M$ tel que $Φ * g = f . g$ où f est une fonction strictement positive. La métrique $Φ * g$ est dite conforme à g. Les isométries riemanniennes sont des cas particuliers d'applications conformes. L'ensemble des applications conformes forme un sous-groupe du groupe des difféomorphismes de M. Avec les bonnes structures, il en est un sous-groupe de Lie.

On définit un vecteur de Killing conforme comme un champ de vecteurs X dont le flot est constitué d'applications conformes. Ici, le flot est seulement localement défini : X n'est pas nécessairement complet. Cette propriété équivaut à ce que la dérivée de Lie 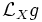$\mathcal{L}_Xg$ soit proportionnelle à g. Les vecteurs de Killing sont donc par définition les variations premières des isotopies conformes (isotopie d'applications conformes). Plus exactement, si $g t$ est une isotopie conforme, alors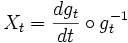

$X_t=\frac{dg_t}{dt}\circ g_t^{-1}$

est un champ de vecteurs de Killing dépendant d'un paramètre réel t. L'identité ci-dessus donne une correspondance biunivoque entre les isotopies conformes et les champs de vecteurs de Killing conformes dépendant d'un paramètre réel.

L'ensemble des vecteurs de Killing conformes est stable par addition et multiplication par des fonctions. Il forme un sous-module de l'espace des champs de vecteurs. Le crochet de Lie de deux vecteurs de Killing conformes est un vecteur de Killing conforme. Donc, l'ensemble des vecteurs de Killing forment une sous-algèbre de Lie de l'algèbre des champs de vecteurs. Cette sous-algèbre de Lie peut être vue comme l'algèbre de Lie du groupe de Lie des applications conformes de $(M, g)$ . Ce groupe est de dimension infinie.

Équation dans une carte locale

Un vecteur de Killing ξ est défini par l'équation

D a ξ b + D b ξ a = 0

où D est la dérivation convariante associée à la métrique. Lors d'une transformation conforme, la métrique g est transformée selon

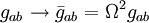$g_{ab} \to \bar g_{ab} = \Omega^2 g_{ab}$ ,

où Ω est une fonction ne s'annulant pas. À l'aide de ces définitions, il est possible de calculer l'équivalent de l'équation de Killing à laquelle obéit le vecteur ξ, mais en utilisant la dérivation covariante 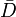$\bar D$ associée à la nouvelle métrique 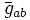$\bar g_{ab}$ . On trouve ainsi

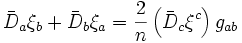$\bar D_a \xi_b + \bar D_b \xi_a = \frac{2}{n} \left(\bar D_c \xi^c\right) g_{ab}$ ,

où n est la dimension de l'espace considéré.

Démonstration

À partir de la nouvelle métrique 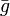$\bar g$ , il est possible de calculer les nouveaux symboles de Christoffel, qui s'écrivent :

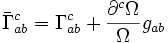$\bar \Gamma^{c}_{ab} = \Gamma^c_{ab} + \frac{\partial^c \Omega}{\Omega} g_{ab}$ .

La nouvelle équation de Killing de réécrit donc

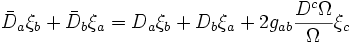$\bar D_a \xi_b + \bar D_b \xi_a = D_a \xi_b + D_b \xi_a + 2 g_{ab} \frac{D^c \Omega}{\Omega} \xi_c$ .

En prenant la trace de cette équation, et en se souvenant que la divergence d'un vecteur de Killing est nulle, il vient

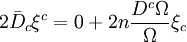$2 \bar D_c \xi^c = 0 + 2 n \frac{D^c \Omega}{\Omega} \xi_c$ .

Le membre de droite de la nouvelle équation de Killing peut ainsi être modifié en

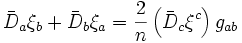$\bar D_a \xi_b + \bar D_b \xi_a = \frac{2}{n} \left(\bar D_c \xi^c \right) g_{ab}$ .

Propriété

Si v et w sont deux vecteurs tangents en p et orthogonaux pour la métrique g précédemment introduite, on a, pour tout champ de vecteurs de Killing conforme :

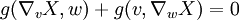
$g(\nabla_vX,w)+g(v,\nabla_wX)=0$

Si X est un champ de vecteurs de Killing, l'identité précédente reste plus généralement vraie pour tous vecteurs v et w tangents en p.

Explications

En effet, on est en droit de considérer deux champs de vecteurs V et W valant respectivement v et w en p. Comme la connexion de Levi-Civita est par définition métrique, la dérivée de g(V,W) dans la direction de X peut s'écrire :

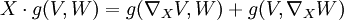$X\cdot g(V,W)=g(\nabla_XV,W)+g(V,\nabla_XW)$ .

Le calcul de cette dérivée peut être obtenu en utilisant la dérivation de Lie. Comme la connexion est sans torsion, on trouve :

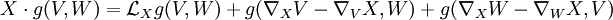
$X\cdot g(V,W)=\mathcal{L}_Xg(V,W)+g(\nabla_XV-\nabla_VX,W)+g(\nabla_XW-\nabla_WX,V)$

En combinant les deux identités ci-dessus, on obtient :

$g(\nabla_VX,W)+g(V,\nabla_WX)=\mathcal{L}_Xg(V,W)$

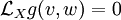Cette identité peut être évaluée au point p. Comme X est un vecteur de Killing conforme, $\left[\mathcal{L}_Xg\right]_p$ est propostionnelle à g_p. Les vecteurs v et w étant orthogonaux pour g, on a : $\mathcal{L}_Xg(v,w)=0$ , et donc :

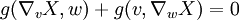
$g(\nabla_vX,w)+g(v,\nabla_wX)=0$

En particulier, si v est un vecteur isotropique, $g (v, v) = 0$ , alors v est orthogonal à lui-même. Pour tout champ de vecteurs de Killing conforme X, on a :

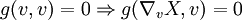
$g(v,v)=0\Rightarrow g(\nabla_vX,v)=0$

En particulier si c est une géodésique de vecteur vitesse isotrope, alors le produit scalaire de X avec le vecteur vitesse est constant :

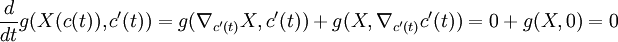
$\frac{d}{dt}g(X(c(t)),c'(t))=g(\nabla_{c'(t)}X,c'(t))+g(X,\nabla_{c'(t)}c'(t))=0+g(X,0)=0$

Cette propriété de conservation intervient notamment en géométrie lorentzienne pour traiter des géodésiques de genre lumière.

Voici une autre façon de l'obtenir en utilisant l'expression des champs de vecteurs de Killing conformes dans les cates locales. Si l'on note 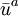$\bar u^a$ le vecteur tangent d'un géodésique associée à la métrique 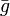$\bar g$ , alors en contractant l'équation à laquelle obéissent les vecteurs de Killing conformes avec 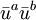$\bar u^a \bar u^b$ , on obtient

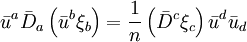$\bar u^a \bar D_a \left(\bar u^b \xi_b \right) = \frac{1}{n} \left(\bar D^c \xi_c\right) \bar u^d \bar u_d$ .

Dans le cas d'un géodésique de genre temps, la norme 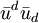$\bar u^d \bar u_d$ est non nulle et la quantité 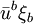$\bar u^b \xi_b$ n'est en général pas conservée. Par contre, dans le cas d'une géodésique de genre lumière, où 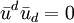$\bar u^d \bar u_d = 0$ , alors la quantité 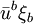$\bar u^b \xi_b$ est conservée.

Voir aussi

Référence

(en) Robert M. Wald, General Relativity, University of Chicago Press, 1984, 498 pages (ISBN 0226870332), pages 443 et 444.

Portail de la géométrie

Ce document provient de « Vecteur de Killing conforme ».

Catégories : Géométrie riemannienne | Champ de vecteurs

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Vecteur de killing conforme de Wikipédia en français (auteurs)

Игры ⚽ Нужен реферат?

Regardez d'autres dictionnaires:

Vecteur de Killing conforme — En géométrie riemannienne, un vecteur de Killing conforme ou un champ de vecteurs de Killing conforme ou un champ conforme est un champ de vecteurs correspondant à une variation infinitésimale d une isotopie conforme pour une métrique… … Wikipédia en Français
Vecteur de killing — En mathématiques, un vecteur de Killing[1], ou champ de Killing, est un champ vectoriel sur une variété riemannienne qui conserve la métrique de cette variété. Le nom de vecteur de Killing est donné en l honneur du mathématicien allemand Wilhelm… … Wikipédia en Français
Vecteur de Killing — En mathématiques, un vecteur de Killing[1], ou champ de Killing, est un champ vectoriel sur une variété riemannienne qui conserve la métrique de cette variété. Le nom de vecteur de Killing est donné en l honneur du mathématicien allemand Wilhelm… … Wikipédia en Français
Champ De Killing — Vecteur de Killing En mathématiques, un vecteur de Killing[1], ou champ de Killing, est un champ vectoriel sur une variété riemannienne qui conserve la métrique de cette variété. Le nom de vecteur de Killing est donné en l honneur du… … Wikipédia en Français
Champ de Killing — Vecteur de Killing En mathématiques, un vecteur de Killing[1], ou champ de Killing, est un champ vectoriel sur une variété riemannienne qui conserve la métrique de cette variété. Le nom de vecteur de Killing est donné en l honneur du… … Wikipédia en Français
Champ de killing — Vecteur de Killing En mathématiques, un vecteur de Killing[1], ou champ de Killing, est un champ vectoriel sur une variété riemannienne qui conserve la métrique de cette variété. Le nom de vecteur de Killing est donné en l honneur du… … Wikipédia en Français
Projet:Mathématiques/Liste des articles de mathématiques — Cette page n est plus mise à jour depuis l arrêt de DumZiBoT. Pour demander sa remise en service, faire une requête sur WP:RBOT Cette page recense les articles relatifs aux mathématiques, qui sont liés aux portails de mathématiques, géométrie ou… … Wikipédia en Français
Liste des articles de mathematiques — Projet:Mathématiques/Liste des articles de mathématiques Cette page recense les articles relatifs aux mathématiques, qui sont liés aux portails de mathématiques, géométrie ou probabilités et statistiques via l un des trois bandeaux suivants … Wikipédia en Français
Géométrie différentielle des surfaces — En mathématiques, la géométrie différentielle des surfaces est la branche de la géométrie différentielle qui traite des surfaces (les objets géométriques de l espace usuel E3, ou leur généralisation que sont les variétés de dimension 2), munies… … Wikipédia en Français
TEMPS — Chacun sait à quel aspect de son expérience répond le mot de temps; mais aucune définition de la notion correspondante n’a reçu jusqu’ici, chez les savants comme chez les philosophes, une approbation unanime. Sensible à cette difficulté qu’il… … Encyclopédie Universelle

Dictionnaires et Encyclopédies sur 'Academic'

Vecteur de killing conforme