Inversion (géométrie)

Pour les articles homonymes, voir Inversion.

Définition générale dans le cadre d’un espace affine euclidien

Soit un espace affine euclidien, un point de et , alors pour tout point de distinct de , il existe un unique point de tel que :

• , et sont alignés ;
• (produit des valeurs algébriques).

On peut ainsi définir l’inversion de centre et de rapport comme l’application de dans lui-même qui, à un point M, associe l’unique point correspondant aux caractéristiques précédentes.

Démonstration de l’existence et de l’unicité de

Analyse

Supposons qu’un tel point existe. Alors , et sont alignés. Ainsi, .

Et comme , car pour des points alignés le produit scalaire est identique au produit des valeurs algébriques, on a :

.

Puisque est distinct de , on peut écrire :

.

Synthèse

Le point satisfait bien aux contraintes, et de par notre analyse il est le seul.

Remarque

Pourquoi n’avons nous pas simplement défini une inversion à partir de la formule précédente ? Parce qu’en fait la définition reste valable dans un espace affine quelconque, dès lors que l’on dispose d’une valeur algébrique sur les droites...

 

Propriétés

• Une inversion de rapport non-nul est bijective.
• Une inversion est une involution : elle est sa propre réciproque.
• On appelle sphère d’inversion (ou cercle d’inversion dans le plan) la sphère de centre et de rayon . Elle est toujours globalement invariante, et elle est invariante point par point lorsque le rapport est positif.
• Les hyperplans passant par sont aussi des invariants globaux.

Le principal intérêt des inversions est la propriété de conservation hyperplans/hypersphères (ou des droites/cercles dans le plan) :

Théorème

L’ensemble constitué par les hypersphères et les hyperplans est stable par inversion. Autrement dit, l’image, par une inversion, d’une hypersphère ou d’un hyperplan, est une hypersphère ou un hyperplan. Mais il est parfaitement possible que l’image d’une hypersphère (resp. d’un hyperplan) soit un hyperplan (resp. une hypersphère).

Dans le plan

Dans le plan affine euclidien

Dans le plan affine euclidien, l’inverse d’un point est constructible au compas lorsqu’on connait le cercle d'inversion, ce qui permet de démontrer le :

Théorème de Mohr et Mascheroni

Toute construction à la règle et au compas peut se faire uniquement au compas (à l’exception des tracés des portions de droites).

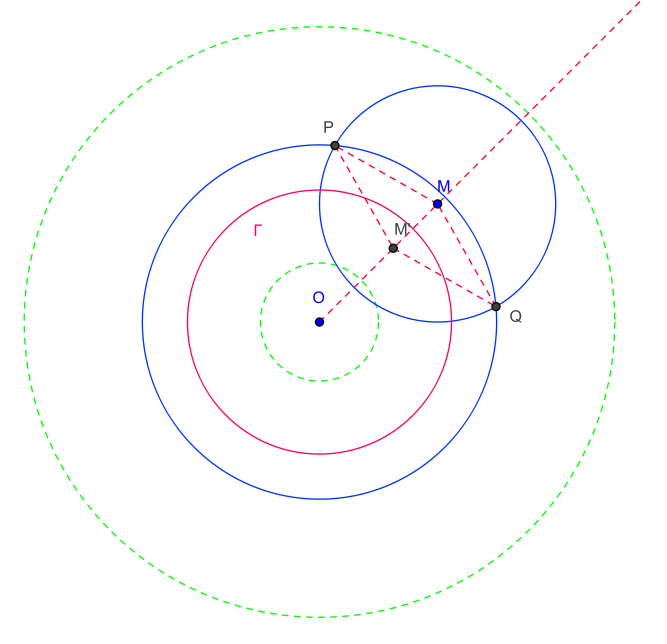
Signalons aussi l’existence de "machines à inversion", l’inverseur de Charles Peaucellier :

L'inverseur est un objet mécanique avec deux barres OP et OQ de longueur fixe et 4 autres barres MP, MQ, M'P, M'Q de longueurs fixes avec les points de pivots aux sommets du losange OMPQM'.

Pour un point du plan affine euclidien et un rapport , avec , on peut construire l’inverse géométrique, pour l’inversion de centre et de rapport , de tout point dans la couronne centrée en , de rayon intérieur , et de rayon extérieur de la façon suivante :

• Un point dans la couronne étant donnée, il existe deux points d’intersection et du cercle de centre et de rayon , et du cercle de centre et de rayon
• Puis on construit l’unique point tel que soit un losange.
• L’application qui à fait correspondre est bien l’inversion cherchée.

Remarque : cet inverseur fut utilisé pour transformer un mouvement rectiligne en mouvement circulaire.
Voir : figure interactive de ChronoMath

Dans le plan complexe

Dans le plan complexe, une inversion particulière est celle par rapport au cercle unité ; en termes d’affixe complexe, elle est codée par l'application . On voit ainsi que cette inversion est composée de la conjugaison complexe et d’une homographie.

C’est en fait un résultat général : un cercle d’inversion étant donné, on choisit trois points sur ce cercle, puis l’unique homographie qui envoie respectivement sur . On vérifie alors que l’application , où dénote la conjugaison complexe, est précisément l’inversion cherchée, et son écriture comme composée d’une homographie et de la conjugaison complexe découle de l’écriture de et comme homographie.

On fait ensuite le lien avec le groupe circulaire, qui est l’ensemble des transformations, définies en fait sur la droite projective complexe, et qui envoient les droites et les cercles sur des droites et des cercles ; en identifiant la droite projective complexe à la sphère de Riemann, cette propriété de conservation s’exprime plus simplement : ce sont les cercles tracés sur cette sphère qui sont conservés. Il est clair que les inversions appartiennent au groupe circulaire ; et relativement simple de montrer qu’il en est de même pour les homographies. On peut montrer ensuite qu’en fait, le groupe circulaire est engendré par inversions et homographies.

Voir aussi

Liens externes

• Inversion et ses propriétés sur Math Web, avec la démonstration du théorème des 7 cercles, du théorème de Ptolémée et de l'inverseur de Hart

• Inversion sur BibM@th
• Inversion de Cercles avec GeoGebra
• (fr) Inversion: une permutation linéaire des cycles (droites et cercles) notes pour lycéens (étudiants du secondaire), par Xavier Hubaut
• (fr) Inversion: transformation conforme notes pour lycéens (étudiants du secondaire), par Xavier Hubaut

Bibliographie

• Michèle Audin, Geometry, Universitext, Springer, ISBN 978-3540434986
• Marcel Berger, Géométrie [détail des éditions] (Tome 1)
• Jean-Denis Eiden, Géométrie analytique classique, Calvage & Mounet, 2009, ISBN 978-2-91-635208-4
• Petite encyclopédie de mathématique (Ed. Didier)
• Méthodes modernes en géométrie de Jean Fresnel
• D. Lehmann et R. Bkouche, Initiation à la géométrie, PUF 1988, ISBN 2 13 040160 0

• Portail de la géométrie