Portance (mécanique des fluides)

« Portance » redirige ici. Pour les autres significations, voir Portance (homonymie).

La portance est la composante de la force subie par un corps en mouvement dans un fluide qui s'exerce perpendiculairement à la direction du mouvement.

Description

Un corps placé dans un écoulement d'air (ou d'eau) subit une force aérodynamique (ou hydrodynamique). Pour l'analyse, on décompose cette force en une composante selon la direction du vent relatif, la traînée (voir aussi Aérodynamique), et une composante perpendiculaire : la portance.

Pour une voile, la portance est dirigée de l'intrados (la face "au vent", creusée), vers l'extrados (la face "sous le vent", bombée).

Pour une aile d'avion, la portance est dirigée de l'intrados (la face inférieure), vers l'extrados (la face supérieure). Les surfaces verticales peuvent développer des portances latérales.

Origine de la portance d'une aile

Généralités

En raison de la différence de pressions au-dessus et au-dessous (différence des vitesses des filets d´air) , l'aile subit une force de réaction vers le haut, c'est la portance.

En subsonique la portance d'une aile de grand allongement est proportionnelle à la circulation de l'air autour de celle-ci (voir Théorème de Kutta-Jukowski). C'est la condition de Kutta qui impose la valeur de la circulation telle qu'il n'y ait pas de vitesse infinie au bord de fuite.

Pour une incidence positive (bord d'attaque au-dessus du bord de fuite), cette circulation crée des vitesses plus élevées sur l'extrados et plus faibles sur l'intrados. Selon le théorème de Bernoulli cela se traduit par des pressions plus fortes sur l'intrados que sur l'extrados donc une portance dirigée vers le haut.

Cette force de portance est générée par l'air qui est expulsé vers le bas, en raison de la forme de l'aile et de l'angle d'incidence. Pour un profil dissymétrique, la forme bombée de l'aile sur sa face supérieure tend à dévier l'écoulement de l'air vers le bas, selon l'effet Coanda.

Par réaction l'aile est tirée vers la haut, en vertu de la troisième loi de Newton^[1]:

« Tout corps A (l'aile) exerçant une force sur un corps B (l'air) subit une force d'intensité égale, de même direction mais de sens opposé, exercée par le corps B ».

Formulation

La portance verticale en Newton (N) d'une aile vaut :

avec

•  : masse volumique du fluide
• S, : surface de référence en m²
• V, : vitesse en m/s
• = coefficient de portance (Nombre sans dimension)

Cette formule, issue de l'analyse dimensionnelle et identique à celle de la traînée, est valable dans tout système d'unités cohérent. Il faut noter qu'elle ne dit pas que la portance est proportionnelle au carré de la vitesse. Seuls des essais peuvent le confirmer, ou l'infirmer, dans un cas particulier. Elle définit un cadre cohérent pour exprimer les résultats de ces essais, le coefficient sans dimensions étant défini comme une fonction d'autres nombres sans dimensions.

Outre des nombres sans dimensions, plus ou moins nombreux, qui expriment la similitude géométrique, interviennent des nombres sans dimensions qui expriment la similitude physique. Le nombre le plus utile pour la portance est le nombre de Mach qui caractérise les effets de la compressibilité. Le nombre de Reynolds qui exprime les effets de la viscosité joue un rôle beaucoup moins important que pour la traînée.

On note parfois où q est la pression dynamique :

• Pour une portance latérale on aurait Fy et Cy à la place de Fz et Cz.
• Dans le cas de la traînée on a Fx et Cx à la place de Fz et Cz.

Détermination du coefficient de portance

Pour un fluide répondant à l'approximation des milieux continus, c'est-à-dire dans lequel on considère des particules fluides de taille supérieure à celle des molécules mais assez petites pour permettre l'utilisation des différentielles, les équations générales de la mécanique des fluides sont les équations de Navier-Stokes. Dans les problèmes liés à la portance d'un profil mince, la viscosité et la turbulence sont généralement négligeables ; le fluide est donc considéré comme parfait soumis aux équations d'Euler nettement plus simples.

Celles-ci se traitent en général par la théorie des écoulements à potentiel de vitesse et, plus particulièrement, par la théorie des profils minces.

Variables affectant la portance

Cette formule met en jeu les paramètres suivants :

• La masse volumique ρ du fluide. L'eau a une masse volumique environ mille fois plus grande que l'air. Toutes choses égales par ailleurs elle exerce donc une poussée mille fois plus grande. Pour une vitesse 10 fois plus faible, la portance d'une aile immergée ou foil est encore 10 fois plus forte que celle d'une aile d'avion. Un m² d'aile d'avion de ligne porte 600 à 700 kg; un m² de foil peut porter 6 à 10 tonnes. Cela explique que quelques m² de foils suffisent à faire voler un hydroptère d'une masse de l'ordre de la dizaine de tonnes.
• La surface S de l'aile (surface alaire). Le déploiement vers l'arrière des volets d'une aile à basse vitesse (atterrissage et décollage) peut augmenter la surface effective de l'aile, cependant par convention la valeur S reste la même, c'est le coefficient de portance qui augmente.
• Le carré de la vitesse V. « La portance est une fleur qui naît de la vitesse » (Capitaine Ferber, pionnier de l'aviation).
• Le coefficient de portance de l'aile ou de la voile qui dépend :
  • de l'angle d'incidence, en anglais : angle d'attaque, et de la pente de portance de l'aile, fonction de son allongement. Lorsque l'angle augmente la portance augmente jusqu'à l'angle de portance maximale qui dépend du profil de l'aile ^[2]. Une fois cet angle dépassé, la portance s'effondre, c'est le décrochage
  • de la forme en plan de l'aile et de sa flèche,
  • du profil de l'aile, notamment de sa cambrure,
  • de la modification de ce profil (corde et cambrure) par des dispositifs hypersustentateurs, becs et volets de courbure (slats/flaps en anglais), utilisés au décollage et à l'atterrissage,
  • de l'effet du Nombre de Reynolds et du Nombre de Mach sur la pente de portance et sur l'incidence de décrochage,
  • de la génération de tourbillons porteurs à grande incidence (aile delta),
  • de la proximité du sol : l'effet de sol en diminuant la déflexion augmente l'incidence locale donc la portance.
  • de la cavitation générée sur la surface de l'aile lorsqu'elle est placée dans un milieu liquide avec une vitesse assez grande.

Influence du Reynolds et de la compressibilité

L'intérêt de cette formulation réside dans le fait que les coefficients aérodynamiques dont le C_z peuvent être considéré comme constants, dans une configuration et à une incidence données. Cependant ce n'est pas tout à fait le cas, il varie selon le nombre de Reynolds et le nombre de Mach :

• Nombre de Reynolds : il dépend de la viscosité de l'air (qui varie selon la température), de la corde de l'aile et de la vitesse. La portance, sauf la portance maximale (l'incidence de décrochage), et contrairement à la traînée, en dépend peu. Ainsi, le C_z est pratiquement constant. La portance pourrait donc exister en fluide parfait (air non visqueux) alors que la traînée serait nulle. Néanmoins la viscosité joue un rôle dans l'origine de la portance comme expliqué ci-dessous.

• Compressibilité : quand l'avion va à une vitesse faible par rapport à celle du son, le fluide peut être considéré comme incompressible. La portance est alors proportionnelle au carré de la vitesse. Au-delà de Mach 0,3 environ, en subsonique, il faut apporter au C_z une correction fonction du nombre de Mach. En supersonique, pour les avions capables de franchir le mur du son, il se produit des ondes de choc, au travers desquelles l'écoulement diminue brutalement de vitesse, le C_z est alors principalement déterminé par le Mach. Autour de la vitesse du son (le transsonique), l'écoulement transsonique est beaucoup plus complexe car l'emplacement des ondes de choc évolue rapidement, et le C_z est variable.

Effet Magnus

Considérons un cylindre à section circulaire de longueur supposée infinie fixé en travers d'un écoulement de vitesse U supposée de gauche à droite : il subit en général une traînée dans la direction de l'écoulement qui peut avoir plusieurs origines selon les circonstances, mais pas de portance perpendiculaire à l'écoulement (sauf dans le cas de tourbillons dissymétriques ou alternés).

Si le cylindre est soumis à une rotation autour de son axe, le fluide visqueux situé en contact avec est entraîné (condition de non-glissement). Cela se traduit dans chaque section droite par une circulation , intégrale des vitesses fluides sur son périmètre. Si le cylindre tourne dans le sens rétrograde, l'écoulement est déformé de telle manière que la vitesse au point le plus haut s'ajoute à la vitesse en l'absence de rotation tandis qu'elle se retranche au point le plus bas. Ainsi, selon le théorème de Bernoulli appliqué ici, comme il se doit, au cas d'un fluide supposé incompressible, il y a des surpressions sur la partie inférieure et des dépressions sur la partie supérieure. On montre en mécanique des fluides que la portance ainsi créée est perpendiculaire à la vitesse de l'écoulement et vaut par unité de longueur du cylindre, ρ étant la masse volumique du fluide :

Ce résultat est connu sous le nom de théorème de Kutta-Joukowsky.

Écoulement autour d'un cercle.

Portance d'une aile d'envergure infinie

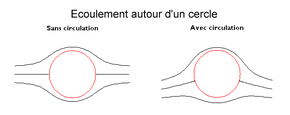
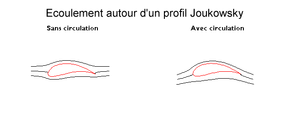
Par une transformation conforme (qui conserve les angles), on peut transformer le cylindre à section circulaire en une aile de profil constant. Le théorème précédent est toujours valable mais le problème physique concerne l'origine de la circulation. En effet, il est hors de question de faire tourner l'aile pour obtenir un effet Magnus.

Pour comprendre alors la création de circulation à l'origine de la portance il faut remarquer que, sur le profil comme sur le cercle considéré précédemment, l'écoulement présente deux points d'arrêt. En l'absence de circulation, le point d'arrêt amont se trouve au voisinage du bord d'attaque tandis que le point d'arrêt aval se trouve au voisinage du bord de fuite sur l'extrados. Il en résulte que le filet fluide qui a longé l'intrados devrait pivoter brutalement au bord de fuite pour retrouver ce point d'arrêt aval, ce qui conduirait à des vitesses infinies et n'est pas conforme à l'expérience. Il se crée alors une circulation qui pousse ce point d'arrêt jusqu'au bord de fuite : c'est la condition de Kutta qui assure un équilibre stable de l'écoulement en fixant la circulation de manière unique.

En utilisant l'aile comme référence pour les vitesses, on voit que l'écoulement se fait dans le sens bord d'attaque, extrados, bord de fuite, intrados. En fait, la circulation est conservée par la création d'un tourbillon de sens inverse qui est «déversé» dans le sillage et s'éloigne vers l'aval avant de disparaître sous l'effet des frottements visqueux.

On ne modifie pas la portance si on remplace le profil par un simple tourbillon, l'aile apparaissant comme une ligne de tourbillons liés. On peut également associer cette portance à l'écoulement qui se dirige vers le haut à l'amont et vers le bas à l'aval.

La portance est décrite par une formule analogue à celle indiquée pour l'effet Magnus. La circulation était alors proportionnelle à la vitesse de rotation imposée au cylindre. Ici, la condition de Joukowsky crée une circulation proportionnelle à la vitesse relative loin de l'aile. La portance est alors proportionnelle au carré de la vitesse et il est donc possible de mettre l'expression sous la forme classique indiquée dans Formulation, sans que la pression dynamique intervienne en quoi que ce soit dans cette force perpendiculaire à la direction générale de l'écoulement.

Écoulement autour d'un profil Joukowsky.

Portance d'une aile d'envergure finie

Exemple de traînées de condensation

Mise en évidence de la turbulence de sillage induite par le tourbillon marginal

Pour une aile d'envergure finie, la ligne de tourbillons décrite précédemment ne peut s'arrêter brusquement en bout d'aile. En fait, la surpression de l'intrados par rapport à l'extrados conduit à une égalisation en bout d'aile à travers un écoulement transversal des hautes pressions vers les basses pressions, soit vers l'extérieur sur l'intrados et vers l'intérieur sur l'extrados.

Ces mouvements amorcent des tourbillons qui se développent vers l'aval, d'intensité décroissante à mesure qu'on s'éloigne des extrémités de l'aile. À quelque distance du bord de fuite, ce système tourbillonnaire se réduit à deux lignes de tourbillons d'extrémités d'aile. L'ensemble de ces deux lignes et de la ligne de tourbillons liés à l'aile forme le système de tourbillons en fer à cheval.

Dans une atmosphère humide, la détente qui est à l'origine de ces tourbillons peut amener l'air à se saturer. La condensation éphémère qui en résulte peut parfois mettre en évidence les tourbillons partant des extrémités de l'aile (traînée de condensation dite fugace). Une condition propice à la formation de telles trainées est une forte incidence, que l'on rencontre lors d'évolutions sérées (voltige ou vols de démonstration) ou à basse vitesse (phase d'atterrissage d'un avion par exemple).

Traînée d'une aile portante

La portance crée derrière l'aile une déflexion de l'air vers le bas (en anglais : downwash) . La création de ce mouvement consomme de l'énergie, ce qui se traduit par une traînée induite (par la portance). C'est le prix à payer pour que les avions volent.

Aux extrémités de l'aile la discontinuité entre cette déflexion et l'air non perturbé — des deux côtés de l'aile — est à l'origine des tourbillons marginaux^[3].

À cette traînée liée à la portance, il convient d'ajouter la traînée de frottement liée à la viscosité dans la couche limite.

Mesure de la portance

La portance peut être mesurée grâce à l'expérience de la butée Michell.

Notes et références

Voir aussi

Liens internes

• Stabilité longitudinale (aviation)

Liens externes

• NASA What is lift
• Applied Aerodynamics

• Portail de l’aéronautique