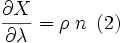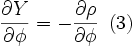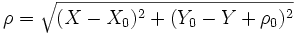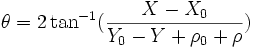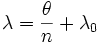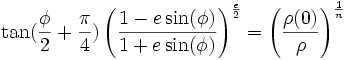Projection de Lambert

Projection de Lambert

Projection conique conforme de Lambert

Page d'aide sur l'homonymie Pour les articles homonymes, voir Lambert.
Page d'aide sur l'homonymie Ne doit pas être confondu avec Projection azimutale équivalente de Lambert.

La projection conique conforme de Lambert, ou plus simplement, la projection de Lambert est l'une des projections cartographiques présentées par le mathématicien mulhousien Johann Heinrich Lambert en 1772[1].

Dans ce système de projection conforme, les méridiens sont des droites concourantes, et les parallèles des arcs de cercle centrés sur le point de convergence des méridiens.

Le système a été adopté par l'artillerie française au cours de la première guerre mondiale pour les cartes à grande échelle (1/20 000 et au-dessus), une carte conforme étant nécessaire pour la préparation des tirs, ce que ne permettait pas la projection de Bonne alors en usage.

Elle est depuis cette époque la projection officielle utilisée pour représenter la France métropolitaine, avec différents paramètres successifs suivant les époques. C'est aussi la projection officielle en Belgique et en Estonie, ainsi que pour les cartes couvrant toute l'Europe à des échelles inférieures ou égales au 1:500 000[2].

Sommaire

Définition

Projection conique.jpg

Cette projection est une projection conique conforme (qui conserve les angles).

Le sommet du cône appartient à l'axe des pôles et est tangent à un ellipsoïde de référence en un point défini par un méridien de référence et un parallèle de référence de latitude φ0 qui est aussi l'angle au sommet du cône. Le cône peut également être sécant à l'ellipsoïde au niveau de deux parallèles, dits alors parallèles automécoïques φ1 et φ2. La définition d'une projection de Lambert peut ainsi se faire soit par un parallèle tangent et un facteur d'échelle, soit par deux parallèles sécants et isométriques.

Le cône est ensuite développé sur un plan, sans déformation.

Dans cette projection on retrouve :

  • les parallèles (latitude constante) sont des cercles concentriques autour du point P, projection du pôle Nord et sommet du cône.
  • les méridiens (longitude constante) sont des droites concourantes en P.
  • l'axe des ordonnées est la projection du méridien de référence.
  • l'origine se trouve au point de référence.
  • le cercle, projection du point de référence, est appelé isomètre ou isomètre de référence. En effet, c'est selon ce cercle que l'on définit l'échelle de la carte.
  • les angles sont conservés.

La déformation linéaire est relativement importante lorsque l'on s'éloigne du parallèle d'origine, il est donc courant de définir des zones différant par leur angle φ0.

Enfin cette projection étant utilisée en cartographie, pour éviter d'avoir des abscisses et des ordonnées négatives, on effectue une translation en affectant des coordonnées positives au point de référence.

Projections officielles en France métropolitaine

La projection Lambert93 (projection officielle pour les cartes de France métropolitaine depuis le décret du 26 décembre 2000) est la projection liée au système géodésique RGF93. Elle utilise deux parallèles sécants : 44°N et 49°N, le méridien de référence 3°E (Greenwich), le parallèle d'origine (qui n'est pas de référence puisqu'on utilise des parallèles sécants) 46°30', et les coordonnées d'origine (700 000 m, 6 600 000 m).

Son principal intérêt réside dans son référentiel RGF93, qui est d'une part commun aux voisins européens de la France car fondé sur ETRS89, et d'autre part compatible avec le WGS84 utilisé notamment par le système GPS de positionnement par satellite (le passage de RGF93 à WGS84 se fait par une translation métrique, et des rotations et mises à l'échelle de l'ordre de 10-9, les rendant virtuellement identiques pour la plupart des applications pratiques). Ces trois systèmes ont de plus en commun l'ellipsoïde de référence IAG GRS80.

Définition précise de la projection officielle Lambert93 par l'IGN

En pratique, cette projection est encore peu utilisée, en partie du fait des altérations linéaires importantes qui y sont associées (2,3 m/km à Dunkerque, 0,60 m/km à Marseille et 2,95 m/km à Bonifacio, légèrement inférieures à celles de la projection Lambert 2 étendue). Pour y remédier, le décret 2006-272 entérine la création de 9 projections coniques conformes sécantes, couvrant 9 zones du nord au sud, telles que proposées par un rapport du CNIG. Elles ont en commun avec le Lambert93 le système géodésique RGF93 et le méridien de référence 3°E (Greenwich).

Projection φ0 φ1 φ2 X0 Y0
CC42 42° 41.25° 42.75° 1 700 000 m 1 200 000 m
CC43 43° 42.25° 43.75° 1 700 000 m 2 200 000 m
CC44 44° 43.25° 44.75° 1 700 000 m 3 200 000 m
CC45 45° 44.25° 45.75° 1 700 000 m 4 200 000 m
CC46 46° 45.25° 46.75° 1 700 000 m 5 200 000 m
CC47 47° 46.25° 47.75° 1 700 000 m 6 200 000 m
CC48 48° 47.25° 48.75° 1 700 000 m 7 200 000 m
CC49 49° 48.25° 49.75° 1 700 000 m 8 200 000 m
CC50 50° 49.25° 50.75° 1 700 000 m 9 200 000 m

Icône pour souligner l'importance du texte Dans l'attente d'une définition officielle de ces projections, les Y0 ci-dessus sont donnés sous toutes réserves et selon cette publication du CERTU, des valeurs de 42 200 000 m à 50 200 000 m ayant également été publiées!

Dans les faits, les projections dites Lambert 4 Zones définies en 1920, associées au système NTF (Nouvelle triangulation de la France), restent encore utilisées.

Leur ellipsoïde de référence est l'ellipsoïde de Clarke 1880 IGN, et leur méridien de référence le méridien de Paris (qui passe au milieu de la façade de l'Observatoire de Paris, soit 2°20´14.025" Est du méridien de Greenwich). Les coordonnées angulaires associées au système NTF sont exprimées en grades (gon) et non en degrés, pour profiter de l'équivalence 1 grade de latitude = 100 km. La France est ainsi découpée en quatre zones qui s'étendent à 150 km au sud et au nord de chaque parallèle d'origine, sauf au nord de la zone 1 (200 km), et au sud de la zone 3 (200 km).

A cela s'ajoute la projection Lambert Grand Champ (très peu utilisée, citée pour mémoire), qui elle se définit avec des coordonnées angulaires en degrés.

Projection φ0 φ1 φ2 Translation X Translation Y
Lambert I (Nord) 55 grades 48°35’54,682” 50°23’45,282” 600 000 m 200 000 m
Lambert II (Centre) 52 grades 45°53’56,108” 47°41’45,652” 600 000 m 200 000 m
Lambert III (Sud) 49 grades 43°11’57,449” 44°59’45,938” 600 000 m 200 000 m
Lambert IV (Corse) 46,85 grades 41°33’37,396” 42°46’03,588” 234,358 m 185 861,369 m
Lambert I Carto (Nord) 55 grades 48°35’54,682” 50°23’45,282” 600 000 m 1 200 000 m
Lambert II Carto (Centre) 52 grades 45°53’56,108” 47°41’45,652” 600 000 m 2 200 000 m
Lambert III Carto (Sud) 49 grades 43°11’57,449” 44°59’45,938” 600 000 m 3 200 000 m
Lambert IV Carto (Corse) 46,85 grades 41°33’37,396” 42°46’03,588” 234,358 m 4 185 861,369 m
Lambert Grand Champ 47° 45° 49° 600 000 m 600 000 m

On signalera que avec les coordonnées Lambert, Le Lambert Zone "Carto" est utilisé par l'IGN depuis 1972, alors que le Lambert zone "standard" reste utilisé par les services du Cadastre ou autres utilisateurs locaux (géomètres notamment) : ainsi, en Lambert 3, on pourra trouver Y=3 256 315 sur les cartes IGN et Y=256 315 au cadastre. Cette notation dite "standard" est une survivance d'anciennes définitions IGN, et ne devrait plus être utilisée depuis 1972.

Pour les représentations devant couvrir la France entière en une projection, la projection utilisée est la "Lambert 2 étendue", qui reprend tous les paramètres de la Lambert 2 Carto. C'est à ce jour la projection généralement utilisée dans les SIG français. À terme la projection Lambert93 remplacera le lambert 2 étendu, qui ne présente plus de compatibilité et de précision suffisantes.

Formules mathématiques

Pour l'application numérique, on rappelle ici les paramètres pour la projection Lambert 93 :

  • a = 6 378 137 m
  • b = a.(1 - f)
  • f = 1 / 298.257222101
  • φ0 = 46°30
  • φ1 = 44°
  • φ2 = 49°
  • λ0 = 3°
  • X0 = 700 000 m
  • Y0 = 6 600 000 m

Des coordonnées géographiques (lat, lon) aux cartographiques (X, Y)

Partant d'un point (φ, λ) du globe supposé être une ellipsoïde de demi-grand axe a et de demi-petit axe b, calculons ses coordonnées (X, Y) sur la carte. Pour cela, nous allons passer par les coordonnées (ρ, θ) du point projeté sur le cône. L'axe des X est croissant vers l'Est et l'axe des Y croissant vers le Nord.

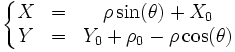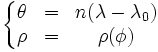\left\{\begin{matrix} X& = &\rho \sin(\theta) + X_0\\ Y& =& Y_0 + \rho_0 - \rho \cos(\theta)\end{matrix}\right. où \left\{\begin{matrix}\theta & =& n(\lambda - \lambda_0)\\\rho & = &\rho(\phi)\end{matrix}\right.


Démonstration

Puisque c'est une projection conforme pour un point M à la surface de la terre :

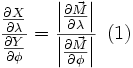
\frac{ \frac{\partial X}{\partial\lambda}}{\frac{\partial Y}{\partial\phi}} = \frac{\left| \frac{\partial \vec M}{\partial \lambda} \right|}{\left| \frac{\partial \vec M}{\partial \phi} \right|}\ \left(1\right)

On peut donc calculer ρ le long du méridien d'origine (λ = λ0)

  • \frac{\partial X}{\partial \lambda} = \rho\;n\ \left(2\right)
  • \frac{\partial Y}{\partial \phi} = - \frac{\partial \rho}{\partial \phi}\ \left(3\right)

Le méridien est une ellipse d'équation :

\left\{\begin{matrix} r & = a\cos(t) \\ z & = b\sin(t)\end{matrix}\right.\forall t \in [0;2\pi]

La latitude étant l'angle que fait le méridien du lieu avec le plan équatorial, on trouve :

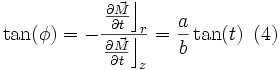
\tan(\phi) = -\frac{\left.\frac{\partial \vec M}{\partial t} \right\rfloor_r}{\left.\frac{\partial \vec M}{\partial t} \right\rfloor_z} = \frac{a}{b}\tan(t)\ \left(4\right)

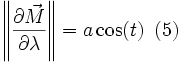
\left\|\frac{\partial \vec M}{\partial \lambda}\right\| = a\cos(t)\ \left(5\right)

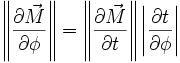
\left\|\frac{\partial \vec M}{\partial \phi}\right\| = \left\|\frac{\partial \vec M}{\partial t}\right\| \left|\frac{\partial t}{\partial \phi}\right|

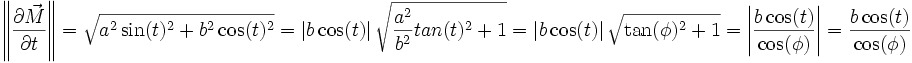
\left\|\frac{\partial \vec M}{\partial t}\right\| = \sqrt{a^2 \sin(t)^2 + b^2 \cos(t)^2} = \left|b\cos(t)\right|\sqrt{ \frac{a^2}{b^2}tan(t)^2 + 1} = \left|b\cos(t)\right|\sqrt{\tan(\phi)^2 + 1} = \left|\frac{b\cos(t)}{\cos(\phi)}\right| = \frac{b\cos(t)}{\cos(\phi)}

On peut dériver (4) par rapport à φ :

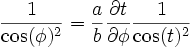
\frac{1}{\cos(\phi)^2} = \frac{a}{b}\frac{\partial t}{\partial \phi}\frac{1}{\cos(t)^2}

Ce qui donne en regroupant les trois dernières équations :

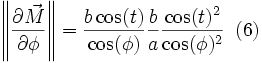
\left\|\frac{\partial \vec M}{\partial \phi}\right\| = \frac{b\cos(t)}{\cos(\phi)}\frac{b}{a}\frac{\cos(t)^2}{\cos(\phi)^2}\ \left(6\right)

Et en regroupant (1), (2), (3), (5) et (6) :

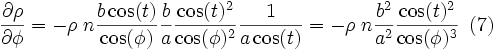
\frac{\partial \rho}{\partial \phi} = - \rho\;n \frac{b\cos(t)}{\cos(\phi)}\frac{b}{a}\frac{\cos(t)^2}{\cos(\phi)^2} \frac{1}{a\cos(t)} = -\rho\;n\frac{b^2}{a^2}\frac{\cos(t)^2}{\cos(\phi)^3}\ \left(7\right)

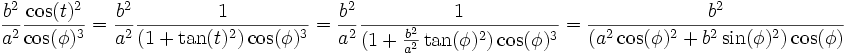
\frac{b^2}{a^2}\frac{\cos(t)^2}{\cos(\phi)^3} = \frac{b^2}{a^2}\frac{1}{(1 + \tan(t)^2)\cos(\phi)^3} = \frac{b^2}{a^2}\frac{1}{(1 + \frac{b^2}{a^2}\tan(\phi)^2)\cos(\phi)^3} = \frac{b^2}{(a^2\cos(\phi)^2 + b^2\sin(\phi)^2)\cos(\phi)}\,

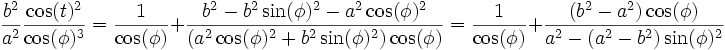
\frac{b^2}{a^2}\frac{\cos(t)^2}{\cos(\phi)^3} = \frac{1}{\cos(\phi)} + \frac{b^2 - b^2\sin(\phi)^2 - a^2\cos(\phi)^2}{(a^2\cos(\phi)^2 + b^2\sin(\phi)^2)\cos(\phi)} = \frac{1}{\cos(\phi)} + \frac{(b^2-a^2)\cos(\phi)}{a^2 - (a^2 - b^2)\sin(\phi)^2}\,

Or e\,, l'excentricité d'une ellipse vérifie : 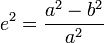e^2 = \frac{a^2 - b^2}{a^2}. Ce qui nous donne :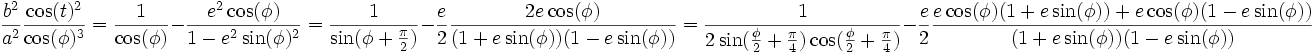

\frac{b^2}{a^2}\frac{\cos(t)^2}{\cos(\phi)^3} = \frac{1}{\cos(\phi)} - \frac{e^2\cos(\phi)}{1 - e^2\sin(\phi)^2} = \frac{1}{\sin(\phi + \frac{\pi}{2})} - \frac{e}{2}\frac{2e\cos(\phi)}{(1 + e\sin(\phi))(1 - e\sin(\phi))} = \frac{1}{2\sin(\frac{\phi}{2} + \frac{\pi}{4})\cos(\frac{\phi}{2} + \frac{\pi}{4})} - \frac{e}{2}\frac{e\cos(\phi)(1 + e\sin(\phi)) + e\cos(\phi)(1 - e\sin(\phi))}{(1 + e\sin(\phi))(1 - e\sin(\phi))}

Et finalement en utilisant les dérivées de la fonction \ln\, :

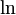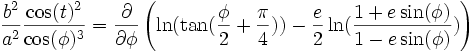
\frac{b^2}{a^2}\frac{\cos(t)^2}{\cos(\phi)^3} = \frac{\partial}{\partial \phi}\left(\ln(\tan(\frac{\phi}{2} + \frac{\pi}{4})) - \frac{e}{2}\ln(\frac{1 + e\sin(\phi)}{1 - e\sin(\phi)})\right)

On peut donc réécrire l'équation (7) en :

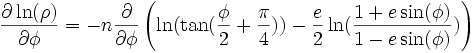
\frac{\partial \ln(\rho)}{\partial \phi} = -n\frac{\partial}{\partial \phi}\left(\ln(\tan(\frac{\phi}{2} + \frac{\pi}{4})) - \frac{e}{2}\ln(\frac{1 + e\sin(\phi)}{1 - e\sin(\phi)})\right)

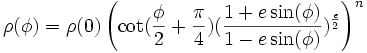
\rho(\phi) = \rho(0)\left(\cot(\frac{\phi}{2} + \frac{\pi}{4})(\frac{1 + e\sin(\phi)}{1 - e\sin(\phi)})^{\frac{e}{2}}\right)^n

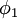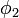Nous allons travailler ici avec deux parallèles sécants de référence. Sur ces parallèles, appelés automécoïques, de latitude \phi_1\, et \phi_2\,, l'échelle est conservée : 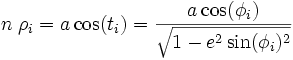n\;\rho_i = a\cos(t_i) = \frac{a\cos(\phi_i)}{\sqrt{1 - e^2\sin(\phi_i)^2}}\, On peut donc calculer n et ρ(0) :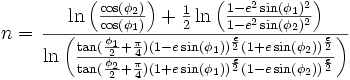

n = \left.\frac{\ln\left(\frac{\cos(\phi_2)}{\cos(\phi_1)}\right)+\frac{1}{2}\ln\left(\frac{1-e^2\sin(\phi_1)^2}{1-e^2\sin(\phi_2)^2}\right)}{\ln\left(\frac{\tan(\frac{\phi_1}{2}+\frac{\pi}{4})(1 - e\sin(\phi_1))^{\frac{e}{2}}(1 + e\sin(\phi_2))^{\frac{e}{2}} }{\tan(\frac{\phi_2}{2}+\frac{\pi}{4})(1 + e\sin(\phi_1))^{\frac{e}{2}}(1 - e\sin(\phi_2))^{\frac{e}{2}} }\right)}\right.

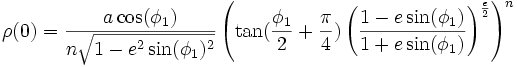
\rho(0) = \frac{a\cos(\phi_1)}{n\sqrt{1 - e^2\sin(\phi_1)^2}}\left(\tan(\frac{\phi_1}{2} + \frac{\pi}{4})\left(\frac{1-e\sin(\phi_1)}{1+e\sin(\phi_1)}\right)^{\frac{e}{2}}\right)^n

Des coordonnées cartographiques (X,Y) aux géographiques (lat, lon)

De même que ci-dessus nous allons passer par les coordonnées (ρ, θ) du point projeté sur le cone :

  • \rho = \sqrt{(X - X_0)^2 + (Y_0 - Y + \rho_0)^2}
  • \theta = 2\tan^{-1}(\frac{X - X_0}{Y_0 - Y + \rho_0 + \rho})

Comme on a vu plus haut, on a alors :

  • \lambda = \frac{\theta}{n} + \lambda_0\,
  • \tan(\frac{\phi}{2} + \frac{\pi}{4})\left(\frac{1 - e\sin(\phi)}{1 + e\sin(\phi)}\right)^{\frac{e}{2}} = \left(\frac{\rho(0)}{\rho}\right)^\frac{1}{n}

Si on appelle F la fonction de gauche, puisque F est strictement décroissante :

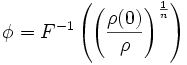
\phi = F^{-1}\left(\left(\frac{\rho(0)}{\rho}\right)^\frac{1}{n}\right)

Mais le calcul de F − 1 n'est pas trivial. Pour calculer φ avec une précision arbitraire, puisque F est continue sur son intervalle de définition, on peut utiliser un algorithme dichotomique. On peut aussi, pour plus de rapidité, utiliser l'algorithme proposé par l'IGN :

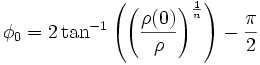
  • \phi_0 = 2\tan^{-1}\left(\left(\frac{\rho(0)}{\rho}\right)^\frac{1}{n}\right) - \frac{\pi}{2}
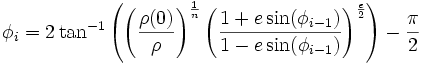
  • \phi_i = 2\tan^{-1}\left(\left(\frac{\rho(0)}{\rho}\right)^\frac{1}{n}\left(\frac{1 + e\sin(\phi_{i-1})}{1 - e\sin(\phi_{i-1})}\right)^\frac{e}{2}\right) - \frac{\pi}{2}
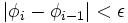
  • jusqu'à ce que \left|\phi_i - \phi_{i-1}\right| < \epsilon

Bibliographie

  1. ↑ Karen Mulcahy, « Cylindrical Projections », City University of New York. Consulté le 30 mars 2007
  2. ↑ (en) [pdf] Institute for Environment and Sustainability, European Communities,Map Projections for Europe, 2001, page 43.

Voir aussi

Ce document provient de « Projection conique conforme de Lambert ».

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Projection de Lambert de Wikipédia en français (auteurs)

Игры ⚽ Нужен реферат?

Regardez d'autres dictionnaires:

  • Projection de lambert — Projection conique conforme de Lambert Pour les articles homonymes, voir Lambert.  Ne doit pas être confondu avec Projection azimutale équivalente de Lambert. La projection conique conforme de Lambert, ou plus simplement, la projection de… …   Wikipédia en Français

  • Lambert-93 — Projection conique conforme de Lambert Pour les articles homonymes, voir Lambert.  Ne doit pas être confondu avec Projection azimutale équivalente de Lambert. La projection conique conforme de Lambert, ou plus simplement, la projection de… …   Wikipédia en Français

  • Lambert 93 — Projection conique conforme de Lambert Pour les articles homonymes, voir Lambert.  Ne doit pas être confondu avec Projection azimutale équivalente de Lambert. La projection conique conforme de Lambert, ou plus simplement, la projection de… …   Wikipédia en Français

  • Projection azimuthale équivalente de Lambert — Projection azimutale équivalente de Lambert  Ne doit pas être confondu avec Projection conique conforme de Lambert. La projection azimutale équivalente d …   Wikipédia en Français

  • Lambert (conformal conic) projection — or Lambert projection [lam′bərt] n. 〚see LAMBERT〛 a map projection in which all meridians are represented by straight lines radiating from a common point outside the mapped area and the parallels are represented by arcs or circles whose center is …   Universalium

  • Lambert (conformal conic) projection — or Lambert projection [lam′bərt] n. [see LAMBERT] a map projection in which all meridians are represented by straight lines radiating from a common point outside the mapped area and the parallels are represented by arcs or circles whose center is …   English World dictionary

  • Lambert (conformal conic) projection — or Lambert projection [lam′bərt] n. [see LAMBERT] a map projection in which all meridians are represented by straight lines radiating from a common point outside the mapped area and the parallels are represented by arcs or circles whose center is …   English World dictionary

  • Lambert projection — Lambert conformal projection or Lambert projection, a map projection in which the meridians are drawn on the surface of a cone and the parallels are spaced mathematically to conform to the actual shape of the features represented. ╂[< Johann H …   Useful english dictionary

  • Projection conique conforme de Lambert — Pour les articles homonymes, voir Lambert.  Ne doit pas être confondu avec Projection azimutale équivalente de Lambert. La pro …   Wikipédia en Français

  • Projection UTM — Transverse Universelle de Mercator La Transverse universelle de Mercator (en anglais Universal Transverse Mercator ou UTM) est un type de projection conforme de la surface de la Terre. L’Allemagne l’utilise sous le nom de Projection de Gauss… …   Wikipédia en Français

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”