Théorème des résidus

Théorème des résidus

Le théorème des résidus en analyse complexe est un outil puissant pour évaluer des intégrales curvilignes de fonctions holomorphes sur des courbes fermées ; il peut aussi bien être utilisé pour calculer des intégrales de fonctions réelles ainsi que la somme de certaines séries. Il généralise le théorème intégral de Cauchy et la formule intégrale de Cauchy.

Sommaire

Énoncé

Soient U un sous-ensemble ouvert et simplement connexe du plan complexe \mathbb C, z1,...,zn un ensemble de points distincts et isolés de U et f une fonction définie et holomorphe sur U \ {z1,...,zn}.

Si γ est une courbe rectifiable dans U qui ne rencontre aucun des points singuliers zk et dont le point de départ correspond au point d'arrivée (c'est-à-dire un lacet rectifiable), alors :

\oint_\gamma f(z) \text{d}z = 2\pi i \sum_{k=1}^n \operatorname{Res}( f, z_k )\,\mathrm{Ind}_\gamma(z_k).

Ici, Res(f,zk) désigne le résidu de f en zk, et Indγ(zk) l'indice du lacet γ par rapport à zk. L'indice de sommation Σ porte sur tous les points singuliers zk, y compris le point à l'infini. Intuitivement, l'indice du lacet est le nombre de tours autour de zk effectués par un point parcourant tout le lacet. Ce nombre de tours est un entier ; il est positif si γ est parcouru dans le sens inverse des aiguilles d'une montre (sens direct) autour de zk, nul si γ ne se déplace pas du tout autour de zk, et négatif si γ est parcouru dans le sens des aiguilles d'une montre autour de zk.

L'indice est défini par

\operatorname{Ind}_\gamma(z_k) = \frac{1}{2\pi i} \int_{\gamma} \frac{\text{d}z}{z-z_k}.
Démonstration

Soit F l'ensemble des points singuliers de la fonction f, soit z_0\in F , la fonction admet un développement de Laurent sur un certain disque épointé D(z_0,r)\backslash\{z_0\} avec r > 0 centré en z0 :

f(z) = \sum_{n\in\mathbb Z} b_{z_0,n} (z-z_0)^n

Soit h_{z_0} la série normalement convergente sur les compacts de U − {z0} définie par la partie singulière du développement de Laurent de f :

h_{z_0}(z) = \sum_{-\infty}^{-1} b_{z_0,n} (z-z_0)^n

Considérons à présent la fonction g holomorphe sur U et définie par

g(z) = f(z) - \sum_{z_i\in F} h_{z_i}(z)

c'est-à-dire la fonction f moins ses développements au voisinage de ses singularités. U étant un ouvert simplement connexe, le lacet γ est homotope à un point dans U et par conséquent,

\oint_\gamma g(z)dz = 0

nous avons donc :

\oint_\gamma f(z) dz = \sum_{z_i\in F} \oint_\gamma h_{z_i}(z) dz

Étant donné que les séries h_{z_i} sont normalement convergentes, on peut écrire :

\oint_\gamma h_{z_i}(z) dz = \sum_{-\infty}^{-1} b_{z_i, n}\oint_\gamma (z-z_i)^n dz

et on a :

\oint_\gamma (z-z_i)^n dz = 2i\pi \mathrm{Ind}_\gamma(z_i) \delta_{n,-1}

où δ est le delta de kronecker. On a utilisé le fait que (z − zi)n possède une primitive holomorphe pour tout n \neq -1 par conséquent l'intégrale ci-dessus est nulle sauf pour n = − 1. Dans ce cas, on retrouve la définition de l'indice. En insérant ce résultat dans la formule précédente, on obtient :

\oint_\gamma f(z)dz = 2i\pi\sum_{z_i\in F} b_{z_i, -1} \mathrm{Ind}_\gamma (z_i)

soit encore par définition du résidu:

\oint_\gamma f(z) dz = 2i\pi\sum_{z_i\in F} \mathrm{Res}(f, z_i)\mathrm{Ind}_\gamma(z_i)

Application au calcul d'intégrales réelles

Pour évaluer des intégrales réelles, le théorème des résidus s'utilise souvent de la façon suivante : l'intégrande est prolongé en une fonction holomorphe sur un ouvert du plan complexe ; ses résidus sont calculés, et une partie de l'axe réel est étendue à une courbe fermée en lui attachant un demi-cercle dans le demi-plan supérieur ou inférieur. L'intégrale suivant cette courbe peut alors être calculée en utilisant le théorème des résidus. Souvent, la partie de l'intégrale sur le demi-cercle tend vers zéro (lemme de Jordan), quand le rayon de ce dernier tend vers l'infini, laissant seulement la partie de l'intégrale sur l'axe réel, celle qui initialement nous intéressait.

La liste ci-dessous n'est pas exhaustive mais elle permet d'avoir une idée générale de la technique utilisant le théorème des résidus, on aborde :

  • Les intégrales du "premier type" : \int_{0}^{2\pi} R(\cos(t),\sin(t))\mathrm{d}t où R est une fonction rationnelle,
  • Les intégrales du "second type" : \int_{-\infty}^{+\infty}f(x)\mathrm{d}x,
  • Les intégrales du "troisième type" : \int_{-\infty}^{+\infty}f(x)\mathrm{e}^{iax}\mathrm{d}x,
  • Les intégrales du "quatrième type" : combinaison des deux cas précédents en considérant la valeur principale de Cauchy de l'intégrale.

Premier type

Soit le calcul de l'intégrale réelle suivante :

I = \int_0^{2\pi} R(\cos(t), \sin(t)) dt

avec R une fonction rationnelle ayant un nombre fini de points singuliers zj n'appartenant pas au cercle C(0,1) centré à l'origine et de rayon 1. On obtient par le théorème des résidus :

I = 2i\pi \sum_{|z_j|<1} \mathrm{Res}(f, z_j)

où f est définie comme suit :

f(z) = \frac{1}{iz} R\left(\frac{z+z^{-1}}{2}, \frac{z-z^{-1}}{2i}\right)
Démonstration

Prenons pour contour γ le cercle C(0,1) paramétré comme suit :

\gamma : [0, 2\pi] \to \mathbb C, \gamma(t) = e^{it}

on a alors :

\oint_\gamma f(z) dz = \int_0^{2\pi} {1\over ie^{it}}R(\cos(t), \sin(t))\cdot ie^{it}dt = I

où l'on a utilisé la formule d'Euler pour passer des exponentielles complexes aux fonctions trigonométriques. Par ailleurs, le théorème des résidus nous indique que cette intégrale vaut :

\oint_\gamma f(z) dz = 2i\pi \sum_{z_j \in F} \mathrm{Res}(f, z_j)\mathrm{Ind}_\gamma(z_j) = 2i\pi \sum_{|z_j|<1} \mathrm{Res}(f, z_j)
où F désigne l'ensemble (fini) des points singuliers de f inclus dans le disque ouvert D(0,1). En égalant les deux dernières relations obtenues, on retrouve l'identité de départ.
 
Exemple

Problème : calculer l'intégrale suivante :

I = \int_0^{2\pi} \frac{ dx}{a+\sin(x) }\,,\,\,(a>1)

Solution : on est bien dans les conditions mentionnées plus haut, on a donc :

I = {2\pi\over \sqrt{a^2-1}}

Développement : La fonction rationnelle correspondante est :

R(x, y) = {1\over a+y}

on construit donc la fonction f correspondante pour le calcul de résidu :

f(z) = {1\over iz} R\left({z+z^{-1}\over 2}, {z-z^{-1}\over 2}\right) = {2\over z^2+2iaz-1}=\frac1{i\sqrt{a^2-1}}\left(\frac1{z-p_-}-\frac1{z-p_+}\right)~,

les deux pôles simples étant :

p_\pm = -i(a\pm\sqrt{a^2-1})

Le pôle p + est en dehors du cercle unité ( | p + | > 1) et ne doit donc pas être considéré ; le pôle p − = − 1 / p + est à l'intérieur ( | p − | < 1).

Le résidu de f en ce pôle est :

\mathrm{Res}(f, p_-) = \lim_{z\to p_-} (z-p_-)f(z) = {1\over i\sqrt{a^2-1}}

Il nous reste maintenant à appliquer la formule de départ :

I = 2i\pi \mathrm{Res}(f, p_-) = {2\pi\over \sqrt{a^2-1}}
 

Second type

Figure 1: Illustration du contour γ (en bleu) utilisé dans la démonstration des intégrales du second type. Les singularités (purement complexes) de f appartenant au plan supérieur sont représentées en rouge.

Soit le calcul de l'intégrale réelle suivante :

I = \int_{-\infty}^{+\infty} f(x) dx

avec f(z) ayant un ensemble de points singuliers isolés zj purement complexes. Si \exists M, R >0 et α > 1 tels que |f(z)| \le {M\over |z|^\alpha} pour tout |z| \ge R , alors

\int_{-\infty}^{+\infty} |f(x)|dx <+\infty

et

I = 2i\pi\sum_{\Im(z_j)>0}\mathrm{Res}(f, z_j) = -2i\pi\sum_{\Im(z_j)<0}\mathrm{Res}(f, z_j)

Remarque : dans le cas où f est une fonction rationnelle définie par f(z) = {P(z)\over Q(z)} avec P et Q des polynômes, il suffit d'exiger que \mathrm{deg}(Q) \ge \mathrm{deg}(P)+2 (où deg représente le degré du polynôme) pour vérifier les hypothèses et appliquer l'identité.

Démonstration
  • On a :
\int_R^{+\infty}|f(x)|dx \le M \int_R^{+\infty} {dx\over x^\alpha} = M\cdot {R^{1-\alpha}\over \alpha-1} < +\infty

où la dernière inégalité vient du fait que α > 1.

L'argument est le même pour l'intégrale de -\infty à − R. Comme la fonction n'a pas de point singulier réel, elle est bornée de -R à R et par conséquent,

\int_{-\infty}^{+\infty} |f(x)|dx <+\infty


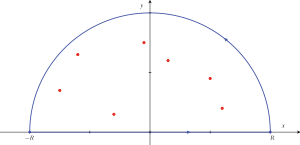
  • Soit r > R, prenons comme contour le demi cercle situé dans le demi-plan supérieur (le cas dans le demi-plan inférieur est identique) ayant pour diamètre l'intervalle [ − r,r] et illustré à la figure 1. A la limite r\to \infty , le contour entoure la totalité des points singuliers de f dans le demi-plan supérieur (leur indice par rapport au contour sera donc +1). Par le théorème des résidus, on a :
\lim_{r\to \infty} \oint_\gamma f(z) dz = 2i\pi \sum_{\Im(z_j)>0}\mathrm{Res}(f, z_j)

En décomposant le contour en ses deux parties principales, on a aussi :

\lim_{r\to \infty} = \int_{-\infty}^{+\infty} f(x) dx + \lim_{r\to \infty}\int_0^{\pi}f\left(re^{it}\right)ire^{it}dt

Or en utilisant le lemme d'estimation, on a :

\lim_{r\to\infty}\left|\int_0^{\pi}f\left(re^{it}\right)ire^{it}\mathrm{d}t\right| \le \lim_{r\to \infty}\left(\pi r\cdot \max_{|z|=r}|f\left(re^{it}\right)| \right) \le \lim_{r\to\infty}\left({\pi r M\over r^{\alpha}}\right) = 0
où dans la dernière limite on a utilisé le fait que α > 1. En reprenant les relations précédentes, on retrouve l'identité de départ.
 
Exemple

Problème : calculer l'intégrale suivante par la méthode des résidus :

I = \int_{-\infty}^{+\infty} {dx\over x^2+a^2}\,,\,\,(a>0)

Solution : cette fonction a une primitive réelle (la fonction arctangente) et la solution immédiate est I = {\pi\over a}

Développement : la fonction admet deux pôles simples p_{1,2} = \pm ia. Un seul de ces deux pôles est compris dans le plan supérieur, on a donc :

I = 2i\pi\cdot\mathrm{Res}(f, ia)

avec

\mathrm{Res}(f, ia) = \lim_{z\to ia} {z-ia\over z^2+a^2} = {1\over 2ia}
on vérifie donc que I = {\pi\over a} ainsi que prévu.
 

Troisième type

Figure 2: Illustration du contour γ (en bleu) utilisé dans la démonstration des intégrales du troisième type. Les points singuliers (purement complexes) de f appartenant au plan supérieur sont représentés en rouge.

Soit le calcul de l'intégrale réelle suivante :

I = \int_{-\infty}^{+\infty} f(x) \mathrm{e}^{iax}dx

avec f(z) comportant un ensemble de point singuliers isolés purement complexes. Si \exists M, R >0 tels que |f(z)| \le \frac{M}{|z|} pour tout |z|\ge R , alors :

(\mathrm{si}\,\,a>0),\quad I = 2i\pi \sum_{\Im(z_j)>0} \mathrm{Res}\left(f(z)\mathrm{e}^{iaz}, z_j\right)

et

(\mathrm{si}\,\,a<0),\quad I = -2i\pi \sum_{\Im(z_j)<0} \mathrm{Res}\left(f(z)\mathrm{e}^{iaz}, z_j\right)
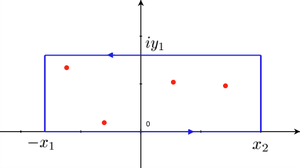
Démonstration

Supposons que a > 0 et considérons le contour γ illustré à la figure 2 l'autre cas (a<0) est identique (on prend le contour dans le plan inférieur). Posons que ce contour va de − x1 à x2 et de 0 à iy1. Posons encore que x_1, x_2, y_1 \ge R, en faisant tendre R vers l'infini, le contour encadrera donc toutes les singularités du demi-plan supérieur avec un indice +1. Le théorème des résidus nous donne :

\lim_{R\to \infty} \oint_\gamma f(z) dz = 2\pi i \sum_{\Im(z_j) > 0} \mathrm{Res}\left( f(z)\mathrm{e}^{iaz}, z_j \right)

En décomposant l'intégrale en ses quatre parties principales que l'on notera Ii avec I1 l'intégrale le long du segment x2 + iy, I2 le long du segment x + iy1 et I3 symétrique à I1. I4 représente (à la limite) l'intégrale réelle que l'on souhaite calculer.

On montre que, à la limite, l'intégrale le long des trois segments I1,I2,I3 de la fonction est nulle ce qui termine la démonstration.

On peut, en effet, majorer les différentes parties comme suit :

|I_1| \le \int_0^{y_1}|f(x_2+iy)|\mathrm{e}^{-ay}dy

en utilisant l'hypothèse, on a cependant :

|f(x_2+iy)| \le {M\over |x_2+iy|} \le {M\over x_2}

Par conséquent,

|I_1| \le {M\over x_2} \int_0^{y_1}\mathrm{e}^{-ay}dy = {M\over ax_2}(1-\mathrm{e}^{-ay_1}) \le {M\over ax_2}

la limite R\to \infty de cette intégrale vaut zéro puisque a > 0 et x_2 \ge R . L'argument développé ci-dessus est identique pour I3.

Il reste I2 qui n'est pas très différente :

|I_2| \le \int_{-x_1}^{x_2} |f(x+iy_1)|\mathrm{e}^{-ay_1}dx \le {M\over y_1}\mathrm{e}^{-ay_1}

la limite à R \to \infty est nulle puisque y_1 \ge R.

Ceci clôt la démonstration.
 
Exemple

Problème : calculer l'intégrale suivante :

I = \int_{-\infty}^{+\infty} {\mathrm{e}^{bix}dx\over a^2+x^2}\quad (a, b >0)

Solution : en appliquant le résultat ci-dessus, on obtient que :

I = {\pi\over a}\exp(-ab)

Remarque, la partie réelle de l'intégrale est \int_{-\infty}^{+\infty}{\cos(bx)\over a^2+x^2}dx et cette intégrale vaut précisément I puisque la solution par le théorème des résidus est réelle.

Développement : la fonction f(z) = (a2 + z2) − 1 a un seul pôle dans le plan supérieur, à savoir p1 = + ia. Le résidu en ce point est :

\mathrm{Res}\left( f(z)\mathrm{e}^{ibz}, +ia \right) = \lim_{z\to ia} \left( (z-ia){\mathrm{e}^{ibz}\over a^2+z^2} \right) = {e^{-ab}\over 2ai}

en appliquant la formule, on a donc :

I = 2\pi i \cdot {e^{-ab}\over 2ai} = {\pi\over a}\exp(-ab)
 

Quatrième type

Figure 3: Illustration du contour γ (en bleu) utilisé dans la démonstration des intégrales du quatrième type. Les singularités (purement complexes) de f appartenant au plan supérieur sont représentées en rouge. En vert ce sont les pôles simples réels.

Les intégrales du second et du troisième type s'étendent aux cas avec un nombre fini n de pôles situés sur l'axe réel. Il s'agit alors d'une intégrale impropre et l'on considère alors la valeur principale de Cauchy de l'intégrale.

Soit f une fonction holomorphe sur \mathbb C sauf en un ensemble de pôles simples réels, xj, et de singularités isolées purement complexes, zj. Supposons que l'on se trouve dans un des deux cas suivant :

  • \exists M, R > 0 et α > 1 tels que |f(z)| \le {M\over |z|^{\alpha}} pour tout |z|\ge R ,

ou

  • f(z) = g(z)eiaz avec a > 0 et si \exists M, R > 0 tels que |g(z)| \le {M\over |z|} pour tout |z|\ge R

alors la valeur principale de Cauchy (notée v.p.) de l'intégrale existe et on a :

\mathrm{v.p.} \int_{-\infty}^{+\infty} f(x) dx = 2\pi i \sum_{\Im(z_j)>0} \mathrm{Res}(f, z_j) + \pi i \sum_{x_j}\mathrm{Res}(f, x_j)

Remarque : on peut aisément étendre la formule au demi-plan inférieur en changeant le signe de la première somme et en considérant uniquement les singularités purement complexe dans ce demi-plan.

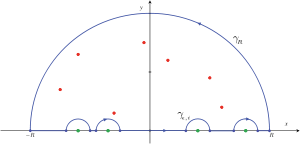
Démonstration

Soit γ le contour illustré à la figure 3, on peut décomposer ce contour en ses parties principales : notons γR le demi cercle de rayon R, \gamma_{\epsilon, j} le je demi-cercle de rayon ε contournant la singularité réelle xj et enfin \tilde{\gamma} , l'ensemble des segments situés sur l'axe réel.

A la limite R \to \infty et \epsilon \to 0, on a : \mathrm{v.p.}\int_{-\infty}^{+\infty}f(x)dx = \oint_{\tilde{\gamma}}f(z)dz.

Avec le théorème des résidus, on a :

\lim_{R\to \infty}\oint_\gamma f(z) dz = 2i\pi \sum_{\Im(z_j)>0} \mathrm{Res}(f, z_j)

et on a aussi :

\oint_{\tilde{\gamma}} f(z)dz = \oint_\gamma f(z)dz - \sum_{j=1}^{n}\oint_{\gamma_{\epsilon, j}} f(z) dz - \oint_{{\gamma_{_R}}}f(z)dz

On montre de manière identique aux deux types d'intégrations précédents que, à la limite, l'intégrale le long de γR tend vers zéro dans les deux cas considérés.

Il nous reste donc à calculer les intégrales le long des demi-cercles \gamma_{\epsilon, j} . Au voisinage d'un pôle simple réel xj, f admet un développement de Laurent sur un disque épointé centré en xj. Comme il s'agit d'un pôle simple, le seul coefficient non nul de la partie singulière du développement est a − 1,j. Autrement dit, sur ce voisinage, on peut écrire :

f(z) = {a_{-1, j}\over z-x_j} + h_j(z)

avec hj une série entière (donc une fonction holomorphe).

On a donc :

\oint_{\gamma_{\epsilon, j}}f(z)dz = \oint_{\gamma_{\epsilon, j}}{a_{-1, j}\over z-x_j}dz + \oint_{\gamma_{\epsilon, j}}h_j(z)dz

La deuxième intégrale tend vers zéro à la limite \epsilon \to 0 puisque hj est holomorphe. En explicitant l'intégrale restante, on a en considérant la paramétrisation suivante des demi-cercles :

\gamma_{\epsilon, j} : [0, \pi] \to \mathbb C, \gamma_{\epsilon, j}(t) = x_j + \epsilon \mathrm{e}^{i(\pi-t)}

où le terme π − t vient du fait que ces contours sont parcourus dans le sens anti-trigonométrique,

\oint_{\gamma_{\epsilon, j}} f(z) dz = a_{-1, j}\int_0^\pi {-i\epsilon\mathrm{e}^{i(\pi-t)}\over \epsilon\mathrm{e}^{i\pi -t}}dt = -i\pi a_{-1,j}

Le coefficient a − 1,j est par définition le résidu de la fonction en xj. A la limite R\to \infty et \epsilon \to 0 , on a donc bien :

\mathrm{v.p.}\int_{-\infty}^{+\infty}f(x)dx = \oint_{\tilde{\gamma}}f(z)dz = 2i\pi \sum_{\Im(z_j)>0} \mathrm{Res}(f, z_j) + i\pi\sum_{x_j} \mathrm{Res}(f, x_j)
 
Exemple

Problème : calculer avec a \in \mathbb R et b > 0 :

I^* = \mathrm{v.p.}\int_{-\infty}^{+\infty}{e^{ibx}\over x-a}dx

Solution : en appliquant le résultat ci-dessus, on obtient que :

I * = iπcos(ab) − πsin(ab)

Remarque, en considérant respectivement la partie réelle et imaginaire de l'intégrale on obtient :

\mathrm{v.p.}\int_{-\infty}^{+\infty}{\cos(bx)\over x-a}dx = -\pi\sin(ab)
\mathrm{v.p.}\int_{-\infty}^{+\infty}{\sin(bx)\over x-a}dx = \pi\cos(ab)

et dans le cas particulier a = 0 et b = 1, la deuxième intégrale est l'intégrale de la fonction Sinus cardinal (première définition) et vaut π. Il ne s'agit par ailleurs pas d'une intégrale impropre puisque la fonction sinc est partout définie.

Développement : la fonction a un pôle simple réel x1 = a, le résidu en ce point est :

Res(f,a) = eiab = cos(ab) + isin(ab)

en appliquant la formule on a donc bien :

I * = iπcos(ab) − πsin(ab)
 

Application aux calculs de sommes

Le théorème des résidus permet aussi de calculer certaines sommes infinies. Soit une fonction g ayant pour chaque entier n un résidu égal au n-ème terme général d'une somme infinie S ainsi qu'un ensemble E de résidus correspondant à d'autres points. Supposons que l'intégrale de cette fonction le long d'un lacet γ rectifiable infiniment grand soit nulle. On a alors par le théorème des résidus :

\int_{\gamma} g(z) \mathrm{d}z = 2i\pi \left[S + \sum_{z_k\in E} \mathrm{Res}(g;z_k)\right] = 0

Par conséquent, on peut exprimer la somme infinie par une autre somme (en général finie) de résidus :

S = -\sum_{z_k\in E} \mathrm{Res}(g; z_k)

les énoncés ci-dessous donnent des exemples plus généraux de cas pour lesquels cette méthode est applicable :

  • Les sommes du "premier type" : \sum f(n)
  • Les sommes du "second type" : \sum (-1)^n f(n)

Premier type

Soit le calcul de la somme suivante :

S = \sum_{-\infty, n\notin E}^{\infty} f(n)

avec f(z) ayant un ensemble E de singularités isolées. Supposons que la condition suivante soit respectée :

\exists M, R > 0 et α > 1 tels que |f(z)|\le {M\over |z|^\alpha} pour tout |z|\ge R

alors, nous avons :

\sum_{-\infty, n\notin E}^{\infty}|f(n)| < +\infty

et

\sum_{-\infty, n\notin E}^\infty f(n) = -\sum_{z_k\in E}\mathrm{Res}\left(f(z)\pi\cot(\pi z); z_k\right)
Démonstration
  • On a
\sum_{n\ge R, n\notin E} |f(n)| \le M\sum_{n\ge R, n\notin E} {1\over |z|^\alpha}

en utilisant le test intégral de convergence on observe que cette somme converge. On utilise le même argument pour montrer que la somme \sum_{n\le -R, n\notin E}|f(n)| converge. Comme on évite l'ensemble E des singularités de f dans la somme, on a que

\sum_{n\ge -R, n\notin E}^{n\le R}|f(n)|<+\infty (somme finie de termes bornés) et donc finalement : \sum_{-\infty, n\notin E}^\infty |f(n)| < +\infty
  • Il faut trouver une fonction g dont les résidus soient \left\{f(n), n\in \mathbb Z\right\} . Supposons que g(z) = f(z)φ(z), il faut alors que la fonction φ ait un pôle simple de résidu 1 à chaque entier. Une fonction ayant cette propriété est donnée par :
\varphi(z) = \pi{\cos(\pi z)\over \sin(\pi z)} = \pi \cot(\pi z)

en effet, sin(πz) admet un zéro simple pour chaque z entier et

\mathrm{Res}\left(\pi {\cos(\pi z)\over \sin(\pi z)} ; n\right) = {\pi \cos (\pi n) \over \sin'(\pi n)} = \pi{\cos(\pi n)\over \cos(\pi n) } =1

où l'on a utilisé la formule du résidu pour une fraction ayant un zéro simple au dénominateur.

Prenons pour contour le cercle centré à l'origine et de rayon R = N + 0.5 avec N\in \mathbb N et l'incrément d'un demi montrant que l'on évite les pôles situés en \pm N.

A la limite, le théorème des résidus donne :

\lim_{N\to \infty}\int_{C(0, R)} f(z) \pi \cot(\pi z) \mathrm{d}z = 2\pi i \lim_{N\to \infty}\left[\sum_{-N, n\notin E}^N f(n) + \sum_{z_k\in E}\mathrm{Res}\left(f(z)\pi\cot(\pi z) ; z_k\right)\right]

Il nous reste maintenant à montrer que cette limite est nulle pour obtenir le résultat voulu. En utilisant le lemme d'estimation, on a :

L = \lim_{N\to \infty}\left|\int_{C(0, R)} f(z)\pi\cot(\pi z)\mathrm{d}z\right| \le \lim_{N\to\infty}\left(2\pi R\cdot \max_{|z|=R}\left|\pi f(R\mathrm{e}^{it})\cot({\pi R\mathrm{e}^{it}})\right|\right)

Le module de la fonction cot  est bornée par une certaine constante K>0 sur le contour puisque l'on évite les entiers de l'axe réel de par le choix du contour, le membre de droite de l'inégalité ci-dessus est donc majoré par

L \le \lim_{N\to \infty} {2\pi R M K\over R^\alpha} = 0
où l'on a utilisé le fait que α > 1. Comme la limite vaut bien zéro, le résultat est démontré.
 
Exemple

Problème : calculer la somme suivante :

S = \sum_{-\infty}^{\infty} {1\over n^2+a^2}, \quad (a\in \mathbb R_0)

Solution : en appliquant le résultat ci-dessus, on obtient que :

S = {\pi\coth (\pi a)\over a}

Développement  : la fonction remplit clairement les conditions et a deux pôles simples en \pm ai , on a donc :

S = -\left(\mathrm{Res}\left({\pi\cot(\pi z)\over z^2+a^2} ; +ai\right)+\mathrm{Res}\left({\pi\cot(\pi z)\over z^2+a^2}; -ai\right)\right)

Les résidus se calculent aisément puisque ce sont des pôles simples et on a :

\mathrm{Res}\left({\pi\cot(\pi z)\over z^2+a^2}; \pm ai\right) = \lim_{z\to \pm ai} \left((z\mp ai)\cdot{\pi\cot(\pi z)\over z^2+a^2}\right) = {\pi \cos (a\pi i)\over 2ai\sin(a\pi i)}

On a donc

S = -{\pi \cos (a\pi i)\over ai\sin(a\pi i)} = {\pi\over ai}\cdot {\mathrm{e}^{i(ai\pi)} + \mathrm{e}^{i(-ai\pi)} \over 2}\cdot {2i \over \mathrm{e}^{i(ai\pi)} - \mathrm{e}^{i(-ai\pi)}} = {\pi\over a}\cdot {e^{-a\pi}+e^{a\pi}\over e^{-a\pi}-e^{-a\pi}}

et finalement

S = {\pi \coth(a\pi)\over a}

où l'on a utilisé la formule d'Euler pour passer des fonctions trigonométriques à des exponentielles complexes ainsi que la définition de la fonction cotangente hyperbolique.

Remarque : par symétrie, on a que :

\sum_{-\infty}^{-1} {1\over n^2+a^2} = \sum_{1}^{\infty}{1\over n^2+a^2} = {1\over 2}\left({\pi \coth(a\pi)\over a} - {1\over a^2}\right)
c'est-à-dire la moitié de la somme précédemment calculée moins le terme pour n=0.
 

Second type

Soit le calcul de la somme suivante :

S = \sum_{-\infty, n\notin E}^{\infty} (-1)^n f(n)

avec f(z) ayant un ensemble E de singularités isolées. Supposons que f satisfasse à la même condition que pour les sommes du premier type à savoir :

\exists M, R > 0, \alpha > 1 tels que |f(z)|\le {M\over|z|^\alpha} pour tout |z|\ge R .

alors, la somme converge absolument et on a :

\sum_{\infty, n\notin E}^{\infty}(-1)^n f(n) = -\sum_{z_k\in E} \mathrm{Res}\left(f(z)\pi\csc(\pi z); z_k\right)
Démonstration

La démonstration est identique à celle du premier type, il nous suffit de montrer que la fonction πcsc(πz) a pour résidus \left\{(-1)^n ; n\in \mathbb Z \right\} .

On a \csc(\pi z) = {1\over \sin(\pi z)} avec un pôle simple à chaque point entier.

Le résidu d'une fraction ayant un zéro simple au dénominateur est donné par :

\mathrm{Res}\left({\pi\over\sin(\pi z); n}\right)={\pi\over \sin'(n\pi)}={\pi\over \pi\cos(n\pi)} = (-1)^n
ce qui conclut la démonstration.
 
Exemple

Problème : calculer la somme suivante :

S = \sum_{n=1}^\infty {(-1)^n\sin(n\theta)\over n^3},\quad(-\pi\le\theta\le\pi)

Solution : en utilisant le résultat ci-dessus, on a :

S = {\theta(\theta^2-\pi^2)\over 12}

Développement : la fonction remplit clairement les conditions et a un pôle triple à l'origine, la façon la plus simple d'obtenir le résidu est d'utiliser un développement en série autour de l'origine :

{1\over z^3}\cdot\sin(z\theta)\cdot{\pi\over \sin(\pi z)} = {1\over z^3}\cdot\left(z\theta -{z^3\theta^3\over 6}+\dots\right)\cdot\left({1\over z}+{\pi^2z\over 6}+\dots\right)

Le résidu est, par définition, le coefficient du terme en z − 1 du développement ci-dessus c'est-à-dire :

\mathrm{Res}\left({\sin(z\theta) \pi\over z^3 \sin(\pi z)}; 0\right) = {\pi^2\theta\over 6}-{\theta^3\over 6} = {\theta\over 6}(\pi^2-\theta^2)

Nous avons donc :

\sum_{-\infty, n\neq 0}^{\infty} (-1)^n{\sin(n\theta)\over n^3} = {\theta\over 6}(\theta^2-\pi^2) = 2S

où la dernière égalité s'obtient en considérant la symétrie de la somme.

Nous avons donc bien :

S = {\theta(\theta^2-\pi^2)\over 12}
 

Voir aussi

Références

  • Murray R. SPIEGEL, Variables Complexes, Schaum, (ISBN 2-7042-0020-3)
  • Serge LANG, "Complex Analysis", 4th edition, Springer, 1999, (ISBN 0-387-98592-1)
  • Joseph BAK, Donald J. NEWMAN, "Complex Analysis", 2nd edition, Springer, 1997, (ISBN 0-387-94756-6)
  • Henri Cartan, Théorie élémentaire des fonctions analytiques, Hermann, Paris, 1961

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Théorème des résidus de Wikipédia en français (auteurs)

Игры ⚽ Нужен реферат?

Regardez d'autres dictionnaires:

  • Theoreme des residus — Théorème des résidus Le théorème des résidus en analyse complexe est un outil puissant pour évaluer des intégrales curvilignes de fonctions holomorphes sur des courbes fermées ; il peut aussi bien être utilisé pour calculer des intégrales de …   Wikipédia en Français

  • Théorème des nombres premiers — En mathématiques, et plus précisément en théorie des nombres, le théorème des nombres premiers est un résultat concernant la distribution asymptotique des nombres premiers. Sommaire 1 Énoncé du théorème 2 Histoire 3 Ébauche de la preuve …   Wikipédia en Français

  • Theoreme des deux carres de Fermat — Théorème des deux carrés de Fermat Pierre Fermat En mathématiques, le théorème des deux carrés de Fermat énonce les conditions pour qu’un nombre entier soit la somme de deux carrés parfaits (c est à dire de deux carrés d’entiers) et précise de… …   Wikipédia en Français

  • Théorème des deux carrés — de Fermat Pierre Fermat En mathématiques, le théorème des deux carrés de Fermat énonce les conditions pour qu’un nombre entier soit la somme de deux carrés parfaits (c est à dire de deux carrés d’entiers) et précise de combien de façons… …   Wikipédia en Français

  • Théorème des deux carrés de fermat — Pierre Fermat En mathématiques, le théorème des deux carrés de Fermat énonce les conditions pour qu’un nombre entier soit la somme de deux carrés parfaits (c est à dire de deux carrés d’entiers) et précise de combien de façons différentes il peut …   Wikipédia en Français

  • Méthode des résidus —  Ne doit pas être confondu avec Théorème des résidus. La méthode des résidus est appliquée en biologie, surtout dans la recherche. Elle est plus une méthode de découverte qu une méthode de démonstration, elle doit être vérifiée par la… …   Wikipédia en Français

  • Théorème des deux carrés de Fermat — Pierre Fermat En mathématiques, le théorème des deux carrés de Fermat énonce les conditions pour qu’un nombre entier soit la somme de deux carrés parfaits (c est à dire de deux carrés d’entiers) et précise de combien de façons différentes il peut …   Wikipédia en Français

  • Theoreme de Jordan — Théorème de Jordan La courbe de Jordan (en noir) divise le plan en deux régions : un « intérieur » (en bleu) et un « extérieur » (en rose). Ce résultat porte le nom de théorème de Jordan. En mathématiques, le théorème de… …   Wikipédia en Français

  • Théorème de Jordan-Brouwer — Théorème de Jordan La courbe de Jordan (en noir) divise le plan en deux régions : un « intérieur » (en bleu) et un « extérieur » (en rose). Ce résultat porte le nom de théorème de Jordan. En mathématiques, le théorème de… …   Wikipédia en Français

  • Théorème de jordan — La courbe de Jordan (en noir) divise le plan en deux régions : un « intérieur » (en bleu) et un « extérieur » (en rose). Ce résultat porte le nom de théorème de Jordan. En mathématiques, le théorème de Jordan est un… …   Wikipédia en Français

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”