Résidu à l'infini

En analyse complexe, le résidu à l'infini est le résidu d'une fonction holomorphe sur une couronne de rayon extérieur infini. L'infini ${}^\infty$ étant un point ajouté à l'espace localement compact ${}^\C$ pour le rendre compact (il s'agit alors d'une compactification par un point). Cet espace compactifié noté $\hat{\C}$ est identifié à la sphère de Riemann^[1].

Soit f une fonction holomorphe sur la couronne ${}^{A(0, R, \infty)}$ .

On définit le résidu à l'infini de la fonction $f$ comme suit :

$\mathrm{Res}(f,\infty) = \mathrm{Res}\left( {-1\over z^2}f\left({1\over z}\right), 0 \right).$

Intuitivement, on passe de l'étude de $f (z)$ à l'infini à l'étude de $f (1 / z)$ à l'origine.

Par ailleurs, pour tout $r > R$ , on a :

$\mathrm{Res}(f, \infty) = {-1\over 2\pi i}\int_{C(0, r)} f(z)~\mathrm dz.$

Les relations ci-dessus permettent de renforcer le théorème des résidus pour calculer certaines intégrales réelles.

Preuve des équivalences

Tel qu'on l'a défini plus haut et en effectuant le changement de variable $w = z - 1$ pour passer de $f (w)$ à $f\left(z^{-1}\right)$ , on a :

$\mathrm{Res}(f, \infty) = {1\over 2\pi i}\int_{C(0, r')} {-1\over z^2}f\left({1\over z}\right)~\mathrm dz$

où l'on a considéré la définition d'un résidu. L'intégrale est indépendante de r' tel que $0 < r' < R - 1$ et on peut donc considérer en particulier le cas $r' = r - 1$ (avec $r > R$ comme indiqué plus haut).

Le membre de droite prouve la première équivalence puisqu'il correspond à $\mathrm{Res}\left( {-1\over z^2}f\left({1\over z}\right), 0 \right)$ .

On peut développer l'intégrale en considérant la paramétrisation habituelle du cercle : $z = r - 1 exp(i t)$ :

$\int_{C(0,1/r)}{-1\over z^2}f\left({1\over z}\right)~\mathrm dz=\int_0^{2\pi} -r^2e^{-2it}f\left(re^{-it}\right){i\over r}e^{it}~\mathrm dt.$

Or cette dernière expression est égale à :

$\int_0^{2\pi}f\left(re^{-it}\right)\cdot\left(-ire^{-it}\right)~\mathrm dt=\int_{C^*(0, r)}f(z)~\mathrm dz$

où l'exposant * indique que le chemin est parcouru dans le sens opposé (sens anti-trigonométrique). En insérant ce dernier résultat dans l'équation de départ, nous avons finalement :

$\mathrm{Res}(f,\infty)={-1\over 2\pi i}\int_{C(0,r)}f(z)~\mathrm dz$

où l'on a utilisé la propriété des intégrales curvilignes indiquant que la valeur de l'intégrale d'une fonction holomorphe le long d'un chemin $γ$ est opposée à la valeur de l'intégrale sur ce même chemin parcouru dans le sens opposé $γ *$ .

Application

Illustration du contour

γ

en ses quatre parties (demi cercle droit, demi cercle gauche, segment inférieur et segment supérieur)

Ce théorème peut s'avérer efficace dans le calcul d'intégrales définies. Considérons par exemple de calculer par le biais des résidus l'intégrale suivante :

$I=\int_{-1}^1{\mathrm dx\over \sqrt{1-x^2}}.$

L'intégrale peut être calculée en utilisant les méthodes habituelles de l'analyse réelle et le résultat est $I = π$ .

On considère une détermination holomorphe de $\sqrt{1-z^2}$ sur l'ouvert simplement connexe $U =\C\backslash [-1, 1]$ :

$\sqrt{1-z^2} = \sqrt{1-z}\sqrt{1+z} = \sqrt{|1-z|}\mathrm{e}^{i\theta_1/2}\sqrt{|1+z|}\mathrm{e}^{i\theta_2/2}$

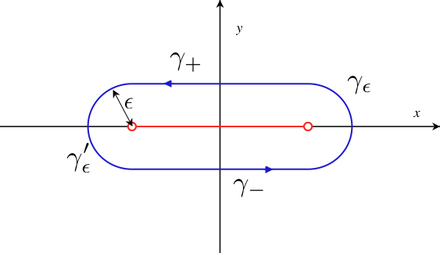
avec $\theta_1 \in[0, 2\pi[$ et $\theta_2\in [-\pi, \pi[$ (c-à-d. la détermination principale).

soit le contour $γ$ entourant la discontinuité et illustré sur la figure. Il est clair que ce contour est homotope au cercle centré à l'origine et de rayon R>1 $C (0, R)$ . On a donc :

$I^*=\int_\gamma f(z)~\mathrm dz=\int_{C(0,R)}f(z)~\mathrm dz=-2i\pi\mathrm{Res}(f,\infty).$

Commençons par calculer le résidu à l'infini :

$\mathrm{Res}(f, \infty) = \mathrm{Res}\left( {-1\over z^2}f\left({1\over z}\right),0\right)$

où l'on a :

${-1\over z^2} f\left({1\over z}\right) = {-1\over z^2}\cdot {1\over \sqrt{1-1/z^2} } = {-1\over z\sqrt{z^2-1}}.$

Le résidu vaut donc :

$\mathrm{Res}(f,\infty) = \lim_{z\to 0} z\cdot {-1\over z\sqrt{z^2-1}} = i.$

Par conséquent on a :

I * = 2π.

Il reste à passer à la limite $\epsilon \to 0$ ; en décomposant l'intégrale en quatre chemins illustrés à la figure ci-contre, on a :

$\lim_{\epsilon \to 0}\int_\gamma f(z)~\mathrm dz=\lim_{\epsilon\to 0}\left(\int_{\gamma_+\circ \gamma_-}f(z)~\mathrm dz+\int_{\gamma_\epsilon\circ\gamma'_\epsilon}f(z)~\mathrm dz\right).$

Par estimation standard, on montre que le deuxième terme du membre de droite tend vers zéro à la limite. Par ailleurs, lorsque $\epsilon\to 0$ , le long de $γ +$ , $θ 1$ et $θ 2$ tendent vers $π$ ; le long de $γ -$ , $θ 1$ tend vers $π$ et $θ 2$ vers $- π$ , on a donc :

$\lim_{\epsilon\to 0} \int_{\gamma_+}{\mathrm{d}z\over \sqrt{|1-z|}\mathrm{e}^{i\theta_1/2}\sqrt{|1+z|}\mathrm{e}^{i\theta_2/2}} = \int_{+1}^{-1}{-\mathrm{d}x\over \sqrt{1-x^2}}$

avec $e i (π + π) / 2 = e i π = - 1$ et

$\lim_{\epsilon\to 0}\int_{\gamma_-}f(z)~\mathrm dz=\int_{-1}^{+1}{\mathrm dx\over \sqrt{1-x^2}}=I$

avec $e i (π - π) / 2 = 1$ .

On a finalement :

$I^*=\lim_{\epsilon\to 0}\left(\int_{\gamma_+}f(z)~\mathrm dz+\int_{\gamma_-}f(z)~\mathrm dz\right)=2I$

et nous avons bien le résultat espéré, à savoir $I = π$ .

Il était ici beaucoup plus aisé de passer par l'analyse réelle mais la méthode présentée ci-dessus peut être utilisée dans des cas pour lesquels une forme analytique simple n'existe pas. L'exemple ci-dessus a cependant l'avantage d'être représentatif et relativement simple.

Références

↑ Michèle Audin, Analyse Complexe, notes de cours de l'université de Strasbourg, p. 70-72

Murray R. Spiegel, Variables complexes, McGraw-Hill, 1973 (ISBN 978-2-7042-0020-7)
Henri Cartan, Théorie élémentaire des fonctions analytiques d'une ou plusieurs variables complexes, Hermann, 1961

Article connexe

Fonction multivaluée

Portail de l'analyse

Catégorie :

Analyse complexe

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Résidu à l'infini de Wikipédia en français (auteurs)

Игры ⚽ Нужно сделать НИР?

Regardez d'autres dictionnaires:

Théorème des résidus — Le théorème des résidus en analyse complexe est un outil puissant pour évaluer des intégrales curvilignes de fonctions holomorphes sur des courbes fermées ; il peut aussi bien être utilisé pour calculer des intégrales de fonctions réelles… … Wikipédia en Français
Projet:Mathématiques/Liste des articles de mathématiques — Cette page n est plus mise à jour depuis l arrêt de DumZiBoT. Pour demander sa remise en service, faire une requête sur WP:RBOT Cette page recense les articles relatifs aux mathématiques, qui sont liés aux portails de mathématiques, géométrie ou… … Wikipédia en Français
Theoreme des residus — Théorème des résidus Le théorème des résidus en analyse complexe est un outil puissant pour évaluer des intégrales curvilignes de fonctions holomorphes sur des courbes fermées ; il peut aussi bien être utilisé pour calculer des intégrales de … Wikipédia en Français
Liste des articles de mathematiques — Projet:Mathématiques/Liste des articles de mathématiques Cette page recense les articles relatifs aux mathématiques, qui sont liés aux portails de mathématiques, géométrie ou probabilités et statistiques via l un des trois bandeaux suivants … Wikipédia en Français
Sphère de Riemann — Pour les articles homonymes, voir Sphère (homonymie). En mathématiques, la sphère de Riemann est une manière de prolonger le plan des nombres complexes avec un point additionnel à l infini, de manière à ce que certaines expressions mathématiques… … Wikipédia en Français
Sphere de Riemann — Sphère de Riemann Pour les articles homonymes, voir Sphère (homonymie). En mathématiques, la sphère de Riemann est une manière de prolonger le plan des nombres complexes avec un point additionnel à l infini, de manière à ce que certaines… … Wikipédia en Français
Sphère de Gauss — Sphère de Riemann Pour les articles homonymes, voir Sphère (homonymie). En mathématiques, la sphère de Riemann est une manière de prolonger le plan des nombres complexes avec un point additionnel à l infini, de manière à ce que certaines… … Wikipédia en Français
Sphère de riemann — Pour les articles homonymes, voir Sphère (homonymie). En mathématiques, la sphère de Riemann est une manière de prolonger le plan des nombres complexes avec un point additionnel à l infini, de manière à ce que certaines expressions mathématiques… … Wikipédia en Français
Fonction multiforme — Fonction multivaluée Ce diagramme ne représente pas une vraie fonction car à l élément 3 appartenant à X correspond deux éléments dans Y : b et c. En mathématiques, une fonction multivaluée (aussi appelée multiforme) est une fonction qui… … Wikipédia en Français
Fonction multivaluée — Ce diagramme représente une multifonction : à chaque élément de X on fait correspondre une partie de Y ; ainsi à l élément 3 de X correspond la partie de Y formée des deux points b et c. En mathématiques, une fonction multivaluée (aussi … Wikipédia en Français

Dictionnaires et Encyclopédies sur 'Academic'

Résidu à l'infini

Sommaire

Preuve des équivalences

Application

Références

Article connexe

Regardez d'autres dictionnaires:

Share the article and excerpts

Dictionnaires et Encyclopédies sur 'Academic'

Wikipédia en Français

Résidu à l'infini

Sommaire

Preuve des équivalences

Application

Références

Article connexe

Regardez d'autres dictionnaires:

Share the article and excerpts

Direct link