Sinus cardinal

sinc (x): Sinus cardinal non normalisé sinc (πx): Sinus cardinal normalisé

En mathématiques, la fonction sinus cardinal est une fonction spéciale définie à partir de la fonction trigonométrique sinus, apparaissant fréquemment dans des problèmes de physique ondulatoire, et dont le graphe est communément appelé « chapeau mexicain ».

Définitions

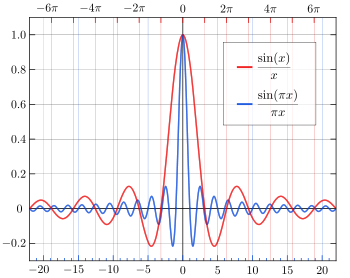
La fonction sinus cardinal est définie par :

$\operatorname{sinc}(x) = \frac{\sin(x)}{x}$ (définition 1)

où $sin$ désigne la fonction sinus.

Comme souvent en mathématiques, il existe une autre définition couramment utilisée :

$\operatorname{sinc}(x) = \frac{\sin(\pi x)}{\pi x}$ (définition 2)

Quand une confusion pourra être possible, on notera par la suite $\operatorname{sinc}_1$ (resp. $\operatorname{sinc}_\pi$ ) la première (et respectivement la seconde) version de la fonction. La seconde est parfois nommée sinus cardinal normalisé.

Propriétés

Propriétés élémentaires

La valeur en zéro semble de prime abord non définie, mais le calcul de limite est possible : on reconnaît en

$\frac{\sin x}{x}=\frac{\sin x-\sin 0}{x-0}$

un taux d'accroissement pour la fonction sinus, dont la limite en 0 est le nombre dérivé du sinus en 0, égale à $cos(0) = 1$ , ce qui permet de définir la fonction en posant sinc(0) = 1, en opérant ainsi un prolongement par continuité.

Les zéros de la fonction sont atteints en $x = k\pi,\ k \in \Z^*$ (première définition) ou $x = k,\ k \in \Z^*$ (seconde définition)

Abscisses et valeurs des extrema
$x$	$\tfrac x\pi$	$\operatorname{sinc}(x)$	$\operatorname{sinc}^2(x)$	$20\log\|\operatorname{sinc}(x)\|$
0	0	1	1	0
4.493409	1.430297	-0.217234	0.047190	-13.261459
7.725252	2.459024	0.128375	0.016480	-17.830421
10.904122	3.470890	-0.091325	0.008340	-20.788187
14.066194	4.477409	0.070913	0.005029	-22.985427
17.220755	5.481537	-0.057972	0.003361	-24.735664
20.371303	6.484387	0.049030	0.002404	-26.190829
23.519452	7.486474	-0.042480	0.001805	-27.436388
26.666054	8.488069	0.037475	0.001404	-28.525278
29.811599	9.489327	-0.033525	0.001124	-29.492589
32.956389	10.490344	0.030329	0.000920	-30.362789
36.100622	11.491185	-0.027690	0.000767	-31.153625
39.244432	12.491891	0.025473	0.000649	-31.878380
42.387914	13.492492	-0.023585	0.000556	-32.547257

La valeur où le carré de $\operatorname{sinc}_1(x)$ vaut 0,5 est atteinte pour x = +/- 1.39156 environ (ce qui permet de définir la largeur de la bande passante à -3 dB en puissance, de la fonction)

Résultats de calcul infinitésimal

La fonction est développable en série entière sur la droite réelle

$\frac{\sin x}{x}=\sum_{n=0}^{+\infty} \frac{(-1)^n x^{2n}}{(2n+1)!}$

De là vient que le sinus cardinal est indéfiniment dérivable sur $\R$ . Il peut même être étendu en une fonction holomorphe sur tout le plan complexe, en employant la formule précédente pour tout x complexe.

Les primitives de la fonction sinus cardinal ne peuvent être calculées à l'aide des fonctions élémentaires. Il est habituel de définir une fonction spéciale, la fonction sinus intégral comme la primitive du sinus cardinal nulle en 0

$\operatorname{Si}(x) = \int_0^x\frac{\sin t}{t}\,\mathrm dt$

On démontre que l'intégrale $\int_0^{+\infty}\frac{\sin x}x \,\mathrm dx$ converge. Il s'agit de l'intégrale de Dirichlet, valant $π / 2$ . Cependant la fonction sinus cardinal n'est pas intégrable sur $\R_+$ au sens de Lebesgue (ni d'ailleurs à aucun autre sens, pas même à celui de l'intégrale de jauge), car la convergence n'est pas absolue ; en d'autres termes, on a $\int_0^{+\infty}\frac{|\sin t|}{t}\,\mathrm dt=+\infty$ .

Transformée de Fourier

La transformée de Fourier du sinus cardinal est la fonction porte:

$\int_{-\infty}^\infty \operatorname{sinc}_\pi(t)e^{-2\pi i f t}\,\mathrm dt = \operatorname{rect}_1(f)$

où la fonction porte est définie de la manière suivante :

$\operatorname{rect}_\tau \left(t\right) = \begin{cases}1 & |t|\le\tau/2 \\ 0 & \text{sinon} \end{cases}$ .

La transformée de Fourier de la fonction porte telle que définie ci-dessus est également un sinus cardinal:

$\mathcal F(\operatorname{rect}_\tau)(\omega) = \frac1{\sqrt{2\pi}}\int \limits_{-\tau/2}^{\tau/2} e^{-\mathrm{i} \omega t} \,\mathrm dt = \frac1{\sqrt{2\pi}}\tau \operatorname{sinc}_1 \left( \frac{\omega \tau}{2} \right)$ .

Utilisation et applications

E. T. Whittaker a montré que la fonction sinus cardinal joue un rôle central dans la théorie de l'interpolation sur un réseau de points équidistants^[1].
Étant donné que la transformée de Fourier de la fonction porte est très couramment utilisée, le sinus cardinal est forcément très présent, notamment en physique ondulatoire (car les phénomènes de diffraction de Fraunhofer sont traités par transformée de Fourier) ainsi qu'en traitement numérique du signal. Plus précisément, en théorie de la communication, la fonction sinus cardinal permet la synthèse exacte des signaux à spectre de support fini (formule de Shannon, 1949). En particulier, le sinus cardinal est fréquemment rencontré en théorie des antennes, en acoustique, en radar, pour la diffraction par une fente, etc.
La même idée est à la base de l’approximation sigma de Cornelius Lanczos.
On utilise également souvent le carré du sinus cardinal, car celui-ci donne l'intensité ou la puissance du signal dont l'amplitude est en sinus cardinal. Souvent, on cherchera à réduire l'influence des maxima secondaires du module (qui donne lieu à des lobes secondaires indésirables).

Étant donné que les valeurs décroissent rapidement, le carré de la fonction sinus cardinal est souvent représenté en échelle logarithmique.

Notes et références

↑ Cf. Edmund Taylor Whittaker, « On the functions which are represented by the expansions of the interpolation theory », dans Proc. Royal Soc. of Edinburgh, n^o 35, 1915, p. 181-194 ; et J. M. Whittaker, Interpolatory function theory, Londres, Cambridge University Press, coll. « Cambridge Tracts in Mathematics and Mathematical Physics », 1935 .

Voir aussi

Sur les autres projets Wikimedia :

« Sinc », sur Wikimedia Commons (ressources multimédia)

Regardez d'autres dictionnaires:

Sinus integral — Sinus intégral La fonction sinus intégral, notée Si, est une fonction spéciale de la physique mathématique introduite par Fresnel dans l étude des vibrations lumineuses, est définie par . Propriétés La fonction est continue, infiniment dérivable… … Wikipédia en Français
Sinus intégral — Ne pas confondre avec la fonction sinus cardinal. Tracé de Si(x) pour . La fo … Wikipédia en Français
Sinus (mathématique) — Fonction trigonométrique Pour les articles homonymes, voir Cosinus (homonymie), Tangente et Sinus. Toutes les valeurs des fonctions trigonométriques en u … Wikipédia en Français
Sinus (mathématiques) — Fonction trigonométrique Pour les articles homonymes, voir Cosinus (homonymie), Tangente et Sinus. Toutes les valeurs des fonctions trigonométriques en u … Wikipédia en Français
Sinus — Cette page d’homonymie répertorie les différents sujets et articles partageant un même nom. Sur les autres projets Wikimedia : « sinus », sur le Wiktionnaire (dictionnaire universel) Sinus est un mot latin signifiant… … Wikipédia en Français
Sinus venosus — This article is on an embryological structure. For the heart defect of the same name, please see atrial septal defect. Infobox Embryology Name = Sinus venosus Latin = GraySubject = 138 GrayPage = 528 Caption = Interior of dorsal half of heart… … Wikipedia
cardinal vein — noun any of the major venous channels in primitive adult vertebrates and in embryos of higher vertebrates • Hypernyms: ↑vein, ↑vena, ↑venous blood vessel • Hyponyms: ↑anterior cardinal vein, ↑posterior cardinal vein, ↑common cardinal vein … Useful english dictionary
Cardinal veins — Infobox Embryology Name = PAGENAME Latin = GraySubject = 135 GrayPage = 520 Caption = Scheme of arrangement of parietal veins. Caption2 = Human embryo with heart and anterior body wall removed to show the sinus venosus and its tributaries. System … Wikipedia
cardinal vein — a bilaterally paired longitudinal vein. The anterior cardinal vein returns blood from the head and the posterior cardinal vein from the trunk, joining together as the common cardinal vein (which is also called the duct of Cuvier or incorrectly… … Dictionary of ichthyology
cardinal veins — two pairs of veins in the embryo that carry blood from the head (anterior cardinal veins) and trunk (posterior cardinal veins); they unite to form the common cardinal vein, which drains into the sinus venosus of the heart. * * * embryonic vessels … Medical dictionary

Dictionnaires et Encyclopédies sur 'Academic'

Sinus cardinal

Sommaire

Définitions