Lemme d'estimation

En mathématiques, le lemme d'estimation (aussi appelé lemme d'estimation standard^[1]) donne un majorant (du module) d'une intégrale curviligne. Si f est une fonction à valeurs complexes, continue sur le chemin rectifiable $γ$ , on a :

$\left|\int_\gamma f(z) \mathrm{d}z \right| \le \mathrm{L}(\gamma)\max_{z\in \mathrm{Im}\, \gamma} |f(z)|$

où $L(γ)$ est la longueur du chemin rectifiable. À noter que la borne supérieure existe et est atteinte (c'est donc un maximum) car l'image d'un chemin rectifiable est compacte et f est continue.

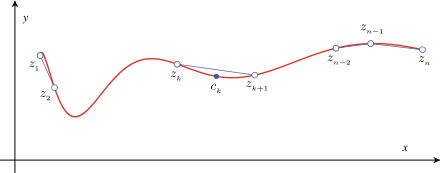Figure 1: Illustration de l'approximation de l'intégrale curviligne le long d'un contour

γ

(en rouge) par une somme des valeurs atteintes en n points

c k

appartenant à n-1 petits arcs formant le contour.
La somme des longueurs des cordes (en bleu) donne une approximation de la longueur du contour.

On peut justifier intuitivement le lemme comme suit : en subdivisant le chemin $γ$ en n-1 petits arcs d'extrémités successives $z_1,\dots, z_n$ , on approche l'intégrale curviligne par une somme de Riemann :

$I = \int_{\gamma}f(z)\mathrm{d}z\approx\sum_{k=1}^{n-1} f(c_k) (z_{k+1}-z_{k})$

où $c k$ est un point arbitraire de l'arc joignant $z k$ à $z k + 1$ . Le module de chaque terme de la somme est majoré par $M\cdot |z_{k+1} - z_{k}|$ , où M est le maximum de $| f |$ sur $γ$ et $| z k + 1 - z k |$ est la longueur de la corde joignant $z k$ à $z k + 1$ . Comme la somme des longueurs de ces cordes approche la longueur du chemin $γ$ , on peut s'attendre^{[Note 1]} à la majoration $|I| \leq M \rm{L}(\gamma)$ .

Ce lemme est très utilisé en analyse complexe pour montrer que l'intégrale le long d'une partie d'un contour tend vers zéro en passant à certaine limite. L'exemple traité infra permet d'illustrer ce principe.

Démonstration

Soit $\gamma : [a, b] \to \mathbb C, t\mapsto \gamma(t)$ , un chemin de classe $\mathcal C^1$ par morceaux, on a :

$|I| = \left|\int_\gamma f(z) \mathrm{d}z\right| = \left|\int_a^b f(\gamma(t))\gamma'(t) \mathrm{d}t\right|$

ce que l'on peut majorer comme suit :

$|I| \le \int_a^b\left|f(\gamma(t))\right|\left|\gamma'(t)\right|\mathrm{d}t$

En majorant le module de f sur le chemin et par définition de la longueur d'un arc, on a :

$|I| \leq \max_{t\in[a,b]}|f(\gamma(t))| \int_a^b \left|\gamma'(t)\right|\mathrm{d}t\text{ et }\mathrm{L}(\gamma) = \int_a^b \left|\gamma'(t)\right|\mathrm{d}t$

d'où finalement :

$|I| \leq \mathrm{L}(\gamma)\max_{z\in \mathrm{Im}\,\gamma}|f(z)|$

Exemple

Figure 2 : Illustration du chemin

γ

utilisé dans l'exemple.

Problème : trouver un majorant pour :

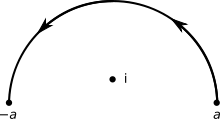
$\left|\int_\gamma {1\over(z^2+1)^2}\mathrm{d}z\right|$

où $γ$ est le demi-cercle dans le plan supérieur de rayon $a > 1$ parcouru dans le sens direct et illustré à la figure 1 ci-contre.

Solution : La longueur du chemin est la moitié du périmètre d'un cercle de rayon a, on a donc :

L(γ) = π a

On cherche ensuite un majorant M pour l'intégrande sur le chemin. Par inégalité triangulaire, on a :

$|z|^2 = |z^2+1-1| \le |z^2+1|+1$

par conséquent, sur le chemin $γ$ ,

$|z^2+1|\ge |z|^2-1 = a^2-1 > 0$

nous avons donc, $\forall z \in \gamma$ :

$\left|{1\over (z^2+1)^2}\right| \le {1\over(a^2-1)^2}=M$

En appliquant le lemme, on a :

$\left|\int_\gamma {1\over(z^2+1)^2}\mathrm{d}z\right| \le {\pi a\over (a^2-1)^2}$

Remarque, on voit qu'à la limite $a \to \infty$ , l'intégrale le long du demi-cercle tend vers zéro. Cela nous permet d'appliquer aisément le théorème des résidus pour calculer l'intégrale suivante :

$\int_{-\infty}^{+\infty} {dx\over (x^2+1)^2} = {\pi\over 2}$

où l'on a considéré le lacet obtenu en complétant $γ$ par le segment $[ - a, a]$ . En effet, la fonction a un pôle double dans le demi-plan supérieur : $z 1 = + i$ et le résidu en ce point est :

$\mathrm{Res}(f, +i) = \lim_{z\to i} \left({(z-i)^2\over (z^2+1)^2}\right)' = \frac{1}{4i}$

où la dérivée vient du fait que i est un pôle d'ordre deux. En appliquant le théorème des résidus et en considérant le résultat précédent (l'intégrale s'annule le long du demi-cercle dans le plan supérieur à la limite), on a :

$\int_{-\infty}^{+\infty} {dx\over (x^2+1)^2} = 2\pi i \cdot \frac{1}{4i} = {\pi\over 2}$

Notes

↑ en utilisant l'inégalité triangulaire, à savoir que $\left|\sum_{k=1}^n a_k\right| \le \sum_{k=1}^n |a_k|$ pour des $a k$ réels ou complexes.

Références

(en) Serge Lang, Complex Analysis, Springer, 1999, 4^e éd. (ISBN 0-387-98592-1)

↑ Michèle Audin, Analyse Complexe, notes de cours de l'université de Strasbourg

Portail de l'analyse

Catégories :

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Lemme d'estimation de Wikipédia en français (auteurs)

Игры ⚽ Нужна курсовая?

Regardez d'autres dictionnaires:

Lemme De Grönwall — En mathématiques, le lemme de Grönwall, nommé d après Thomas Hakon Grönwall (1877 1932) qui l établit en 1919, permet l estimation d une fonction qui vérifie une certaine inégalité différentielle. Le lemme existe sous deux formes, intégrale et… … Wikipédia en Français
Lemme de Gronwall — Lemme de Grönwall En mathématiques, le lemme de Grönwall, nommé d après Thomas Hakon Grönwall (1877 1932) qui l établit en 1919, permet l estimation d une fonction qui vérifie une certaine inégalité différentielle. Le lemme existe sous deux… … Wikipédia en Français
Lemme de grönwall — En mathématiques, le lemme de Grönwall, nommé d après Thomas Hakon Grönwall (1877 1932) qui l établit en 1919, permet l estimation d une fonction qui vérifie une certaine inégalité différentielle. Le lemme existe sous deux formes, intégrale et… … Wikipédia en Français
Lemme de Goursat (analyse complexe) — Ne pas confondre avec le lemme de Goursat en algèbre. En analyse complexe, le lemme de Goursat (ou théorème de Goursat) est une version faible du théorème intégral de Cauchy. Selon ce lemme, si une fonction d une variable complexe est… … Wikipédia en Français
Lemme de Grönwall — En mathématiques, le lemme de Grönwall, nommé d après Thomas Hakon Grönwall (en) qui l établit en 1919, permet l estimation d une fonction qui vérifie une certaine inégalité différentielle. Le lemme existe sous deux formes, intégrale et… … Wikipédia en Français
Lemme de Borel-Carathéodory — Ne doit pas être confondu avec Lemme de Borel Cantelli. En mathématiques, le lemme de Borel Carathéodory, nommé d après Émile Borel et Constantin Carathéodory, est un lemme estimant le maximum d une fonction analytique dans un disque centré … Wikipédia en Français
Projet:Mathématiques/Liste des articles de mathématiques — Cette page n est plus mise à jour depuis l arrêt de DumZiBoT. Pour demander sa remise en service, faire une requête sur WP:RBOT Cette page recense les articles relatifs aux mathématiques, qui sont liés aux portails de mathématiques, géométrie ou… … Wikipédia en Français
Theoreme des residus — Théorème des résidus Le théorème des résidus en analyse complexe est un outil puissant pour évaluer des intégrales curvilignes de fonctions holomorphes sur des courbes fermées ; il peut aussi bien être utilisé pour calculer des intégrales de … Wikipédia en Français
Théorème des résidus — Le théorème des résidus en analyse complexe est un outil puissant pour évaluer des intégrales curvilignes de fonctions holomorphes sur des courbes fermées ; il peut aussi bien être utilisé pour calculer des intégrales de fonctions réelles… … Wikipédia en Français
Liste des articles de mathematiques — Projet:Mathématiques/Liste des articles de mathématiques Cette page recense les articles relatifs aux mathématiques, qui sont liés aux portails de mathématiques, géométrie ou probabilités et statistiques via l un des trois bandeaux suivants … Wikipédia en Français

Dictionnaires et Encyclopédies sur 'Academic'

Lemme d'estimation

Sommaire

Démonstration

Exemple

Notes

Références

Regardez d'autres dictionnaires:

Share the article and excerpts

Dictionnaires et Encyclopédies sur 'Academic'

Wikipédia en Français

Lemme d'estimation

Sommaire

Démonstration

Exemple

Notes

Références

Regardez d'autres dictionnaires:

Share the article and excerpts

Direct link