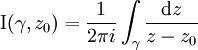Indice d'un lacet
- Indice d'un lacet
-
Lacet (mathématiques)
En mathématiques, un lacet est la modélisation d'une « boucle ». C'est une courbe continue et fermée, c'est-à-dire que ses extrémités sont confondues. La notion de lacet est utile en analyse complexe et en topologie.
Définitions
Si X est un espace topologique, on appelle lacet sur X toute application continue ![\gamma \, : \, [0,1] \rightarrow X](/pictures/frwiki/98/b5637ba65eb3449af2b37da8c21354bf.png) telle que γ(0) = γ(1).
telle que γ(0) = γ(1).
Autres définitions :
- Un lacet sur X est un chemin sur X dont l'extrémité est confondue avec l'origine.
- Un lacet sur X est une application continue de S1 vers X (où S1 dénote le cercle unité
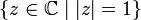 ).
).
En analyse complexe on s'intéresse aux lacets qui sont aussi des courbes rectifiables.
Un lacet f est dit simple lorsque l'égalité f(a) = f(b) implique, soit que a est égal à b, soit que a et b sont égaux à 0 et à 1. Intuitivement, cela signifie que le lacet ne dessine qu'une unique boucle. On peut aussi définir des lacets polygonaux, ou de classe Ck (voir Chemins). Les termes de lacet simple et de courbe de Jordan sont synonymes.
Dans le cas 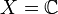 , on peut définir l'indice I(γ,z0) d'un lacet γ par rapport à un point
, on peut définir l'indice I(γ,z0) d'un lacet γ par rapport à un point ![z_0\in\mathbb{C} \smallsetminus \gamma([0, 1])](/pictures/frwiki/53/5490f0cbb667cb3f6d56543ec68ae555.png) : il correspond au nombre (entier algébrique) de tours effectués par le lacet autour de ce point.
: il correspond au nombre (entier algébrique) de tours effectués par le lacet autour de ce point.
On peut l'obtenir en calculant :
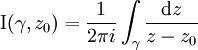
Voir aussi
 Portail des mathématiques
Portail des mathématiques
Catégories : Topologie algébrique | Analyse complexe
Wikimedia Foundation.
2010.
Contenu soumis à la licence CC-BY-SA. Source : Article Indice d'un lacet de Wikipédia en français (auteurs)
Regardez d'autres dictionnaires:
Indice (analyse complexe) — Pour les articles homonymes, voir indice. Un point z0 et une courbe C Indice d un point par rapport à un lacet … Wikipédia en Français
Lacet (mathématiques) — Pour les articles homonymes, voir Lacet. En mathématiques, un lacet est la modélisation d une « boucle ». C est un chemin continu et fermé, c est à dire que ses extrémités sont confondues. La notion de lacet est utile en analyse… … Wikipédia en Français
Indice(analyse complexe) — Indice (analyse complexe) Pour les articles homonymes, voir indice. Un point z0 et une courbe C … Wikipédia en Français
Indice — Cette page d’homonymie répertorie les différents sujets et articles partageant un même nom. Sur les autres projets Wikimedia : « Indice », sur le Wiktionnaire (dictionnaire universel) Le mot indice peut avoir plusieurs… … Wikipédia en Français
FONCTIONS ANALYTIQUES - Fonctions d’une variable complexe — On se propose, dans ce premier article, d’exposer, avec des démonstrations quasiment complètes, les résultats les plus élémentaires de la théorie des fonctions analytiques d’une variable complexe; les deux derniers chapitres sont consacrés à… … Encyclopédie Universelle
Courbe de Jordan — Théorème de Jordan La courbe de Jordan (en noir) divise le plan en deux régions : un « intérieur » (en bleu) et un « extérieur » (en rose). Ce résultat porte le nom de théorème de Jordan. En mathématiques, le théorème de… … Wikipédia en Français
Theoreme de Jordan — Théorème de Jordan La courbe de Jordan (en noir) divise le plan en deux régions : un « intérieur » (en bleu) et un « extérieur » (en rose). Ce résultat porte le nom de théorème de Jordan. En mathématiques, le théorème de… … Wikipédia en Français
Théorème de Jordan-Brouwer — Théorème de Jordan La courbe de Jordan (en noir) divise le plan en deux régions : un « intérieur » (en bleu) et un « extérieur » (en rose). Ce résultat porte le nom de théorème de Jordan. En mathématiques, le théorème de… … Wikipédia en Français
Théorème de jordan — La courbe de Jordan (en noir) divise le plan en deux régions : un « intérieur » (en bleu) et un « extérieur » (en rose). Ce résultat porte le nom de théorème de Jordan. En mathématiques, le théorème de Jordan est un… … Wikipédia en Français
Théorème de Jordan — En mathématiques, le théorème de Jordan est un théorème de topologie plane. Il est célèbre par le caractère apparemment intuitif de son énoncé et la difficulté de sa démonstration. « En fait, il n y a pratiquement aucun autre théorème qui… … Wikipédia en Français
![\gamma \, : \, [0,1] \rightarrow X](/pictures/frwiki/98/b5637ba65eb3449af2b37da8c21354bf.png) telle que γ(0) = γ(1).
telle que γ(0) = γ(1).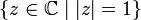 ).
).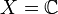 , on peut définir l'indice I(γ,z0) d'un lacet γ par rapport à un point
, on peut définir l'indice I(γ,z0) d'un lacet γ par rapport à un point ![z_0\in\mathbb{C} \smallsetminus \gamma([0, 1])](/pictures/frwiki/53/5490f0cbb667cb3f6d56543ec68ae555.png) : il correspond au nombre (entier algébrique) de tours effectués par le lacet autour de ce point.
: il correspond au nombre (entier algébrique) de tours effectués par le lacet autour de ce point.