- Théorème de stokes
-
Théorème de Stokes
 Pour les articles homonymes, voir Stokes.
Pour les articles homonymes, voir Stokes.Articles d'analyse vectorielle 
Objets d'étude Champ vectoriel Champ scalaire Équation aux dérivées partielles de Laplace de Poisson Opérateurs Nabla Gradient Rotationnel Divergence Laplacien scalaire Bilaplacien Laplacien vectoriel D'alembertien Théorèmes de Green de Stokes de Helmholtz de flux-divergence du gradient du rotationnel En géométrie différentielle, le théorème de Stokes est un résultat central sur l'intégration de formes différentielles, qui généralise nombre de théorèmes sur l'analyse vectorielle. Après l'énoncé et la démonstration, cet article en propose nombre d'applications : en particulier, il fournit un formulaire qu'utilisent volontiers physiciens et ingénieurs, particulièrement en mécanique des fluides.
Théorème de Stokes — Soit M une variété différentielle orientée de dimension n, et ω une (n-1)-forme différentielle à support compact sur M de classe C1. Alors, on a :
où d désigne la dérivée extérieure,
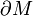 le bord de M, muni de l'orientation sortante, et
le bord de M, muni de l'orientation sortante, et  est l'inclusion canonique.
est l'inclusion canonique.Le théorème est attribué à Sir George Gabriel Stokes, mais le premier à connaître ce résultat est en réalité William Thomson. Le mathématicien et le physicien entretiennent une correspondance active durant 5 ans de 1847 à 1853.[1]
La preuve demande de disposer d'une bonne définition de l'intégration ; il faut se rendre compte que l'apparente simplicité de la démonstration actuelle est trompeuse.
Sommaire
Démonstration
L'idée est d'utiliser une partition de l'unité adaptée au problème dans la définition de l'intégrale d'une forme différentielle ; et de se ramener à un cas presque évident.
Soit {Ui}I un recouvrement localement fini de M par des domaines de cartes locales
 , telles que :
, telles que :Introduisons fi une partition de l'unité subordonnée à {Ui}. Comme le support de ω est fermé, la forme différentielle ω s'écrit :
où la sommation est à support fini. Posons
![\beta_i=\phi_i^*\left[f_i\omega\right]](/pictures/frwiki/48/0e09353643688c43fff332f6cfc42c37.png) , forme différentielle à support compact de
, forme différentielle à support compact de  . La restriction
. La restriction  est un difféomorphisme sur son image préservant les orientations sortantes. On a donc :
est un difféomorphisme sur son image préservant les orientations sortantes. On a donc :Comme
 commute avec l'opérateur de différentiation d, on a :
commute avec l'opérateur de différentiation d, on a :Par sommation, le théorème de Stokes est démontré une fois établi le cas particulier
 .
.Une (n-1)-forme ω sur
 s'écrit :
s'écrit :où le chapeau désigne une omission. On trouve alors :
Le théorème de Fubini donne :
L'hypothèse que la forme ω est à support compact permet alors de finir le calcul, car les termes
 pour
pour  sont tous nuls :
sont tous nuls :D'où le résultat.
Théorème fondamental de l'intégration
Si f est une fonction
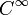 de la variable réelle, alors f est une forme différentielle de degré zéro, dont la différentielle est
de la variable réelle, alors f est une forme différentielle de degré zéro, dont la différentielle est  . Le bord orienté de [a,b] est {b} − {a} (extrémité avec l'orientation + et origine avec l'orientation -), quelles que soient les valeurs relatives de a et b. La formule de Stokes donne dans cette situation :
. Le bord orienté de [a,b] est {b} − {a} (extrémité avec l'orientation + et origine avec l'orientation -), quelles que soient les valeurs relatives de a et b. La formule de Stokes donne dans cette situation :En fait, le théorème de Stokes est la généralisation de cette formule aux dimensions supérieures. La difficulté se trouve bien davantage dans la mise en place du bon cadre (formes différentielles, variétés à bord ou éventuellement plus générales, orientations) que dans la démonstration, qui repose sur le théorème fondamental de l'intégration et un argument de partition de l'unité.
Formule de Green-Riemann
Article détaillé : théorème de Green.Soit U un domaine compact lisse de
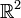 et
et  une 1-forme différentielle sur
une 1-forme différentielle sur 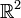 . Alors, la formule de Stokes s'écrit :
. Alors, la formule de Stokes s'écrit :La formule de Green-Riemann est utilisée en géométrie pour démontrer l'inégalité de Poincaré.
Formule d'Ostrogradsky
Article détaillé : théorème de Green-Ostrogradsky.Soit U un domaine compact à bord lisse de
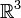 , et posons
, et posons  . Si X est un champ de vecteurs au voisinage de l'adhérence de U, alors sa divergence vérifie :
. Si X est un champ de vecteurs au voisinage de l'adhérence de U, alors sa divergence vérifie :La formule de Stokes donne alors :
Sens physique de la formule de Stokes
Notons
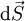 le champ de vecteurs normal sortant d'un domaine U relativement compact à bord régulier. Soit X un champ de vecteurs défini au voisinage de l'adhérence de D. On définit la forme surfacique sur
le champ de vecteurs normal sortant d'un domaine U relativement compact à bord régulier. Soit X un champ de vecteurs défini au voisinage de l'adhérence de D. On définit la forme surfacique sur  par :
par :On définit le flux de X par :
La formule d'Ostrogradsky se réécrit alors :
Soit
 , une courbe fermée orientée dans
, une courbe fermée orientée dans 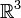 , S une surface orientée dont le contour est
, S une surface orientée dont le contour est  . L'orientation de
. L'orientation de  est induite par l'orientation de S. Si le champ vectoriel
est induite par l'orientation de S. Si le champ vectoriel 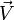 admet des dérivées partielles continues, alors :
admet des dérivées partielles continues, alors :où
 est le vecteur directeur de la courbe en tout point,
est le vecteur directeur de la courbe en tout point,  le rotationnel de
le rotationnel de 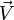 , et
, et 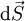 le vecteur normal à un élément de surface infinitésimal dont la norme est égale à la surface de l'élément.
le vecteur normal à un élément de surface infinitésimal dont la norme est égale à la surface de l'élément.Son application directe est le théorème d'Ampère (on l'applique au champ magnétique).
Application à l'homologie
La formule de Stokes est utilisée pour démontrer le théorème de dualité de De Rham.
La formule de Stokes permet aussi de démontrer le lemme de Poincaré. Ce dernier s'avère d'une grande utilité pour comprendre les isotopies en homologie. Il est aussi utilisé notablement dans la preuve du théorème de Darboux en géométrie symplectique.
Références
- ↑ (en) David B. Wilson, The Correspondence between Sir George Gabriel Stokes and Sir William Thomson, Baron Kelvin of Largs [détail des éditions]
- Portail de la géométrie
- Portail de la physique
Catégories : Théorème de mathématiques | Théorème de physique | Forme différentielle | Équations de Navier-Stokes
Wikimedia Foundation. 2010.






![\int_{\partial M}\!\left[f_i\omega\right]=\int_{\partial M'}\! \beta_i](/pictures/frwiki/101/e16091ed5c99ef3406320172fa7fceeb.png)
![\int_M\! \mathrm d\left[f_i\omega\right]=\int_{M'}\! \mathrm \mathrm d\beta_i](/pictures/frwiki/97/a000b57259b9d3555b59d982207733af.png)





![\int_{\partial U} \alpha = \int_{\partial U}\! \left[f\cdot \mathrm dx+g\cdot \mathrm dy\right]=\iint_U \left[\frac{\partial g}{\partial x} -\frac{\partial f}{\partial y}\right] \,\mathrm dx\,\mathrm dy](/pictures/frwiki/53/582d7002d0afb5e6f621b80297956397.png)
![\mathrm d\left[\iota_X\omega\right]=\mathrm{div}(X)\cdot\omega](/pictures/frwiki/49/180a7237afb65cd7998a2000a2e9546a.png)
![\int_{\partial U}\! \left[f\cdot \mathrm dy\wedge \mathrm dz+g\cdot \mathrm dz\wedge \mathrm dx+h\cdot \mathrm dx\wedge \mathrm dy\right]=\iiint_U\! \left[\frac{\partial f}{\partial x}+\frac{\partial g}{\partial y}+\frac{\partial h}{\partial z}\right]\, \mathrm dx\,\mathrm dy\,\mathrm dz](/pictures/frwiki/97/ad1716607f29931a257b4c8d3d36f9c1.png)



