Theoreme fondamental de l'analyse

Le théorème fondamental de l'analyse (ou théorème fondamental du calcul différentiel et intégral) déclare que les deux opérations de base de l'analyse, la dérivation et l'intégration, sont réciproques l'une de l'autre.

Ceci signifie que si une fonction continue est d'abord intégrée et ensuite dérivée, alors la fonction initiale est retrouvée.

Une conséquence importante de ce théorème, appelée parfois le deuxième théorème fondamental du calcul différentiel et intégral est de permettre de calculer une intégrale en utilisant une primitive de la fonction à intégrer.

Sommaire 1 Explication intuitive 2 Écriture formelle du théorème 2.1 Première partie 2.2 Seconde partie 3 Généralisations 4 Voir aussi 5 Référence

Explication intuitive

Intuitivement, le théorème dit simplement que si vous connaissez tous les petits changements instantanés d'une certaine quantité, alors vous pouvez calculer le changement général de cette quantité en additionnant tous les petits changements.

Pour se donner une idée de cette affirmation, commençons par donner un exemple. Supposons que nous voyagions sur une ligne droite, et que nous partions à l'instant t = 0, et avec une vitesse variable. Si 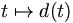indique notre distance à l'origine et 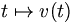représente notre vitesse à l'instant t, alors v(t) est le taux d'accroissement « infinitésimal » de d et est la valeur de la dérivée de d en t. Supposez que nous n'ayons qu'un compteur de vitesse qui indique la vitesse v(t), et que nous voulions retrouver notre distance d(t). Le théorème fondamental de l'analyse dit que nous devons primitiver v afin d'obtenir d. Et ceci est exactement ce que nous aurions fait, même sans connaître ce théorème : enregistrer la vitesse à des intervalles réguliers, peut-être toutes les minutes, et alors multiplier la première vitesse par 1 minute pour obtenir une estimation de la distance parcourue dans la première minute, puis multiplier la deuxième vitesse par 1 minute pour obtenir la distance parcourue dans la deuxième minute etc., et enfin ajouter toutes les distances précédentes. Pour obtenir une même meilleure estimation de notre distance actuelle, nous avons besoin d'enregistrer les vitesses à des intervalles de temps plus courts. La limite quand la longueur des intervalles tend vers zéro est exactement la définition de l'intégrale de v.

Écriture formelle du théorème

Première partie

Le théorème affirme que si la fonction f est continue sur un segment [a,b], alors la fonction F définie sur [a,b] par

.

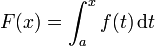est dérivable sur l'intervalle et sa dérivée est égale à f. Ici, t est une variable muette qui est seulement utilisée dans le but de l'opération d'intégration. De plus, si G est une fonction dérivable sur [a,b] telle que G'(x) = f(x), alors la fonction F − G est constante.

Voici une démonstration du théorème ci-dessus. Soit x₀ un réel de I, h un réel non nul et 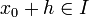. D'après la relation de Chasles :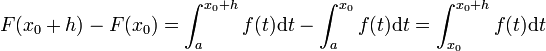

• Si h > 0, appelons m_h et M_h la borne supérieure et la borne inférieure de f(t) sur l'intervalle [x₀;x₀ + h]. D'après l'inégalité de la moyenne, on a

,

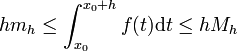ou encore

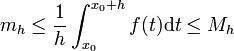
On applique le théorème des valeurs intermédiaires à f qui est continue et atteint ses bornes m_h et M_h sur [x₀;x₀ + h] : f prend n'importe quelle valeur comprise entre m_h et M_h, en particulier f atteint le réel de l'encadrement précédent. On a ainsi l'existence de tel que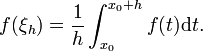

Or,

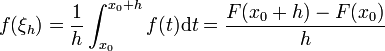
Quand h tend vers zéro, ξ_h tend vers x₀, et en vertu de la continuité de f, f(ξ_h) tend vers f(x₀).

• Si h < 0, on procède de même en faisant attention aux signes.

• Pour montrer la dernière partie, il suffit de voir qu'une fonction continue à dérivée nulle sur un intervalle est constante : on applique à la fonction le théorème des accroissements finis, pour n'importe quel sous-intervalle de l'intervalle de définition.

Remarque. Si on suppose f monotone, la démonstration se simplifie. Par exemple, si f est croissante et h > 0, on a m_h = f(x₀) et M_h = f(x₀ + h).

Seconde partie

La partie Ⅱ du théorème donne la principale méthode pour calculer l'intégrale de la fonction continue f : si F est une primitive quelconque de la fonction f (c.-à-d. si F vérifie ), alors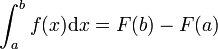

Comme exemple, supposons que nous ayons à calculer

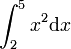
Ainsi, f(x) = x² et nous pouvons utiliser F définie par F(x) = x³ / 3 comme primitive. On a :

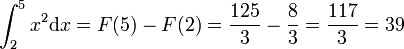
Ceci est la méthode inventée par Leibniz et Newton.

Généralisations

Le théorème fondamental de l'analyse s'étend aux fonctions non continues de la façon suivante :

• Si f est une fonction intégrable au sens de Lebesgue sur [a,b] et si x₀ est un point de Lebesgue de f (c'est en particulier le cas si f est continue en x₀), alors F définie sur [a,b] par 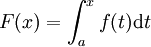est dérivable en x = x₀ et vérifie 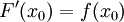. Cette relation est vérifiée presque partout.

• Si F est une fonction dérivable de dérivée intégrable au sens de Lebesgue, alors 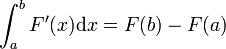. On peut même ne pas supposer F' intégrable, à condition d'utiliser l'intégrale de Kurzweil-Henstock. Il ne suffit pas qu'une fonction F soit dérivable presque partout pour que l'égalité soit vraie, comme le montre le contre-exemple de l'escalier de Cantor, mais l'égalité est vérifiée si on suppose que F est absolument continue.

La formule de Taylor avec reste intégral qui exprime le terme d'erreur comme une intégrale peut être vue comme une généralisation du théorème fondamental.

Il existe une version du théorème pour les fonctions de la variable complexe. Supposons que U soit une partie ouverte de et que 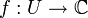admette une primitive F qui soit une fonction holomorphe sur U. Alors pour toute courbe , l'intégrale sur cette courbe peut être obtenue par :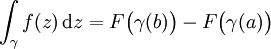

Le théorème fondamental peut être généralisé à des intégrales sur des contours ou sur des surfaces dans des dimensions supérieures et sur des espaces vectoriels (voir le théorème de Stokes).

Voir aussi

• Absolue continuité
• Escalier de Cantor
• Point de Lebesgue
• Théorème de différenciation de Lebesgue

Référence

Walter Rudin, Analyse réelle et complexe : cours et exercices [détail des éditions]

• Portail des mathématiques