Théorème Optimisation/Séparation
- Théorème Optimisation/Séparation
-
Théorème optimisation/séparation
Wikimedia Foundation.
2010.
Contenu soumis à la licence CC-BY-SA. Source : Article Théorème Optimisation/Séparation de Wikipédia en français (auteurs)
Regardez d'autres dictionnaires:
Theoreme optimisation/separation — Théorème optimisation/séparation Le théorème Optimisation/Séparation est une conséquence de la méthode de l ellipsoïde. Il constitue un résultat (très difficile à montrer) majeur en optimisation combinatoire qui fait le lien entre l approche… … Wikipédia en Français
Théorème Optimisation/Separation — Théorème optimisation/séparation Le théorème Optimisation/Séparation est une conséquence de la méthode de l ellipsoïde. Il constitue un résultat (très difficile à montrer) majeur en optimisation combinatoire qui fait le lien entre l approche… … Wikipédia en Français
Théorème optimisation/séparation — Le théorème Optimisation/Séparation est une conséquence de la méthode de l ellipsoïde. Il constitue un résultat (très difficile à montrer) majeur en optimisation combinatoire qui fait le lien entre l approche polyèdrale et l algorithmique. Ce… … Wikipédia en Français
Separation des convexes — Séparation des convexes Un exemple de séparation stricte Étant donnés deux convexes d un même plan ne se rencontrant pas, il est toujours possible de subdiviser le plan en deux demi plans de sorte que chacun contienne entièrement l un des… … Wikipédia en Français
Theoreme de projection sur un convexe ferme — Théorème de projection sur un convexe fermé En mathématiques, le théorème de projection orthogonale sur un convexe est un résultat de minimisation de la distance qui généralise la projection orthogonale sur un espace vectoriel. Il remplace… … Wikipédia en Français
Théorème de projection orthogonale sur un convexe — Théorème de projection sur un convexe fermé En mathématiques, le théorème de projection orthogonale sur un convexe est un résultat de minimisation de la distance qui généralise la projection orthogonale sur un espace vectoriel. Il remplace… … Wikipédia en Français
Theoreme de Hahn-Banach — Théorème de Hahn Banach Ce théorème, auquel a été donné le nom des deux mathématiciens Hans Hahn et Stefan Banach, garantit l existence d une forme linéaire vérifiant certaines conditions (valeurs imposées sur une partie de l espace, mais… … Wikipédia en Français
Théorème de hahn-banach — Ce théorème, auquel a été donné le nom des deux mathématiciens Hans Hahn et Stefan Banach, garantit l existence d une forme linéaire vérifiant certaines conditions (valeurs imposées sur une partie de l espace, mais limitées partout). En… … Wikipédia en Français
Théorème de Helly — dans le plan : si trois quelconques des convexes de la famille se rencontrent alors l intersection de tous ces convexes est non vide. Le théorème de Helly est un résultat combinatoire sur les convexes. Ce résultat a été prouvé en 1913 par… … Wikipédia en Français
Théorème de carathéodory (géométrie) — Le théorème de Carathéodory est un théorème de géométrie relatif aux enveloppes convexes dans le contexte des espaces affines de dimension finie. Sommaire 1 Énoncé 2 Preuves 2.1 La preuve usuelle … Wikipédia en Français
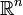 est constitué par l'ensemble des points
est constitué par l'ensemble des points 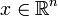 satisfaisant un nombre arbitrairement grand mais fini d'inégalités linéaires (i.e. de la forme
satisfaisant un nombre arbitrairement grand mais fini d'inégalités linéaires (i.e. de la forme 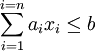 ).
).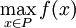 pour toute fonction linéaire f(x).
pour toute fonction linéaire f(x).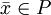 ou non, pour tout point
ou non, pour tout point 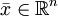 , et si non à déterminer un hyperplan séparant
, et si non à déterminer un hyperplan séparant 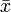 de P (i.e. trouver une inégalité linéaire violée par
de P (i.e. trouver une inégalité linéaire violée par 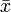 mais satisfaite par tout point de P).
mais satisfaite par tout point de P).