Théorème PBW

Théorème PBW: Théorème de Poincaré-Birkhoff-Witt

En mathématiques, et plus particulièrement dans la théorie des algèbres de Lie, le théorème de Poincaré-Birkhoff-Witt est un théorème fondamental qui permet de décrire précisément la structure de l'algèbre enveloppante d'une algèbre de Lie.

Énoncé

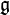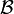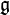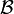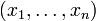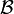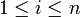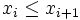Soit $\mathfrak{g}$ une algèbre de Lie, $\mathcal{B}$ une base de $\mathfrak{g}$ . On suppose que $\mathcal{B}$ est totalement ordonnée. On appelle monôme canonique toute suite finie $(x_1,\dots,x_n)$ d'éléments de $\mathcal{B}$ croissante au sens large (c'est-à-dire que pour tout $1\leq i \leq n$ , $x_i \leq x_{i+1}$ ).

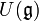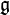La définition de l'algèbre enveloppante $U(\mathfrak{g})$ de $\mathfrak{g}$ assure l'existence d'une application linéaire
$L:\mathfrak{g} \longrightarrow U(\mathfrak{g})$
On étend $L$ aux monômes canoniques en posant
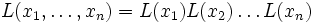
$L(x_1,\dots,x_n)=L(x_1)L(x_2)\dots L(x_n)$
ce qui a un sens puisque 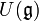$U(\mathfrak{g})$ est une algèbre associative.

Le théorème proprement dit est le suivant:

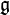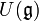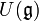L'application $L$ définit une injection de $\mathfrak{g}$ dans $U(\mathfrak{g})$ , et l'ensemble des images par $L$ des monômes canoniques est une base de $U(\mathfrak{g})$ .

Autrement dit, soit 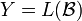$Y=L(\mathcal{B})$ . Alors l'ensemble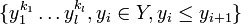
$\{ y_1^{k_1}\dots y_l^{k_l}, y_i \in Y, y_i \leq y_{i+1} \}$
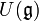est une base de $U(\mathfrak{g})$ .

Conséquence

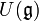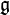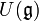L'application $L$ est injective. Ainsi, en munissant $U(\mathfrak{g})$ de sa structure naturelle d'algèbre de Lie (en posant $[x, y] = x y - y x$ ), $\mathfrak{g}$ peut être vue comme une sous-algèbre de Lie de $U(\mathfrak{g})$ .

Portail des mathématiques

Ce document provient de « Th%C3%A9or%C3%A8me de Poincar%C3%A9-Birkhoff-Witt ».

Catégorie : Algèbre de Lie

Contenu soumis à la licence CC-BY-SA. Source : Article Théorème PBW de Wikipédia en français (auteurs)

Игры ⚽ Нужна курсовая?

Regardez d'autres dictionnaires:

Algèbre enveloppante — Pour les articles homonymes, voir Algèbre (homonymie). En mathématiques, on peut construire l algèbre enveloppante d une algèbre de Lie . Il s agit une algèbre unitaire qui permet de rendre compte de la plupart des propriétés de … Wikipédia en Français

Dictionnaires et Encyclopédies sur 'Academic'

Théorème PBW

Théorème de Poincaré-Birkhoff-Witt

Énoncé

Conséquence

Regardez d'autres dictionnaires:

Share the article and excerpts

Dictionnaires et Encyclopédies sur 'Academic'

Wikipédia en Français

Théorème PBW

Théorème de Poincaré-Birkhoff-Witt

Énoncé

Conséquence

Regardez d'autres dictionnaires:

Share the article and excerpts

Direct link