- Théorie de galois inverse
-
Théorie de Galois inverse
En mathématiques et plus précisément en algèbre la Théorie de Galois inverse est une branche de la Théorie de Galois.
L'objet de la théorie est de répondre à la question : Soit G un groupe et K un corps, existe-t-il une extension de corps de K tel que son groupe de Galois soit G. Peut-on choisir L tel que l'extension soit galoisienne?
La plus grande conjecture de la théorie est la suivante Tout groupe fini est le groupe de Galois d'une extension galoisienne des nombres rationnels.
Malgré d'importants progrès durant les trente dernières années du XXe siècle et un grand nombre de résultats établis, la théorie reste une vaste conjecture en 2006.
Sommaire
Problématique
Le Théorème fondamental de la théorie de Galois montre que des extensions ayant même groupe de Galois sont très semblables. La détermination de ce groupe apprend enormément sur la structure de l'extension, elle est cependant souvent délicate. Il apparaît alors naturel de se poser la question inverse.
Les groupes de Galois des extensions algébriques sont naturellement munis d'une structure de groupe profini. On peut montrer réciproquement, par une construction ad hoc, que tout groupe profini G est bien groupe de Galois d'une certaine extension algébrique : soit F un corps (commutatif), on note K le corps des fractions rationnelles sur F en un ensemble d'indéterminées indicé par les éléments des groupes quotients de G par ses sous-groupes distingués ouverts. On peut alors montrer que l'extension K/KG est alors une extension galoisienne de groupe de Galois G. Cependant, rien n'assure que KG=F. Le problème de la théorie de Galois inverse devient : peut-on, via éventuellement une autre construction, obtenir KG=F ?
Cette question peut donc se résumer :
-
- Soit un groupe fini (ou profini) et un corps, existe-t-il une extension galoisienne de ce corps ayant pour groupe de Galois ce groupe?
- Soit un groupe fini (ou profini), existe-t-il une extension galoisienne des nombres rationnels ayant pour groupe de Galois ce groupe?
Aucune des questions n'est résolue en 2006.
Exemples
Groupe cyclique d'ordre deux
Considérons l'ensemble des rationnels de Gauss
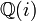. C'est une extension de Galois des nombres rationnels, de plus cette extension est de dimension deux. En conclusion son groupe de Galois est d'ordre deux et donc est le groupe cyclique d'ordre deux.D'ailleurs c'est le groupe de Galois de toute extension quadratique de Q. Soit le groupe de Galois associé à tout polynôme à coefficient rationnel irréductible de degré deux.
Groupe cyclique d'ordre p-1 avec p premier
Considérons l'extension
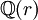où r est une racine primitive de l'unité. Cette extension est le corps de décomposition de r sur les nombres rationnels, elle est donc galoisienne et possède pour base l'ensemble des racines p ième de l'unité. Soit m un morphisme du groupe de Galois.Ce morphisme transforme toute racine p ième de l'unité en une racine p ième de l'unité, on en déduit l'existence d'un entier q non nul et strictement inférieur à p tel que m(r) = m(rq). Les propriétés de morphismes montre alors que m est totalement défini sur la base des racines car si n est un entier : m(r n) = m(r q.n). On en déduit que m est parfaitement défini sur une base, donc sur l'extension entière.
Réciproquement, si q est un entier strictement positif et strictement inféreieur à p, alors l'application de l'ensemble des racines p ièmes de l'unité dans lui-même définie par : r n → r q.n se prolonge clairement en un automorphisme du groupe de Galois.
On en déduit que l'extension possède comme groupe de Galois un groupe isomorphe à
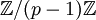. Le groupe est donc groupe de Galois d'une extension galoisienne des nombres rationnels.Quelques résultats
Les résultats suivants sont maintenant démontrés:
-
- Tout groupe abélien fini est le groupe de Galois du corps des nombres rationnels.
Il est même possible de choisir l'extension comme étant égale à une sous extension cyclotomique.
DémonstrationsSoit G un groupe abélien fini. Alors G est un produit de cycles et
![\exists (n_i)_{i\in [1,m]} \in \mathbb {N}^m \quad tel\; que\quad G \simeq \prod_{i=1}^m \mathbb{Z}/n_i\mathbb{Z}](/pictures/frwiki/56/8ab8655f635f98935fb60866eb969697.png)
Le théorème de Dirichlet assure de l'existence d'une infinité de nombres premiers distincts congrus à un modulo n, si n est un entier. On en déduit qu'il existe une famille d'entiers premiers (p i) tel que (Z/piZ*,.) contienne un sous-groupe isomorphe à Z/niZ. Ici (Z/piZ*,.) désigne le sous-groupe multiplicatif des éléments inversibles du corps. On en déduit l'existence d'un morphisme surjectif du groupe multiplicatif (Z/piZ*,.) dans le groupe additif Z/niZ.
Le Théorème chinois montre que si a et b sont deux nombres entiers premiers entre eux alors l'anneau Z/a Z x Z/b Z est isomorphe à l'anneau Z/ab Z. Ce théorème permet de montrer par récurrence que:
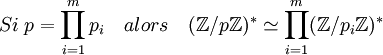
On en déduit donc l'existence d'un morphisme m surjectif de (Z/p Z*,.) dans G. Considérons alors l'extension cyclotomique L sur le corps des rationnels engendrée par les racines pième de l'unité. Son groupe de galois est isomorphe à (Z/p Z*,.). Le quotient du groupe de Galois par le noyau du morphisme (où (Z/p Z*,.) est identifié au groupe de Galois) est un groupe isomorphe à G. Le Théorème fondamental de la théorie de Galois nous indique aussi que c'est le groupe de Galois de l'extension galoisienne des éléments de L invariants par les actions du groupe noyau. Ce qui démontre la proposition.
-
- Tout groupe symétrique fini est le groupe de Galois d'une extension galoisienne du corps des rationnels.
- Tout groupe fini est le groupe de Galois d'une extension d'un corps de nombres.
- Tout groupe résoluble est le groupe de Galois d'une extension galoisienne du corps des rationnels. Ce résultat est dû à Igor Chafarevitch, dans une série de 4 articles parus en 1954. On peut en trouver une démonstration dans le livre de Neukirch, Schmidt et Wingberg.
Les différentes stratégies
Une méthode introduite par Hilbert
Pour un groupe G donné, l'idée de Hilbert est de réaliser ce groupe comme le groupe de Galois d'une extension de Q(T). Ensuite le théorème d'irréductibilité de Hilbert nous donne l'existence d'une infinité de valeurs rationnelles pour T pour lesquelles le groupe de Galois reste G[1].
Voir aussi
Notes
- ↑ Cette approche est développée dans le lien externe Théorie de Galois inverse et géométrie algébrique de Pierre Dèbes
Liens externes
- (fr) Un cours de DEA sur la théorie de Galois par Alain Kraus Université de Paris VI 1998
- (fr) Théorie de Galois inverse et géométrie algébrique Pierre Dèbes
- (fr) aspects élémentaires de la théorie de Galois inverse Colas Bardavid
Références
- Serge Lang, Algèbre, Dunod, 2004, 926 p. (ISBN 2100079808)[détail des éditions]
- (en) Jürgen Neukirch, Alexander Schmidt, Kay Wingberg Cohomology of number fields [détail des éditions]
- (en) Luis Ribes, Pavel Zalesskii, Profinite groups [détail des éditions]
- Pierre Samuel, Théorie algébrique des nombres [détail des éditions]
- E. Artin Galois Theory Notre Dame Press, Londres 1971
- B. Deschamps Problèmes d'arithmétique des corps et de théorie de Galois Hermann Paris 1998
Catégories : Théorie de Galois | Théorie -
Wikimedia Foundation. 2010.
