Théorie de galois à l'origine

Théorie de Galois à l'origine

Le travail de Galois proprement dit est fondé sur l'étude des « substitutions » des racines des polynômes appelées aujourd'hui permutations. Les permutations possibles sur une équation algébrique forment des groupes de permutations ; et en fait la notion abstraite de groupe fut introduite par Évariste Galois dans l'intention de décrire les permutations des racines.

Les travaux de Galois ont de multiples applications et permettent de résoudre des problèmes mathématiques classiques, comme par exemple :

quels sont les polygones qui peuvent être construits à la règle et au compas ?
pourquoi ne peut-on pas faire la trisection d'un angle ? (à nouveau d'une manière classique, à la règle et au compas) ;
et pourquoi n'y a-t-il pas de formule donnant les racines d'un polynôme de degré supérieur ou égal à cinq n'utilisant que les opérations algébriques usuelles et les racines nièmes ? (Théorème d'Abel-Ruffini.)

Qu'entendons-nous exactement par « substitutions des racines d'un polynôme » ? Une telle substitution est une permutation des racines telle qu'une équation algébrique satisfaite par les racines reste satisfaite après que les racines ont été permutées. Ces permutations forment un groupe appelé groupe de Galois. Selon l'ensemble dans lequel nous prenons les coefficients de l'équation algébrique, nous obtenons un groupe de Galois différent.

Par exemple, considérons le polynôme

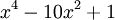
$x^4-10x^2+1\,$

qui peut aussi s'écrire

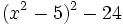$(x^2-5)^2-24\,$ ;

Nous voulons décrire le groupe de Galois de ce polynôme sur le corps des nombres rationnels (i.e. les équations algébriques vérifiées par les racines auront des nombres rationnels comme coefficients). Les racines de ce polynôme sont :

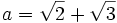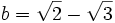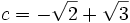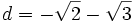$a = \sqrt{2} + \sqrt{3}\,$ , $b = \sqrt{2} - \sqrt{3}\,$ , $c = -\sqrt{2} + \sqrt{3}\,$ , $d = -\sqrt{2} - \sqrt{3}\,$ .

Il y a 24 façons possibles de permuter ces quatre nombres, mais toutes ces permutations ne sont pas éléments du groupe de Galois. Les permutations du groupe de Galois doivent préserver toute relation algébrique qui contient les variables a, b, c et d et les nombres rationnels. Une telle identité est par exemple a + d = 0.

Ainsi la permutation a→a, b→b, c→d et d→c ne convient pas, puisque a est envoyé sur a et d sur c, mais a + c n'est pas nul.

Un fait moins évident est que $(a + b)^2 = 8\,$ .

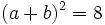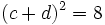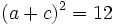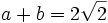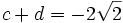Ainsi, nous pouvons envoyer (a, b) sur (c, d), puisque nous avons aussi $(c + d)^2 = 8\,$ , mais nous ne pouvons pas envoyer (a, b) sur (a, c) parce que $(a + c)^2 = 12\,$ . D'une autre façon, nous pouvons envoyer (a, b) sur (c, d), malgré le fait que $a + b = 2\sqrt{2}\,$ et $c + d = -2\sqrt{2}\,$ . C'est parce que l'identité 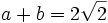$a + b = 2\sqrt{2}\,$ contient un nombre irrationnel, et ainsi nous n'avons pas besoin que les permutations du groupe de Galois la laissent invariante.

En résumé, nous obtenons que le groupe de Galois ne contient que les quatre permutations suivantes :

(a, b, c, d) → (a, b, c, d)

(a, b, c, d) → (c, d, a, b)

(a, b, c, d) → (b, a, d, c)

(a, b, c, d) → (d, c, b, a)

et le groupe de Galois est un groupe isomorphe au groupe de Klein.

Dans les approches modernes de la théorie de Galois, le formalisme a quelque peu changé, dans le but d'obtenir une définition plus précise et générale: on commence par définir la notion d'extension de corps L / K, puis son groupe de Galois comme le groupe de tous les automorphismes de corps de L qui laissent invariants tous les éléments de K. Dans l'exemple ci-dessus, nous avons déterminé le groupe de Galois de l'extension de corps $\mathbb Q$ (a,b,c,d) / $\mathbb Q$ .

La notion de groupe résoluble en théorie des groupes nous permet de déterminer si un polynôme est résoluble ou non par radicaux, selon que son groupe de Galois est résoluble ou non. Par essence même, chaque extension de corps L / K correspond à un groupe quotient dans une suite de composition du groupe de Galois. Si un groupe quotient dans la suite de composition est cyclique d'ordre n, alors l'extension de corps correspondante est une extension par radicaux, et les éléments de L peuvent être exprimés en utilisant la racine nième de certains éléments de K.

Si tous les groupes quotients dans sa suite de composition sont cycliques, alors le groupe de Galois est dit résoluble, et tous les éléments du corps correspondant peuvent être obtenus en prenant répétitivement un nombre fini de fois, des racines, produits, et sommes d'éléments du corps de base (habituellement $\mathbb Q$ ).

L'un des grands triomphes de la Théorie de Galois fut la preuve que pour tout n > 4, il existe des polynômes de degré n qui ne sont pas résolubles par radicaux. Ceci est dû au fait que pour n > 4 le groupe symétrique 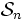$\mathcal{S}_n\,$ contient un sous-groupe distingué, simple, et non cyclique.

La théorie de Galois en détail

Préliminaires

Si $K$ est un corps, on appelle 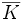$\overline K$ sa clôture algébrique. Pour une partie $A$ de 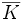$\overline K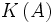$ on appelle $K\left(A\right)$ le plus petit sous-corps de 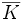$\overline K$ contenant $K$ et $A$ . On dira pour 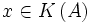$x\in K\left(A\right)$ que $x$ se déduit rationnellement de $A$ (parfois $K$ sera précisé, si ce n'est pas le cas ce sera souvent le corps engendré par les coefficient du polynôme).

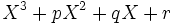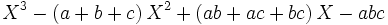Soit $P$ un polynôme. Par exemple $X^3+pX^2+qX+r\,$ . On remarquera que si l'on appelle ses trois racines $a\,$ , $b\,$ et $c\,$ . Alors ce polynôme s'écrit aussi $X^3-\left(a+b+c\right)X^2+\left(ab+ac+bc\right)X-abc$ . On remarquera que les coefficients s'expriment à l'aide de polynômes symétriques en les racines.

Théorème de l'élément primitif

Soit, $P\,$ , un polynôme irréductible. Si l'on prend un polynôme en ses racines tel qu'il décrive des valeurs différentes pour toutes les permutations de ses racines alors, si l'on appelle $V$ l'une de ces valeurs, chacune des racines du polynôme se déduit rationnellement de $V$ .

Preuve

L'existence du polynôme décrivant des valeurs différentes est à faire.

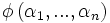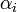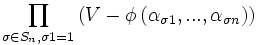Soit $n\,$ le degré du polynôme $P\,$ . On appelle $\phi\left(\alpha_1,...,\alpha_n\right)\,$ , où $\alpha_i\,$ sont les $n\,$ racines du polynôme $P\,$ . 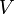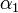L'expression $\prod_{\sigma\in S_n,\sigma1=1}\left(V-\phi\left(\alpha_{\sigma 1},...,\alpha_{\sigma n}\right)\right)\,$ , est invariante pour toutes les permutations des racines autres que la première et peut donc s'exprimer en un polynôme en $V\,$ et $\alpha_1\,$ , que l'on notera 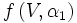$f\left(V,\alpha_1\right)\,$ . On remarque que le polynôme 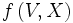$f\left(V,X\right)\,$ ne s'annule qu'en 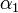$\alpha_1\,$ . 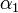En applicant l'algorithme d'Euclide pour trouver son $p g c d$ avec $P\,$ on obtiendra un polynôme du premier degré dont la racine est $\alpha_1\,$ . On peut donc exprimer 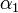$\alpha_1\,$ rationnellement en fonction de 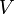$V\,$ . On fait de même avec les autres racines.

Q.E.D

Groupe du polynôme

Il existe un groupe de permutation des racines qui laisse toute quantité rationnellement connu invariable. Et tel que toute autre permutation des racines change ces quantités.

Preuve

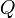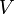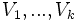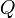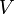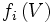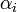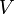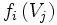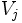Soit $Q\,$ le polynôme irréductible de $V\,$ . On appellera donc $V_1,...,V_k\,$ les racines de $Q\,$ . On a vu que chacune des racines de $P\,$ s'exprimait rationnellement en fonction de $V\,$ . Appelons $f_i\left(V\right)\,$ l'expression qui donne $\alpha_i\,$ en fonction de $V\,$ . On remarque que $f_i\left(V_j\right)\,$ est aussi une racine du polynôme $P\,$ . Ainsi pour chaque $V_j\,$ on a les racines du polynômes dans un certain ordre et pour un autre 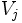$V_j\,$ dans un autre autre ordre. Toutes les permutations qui nous permettent de passer d'un ordre à l'autre est le groupe recherché.

Si l'on prend l'une de ces permutations cela va entraîner une permutation sur les 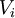$V_i\,$ et les quantités rationnellement connues étant les coefficients de 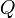$Q\,$ , permuter les 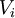$V_i\,$ ne changera pas les quantités rationnellement connues. Alors que faire une permutation en dehors de ce groupe va nous envoyer les 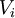$V_i\,$ sur des 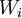$W_i\,$ , qui sont les racines d'un autre polynômes et donc les coefficients qui nous donnent les quantité connues vont être changés et les quantités connues aussi.

Q.E.D

Extension intermédiaire

Soit les différents ordres sur les racines. Si tous ces ordres se découpent en plusieurs groupes tels que toutes les permutations à l'intérieur de chacun de ces groupes soient les mêmes et si pour deux groupes ils existent une permutation qui les mettent en bijection (on remarquera qu'il s'agit en fait de sous-groupe distingué) alors ils existent une quantité invariante pour chacun de ces groupes et telles que l'on passe de l'une à l'autre par une permutation permettant de passer d'un groupe à l'autre. Alors ces quantités sont racines d'un même polynôme irréductible.

Réciproquement si l'on a une quantité qui s'exprime en les racines, alors chacun des groupes qui fixent l'un de ses conjugués sont tous les mêmes et deux de ces groupes sont en bijection grâce à une seule permutation.

Preuve

Il suffit de prendre encore une fois un polynôme en les racines tel qu'il soit invariant pour toutes les permutations à l'intérieur de l'un de ces groupes et variant pour toutes les autres. Le polynôme va avoir une valeur différente pour chaque groupe et comme l'on passe de l'une à l'autre grâce à toutes les permutations elles sont toutes conjuguées.

À mieux rédiger ce passage car important.

Liens externes

(fr) Mémoire sur les conditions de résolubilité des équations par radicaux (1830), texte de Galois et analyse sur le site BibNum.
[1] Les archives de Évariste Galois

Des notes de cours en anglais peuvent être consultées à :

http://www.galois-group.net/ en anglais

Portail des mathématiques

Ce document provient de « Th%C3%A9orie de Galois %C3%A0 l%27origine ».

Catégories : Théorie de Galois | Théorie

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Théorie de galois à l'origine de Wikipédia en français (auteurs)

Игры ⚽ Поможем сделать НИР

Regardez d'autres dictionnaires:

Theorie de Galois a l'origine — Théorie de Galois à l origine Le travail de Galois proprement dit est fondé sur l étude des « substitutions » des racines des polynômes appelées aujourd hui permutations. Les permutations possibles sur une équation algébrique forment… … Wikipédia en Français
Théorie de Galois à l'origine — Le travail de Galois proprement dit est fondé sur l étude des « substitutions » des racines des polynômes appelées aujourd hui permutations. Les permutations possibles sur une équation algébrique forment des groupes de… … Wikipédia en Français
Theorie de Galois — Théorie de Galois Évariste Galois 1811 1832 En mathématiques et plus précisément en algèbre, la théorie de Galois est l étude des extensions de corps commutatifs, par le biais d une correspondance avec des groupes de transformations sur ces… … Wikipédia en Français
Théorie de galois — Évariste Galois 1811 1832 En mathématiques et plus précisément en algèbre, la théorie de Galois est l étude des extensions de corps commutatifs, par le biais d une correspondance avec des groupes de transformations sur ces extensions, les groupes … Wikipédia en Français
Théorie de Galois — En mathématiques et plus précisément en algèbre, la théorie de Galois est l étude des extensions de corps commutatifs, par le biais d une correspondance avec des groupes de transformations sur ces extensions, les groupes de Galois. Cette méthode… … Wikipédia en Français
Theorie algebrique des nombres — Théorie algébrique des nombres En mathématiques, la théorie algébrique des nombres est la branche de l arithmétique utilisant des outils issus de l algèbre pour mieux comprendre les nombres. Son origine est l étude des nombres entiers et… … Wikipédia en Français
Théorie des équations (histoire des sciences) — Pour les articles homonymes, voir Théorie des équations. Évariste Galois offre une condition nécessaire et suffisante à la résolution d une équation polynomiale par l’algèbre. Il … Wikipédia en Français
Théorie algébrique des nombres — En mathématiques, la théorie algébrique des nombres est la branche de l arithmétique utilisant des outils issus de l algèbre pour mieux comprendre les nombres. Son origine est l étude des nombres entiers et particulièrement les équations… … Wikipédia en Français
Extension De Galois — En mathématiques, une extension de Galois (parfois nommée extension galoisienne) est une extension de corps finie normale séparable. L ensemble des automorphismes de l extension possède une structure de groupe appelé groupe de Galois. Cette… … Wikipédia en Français
Extension de galois — En mathématiques, une extension de Galois (parfois nommée extension galoisienne) est une extension de corps finie normale séparable. L ensemble des automorphismes de l extension possède une structure de groupe appelé groupe de Galois. Cette… … Wikipédia en Français

Dictionnaires et Encyclopédies sur 'Academic'

Théorie de galois à l'origine

Théorie de Galois à l'origine

Sommaire