Symbole de Levi-Civita

Le symbole de Levi-Civita, noté ε (lettre grecque epsilon), est un indicateur antisymétrique d'ordre 3 qui peut être exprimé à partir du symbole de Kronecker :

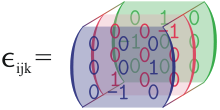
Visualisation d'un symbole de Levi-Civita en 3 dimensions.(i d'avant en arrière, j de haut en bas et k de gauche à droite)

$\varepsilon_{ijk} =\begin{vmatrix} \delta_{i1} & \delta_{i2}& \delta_{i3} \\ \delta_{j1} & \delta_{j2}& \delta_{j3} \\ \delta_{k1} & \delta_{k2}& \delta_{k3} \end{vmatrix}$

Ainsi $ε i j k$ ne peut prendre que trois valeurs : -1, 0 ou 1.

En 3 dimensions on peut figurer le symbole de Levi-Civita comme suit :

$\varepsilon_{ijk} = \begin{cases} +1 & \mbox{si } (i,j,k) \mbox{ est } (1,2,3), (2,3,1) \mbox{ ou } (3,1,2), \\ -1 & \mbox{si } (i,j,k) \mbox{ est } (3,2,1), (1,3,2) \mbox{ ou } (2,1,3), \\ 0 & \mbox{autrement: }i=j \mbox{ ou } j=k \mbox{ ou } k=i, \end{cases}$

La relation du symbole Levi-Civita au symbole de Kronecker:

ε i j k ε l m n = δ i l δ j m δ k n + δ i m δ j n δ k l + δ i n δ j l δ k m - δ i l δ j n δ k m - δ i n δ j m δ k l - δ i m δ j l δ k n

$\sum_{i=1}^3 \varepsilon_{ijk}\varepsilon_{imn} = \delta_{jm}\delta_{kn} - \delta_{jn}\delta_{km}$

$\sum_{i,j=1}^3 \varepsilon_{ijk}\varepsilon_{ijn} = 2\delta_{kn}$

On peut démontrer que:

$\sum_{i,j,k,\dots=1}^n \varepsilon_{ijk\dots}\varepsilon_{ijk\dots} = n!$

est vrai en n dimensions.

Interprétation

Dans une base orthonormée directe $\vec{e_1}, \vec{e_2}, \vec{e_3},$ ,
$ε i j k$ représente le volume orienté du parallépipède construit à partir des vecteurs $\vec{e_i}, \vec{e_j}, \vec{e_k},$ .

D'où une valeur égale à 0 si i=j, ou j=k, ou i=k.

Voir aussi

Portail des mathématiques

Catégories :

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Symbole de Levi-Civita de Wikipédia en français (auteurs)

Игры ⚽ Нужно решить контрольную?

Regardez d'autres dictionnaires:

Symbole de levi-civita — Le symbole de Levi Civita, noté ε (lettre grecque epsilon), est un indicateur antisymétrique d ordre 3 qui peut être exprimé à partir du symbole de Kronecker : Visualisation d un symbole de Levi Civita en 3 dimensions … Wikipédia en Français
Symbole de levi-civita d'ordre n — Sommaire 1 Définition 2 Exemple 3 Tenseur dualiseur 4 Formules // … Wikipédia en Français
Symbole de Levi-Civita d'ordre N — Sommaire 1 Définition 2 Exemple 3 Tenseur dualiseur 4 Formules Définition Le symbole de Levi Civita d ordre N, généralement noté … Wikipédia en Français
Tenseur de levi-civita — Articles scientifiques sur les tenseurs Généralités Tenseur Mathématiques Tenseur (mathématiques) Produit tensoriel ... de deux modules ... de deux applications linéaires Algèbre tensorielle Champ tensoriel Espace tensoriel … Wikipédia en Français
Tenseur de Levi-Civita — Le tenseur de Levi Civita – ou tenseur dualiseur – est un tenseur défini à partir du symbole de Levi Civita d ordre N . Étant donné un espace de dimension N, le symbole de Levi Civita d ordre N , aussi appelé pseudo tenseur unité complètement… … Wikipédia en Français
Tullio Levi-Civita — Naissance 29 mars 1873 Padoue ( … Wikipédia en Français
Tullio levi-civita — (29 mars 1873 à Padoue, Italie 29 décembre 1941 à Rome) est un mathématicien italien. Il est connu principalement pour son travail sur le calcul tensoriel et ses applications en théorie de la relativité. Il fut l assistant de Gregorio Ricci… … Wikipédia en Français
Symbole de Kronecker. — En mathématiques, le symbole de Kronecker est une fonction de deux variables qui est égale à 1 si celles ci sont égales, et 0 sinon. Il est symbolisé par la lettre δ (delta minuscule) de l alphabet grec, et est considéré comme une convention d… … Wikipédia en Français
Symbole de kronecker — En mathématiques, le symbole de Kronecker est une fonction de deux variables qui est égale à 1 si celles ci sont égales, et 0 sinon. Il est symbolisé par la lettre δ (delta minuscule) de l alphabet grec, et est considéré comme une convention d… … Wikipédia en Français
Symbole de Kronecker — En mathématiques, le symbole de Kronecker est une fonction de deux variables qui est égale à 1 si celles ci sont égales, et 0 sinon. Il est symbolisé par la lettre δ (delta minuscule) de l alphabet grec. Ou, en notation tensorielle : où δi… … Wikipédia en Français

Dictionnaires et Encyclopédies sur 'Academic'

Symbole de Levi-Civita

Interprétation

Voir aussi

Regardez d'autres dictionnaires:

Share the article and excerpts

Dictionnaires et Encyclopédies sur 'Academic'

Wikipédia en Français

Symbole de Levi-Civita

Interprétation

Voir aussi

Regardez d'autres dictionnaires:

Share the article and excerpts

Direct link