- Tenseur de Cotton
-
Tenseur de Cotton-York
GénéralitésMathématiquesTenseur (mathématiques)
Produit tensoriel
... de deux modules
... de deux applications linéaires
Algèbre tensorielle
Champ tensoriel
Espace tensorielPhysiqueConvention d'Einstein
Tenseur métrique
Tenseur énergie-impulsion
Tenseur de Riemann
... de Ricci
... d'Einstein
... de Weyl
... de Levi-Civita
... de Killing
... de Killing-Yano
... de Bel-Robinson
... de Cotton-York
Tenseur électromagnétique
Tenseur des contraintes
Tenseur des déformationsArticles connexesPortail des MathématiquesPortail de la PhysiqueEn géométrie riemannienne, le tenseur de Cotton-York ou tenseur de Cotton est un tenseur principalement utilisé dans les espaces tridimensionnels, car dans de tels espaces, il possède la propriété d'être nul si et seulement si l'espace est conformément plat.
Le tenseur de Cotton-York tire son nom des mathématiciens Émile Cotton et James W. York[1]. Certains résultats de Cotton ont été retrouvés indépendamment par York, ce qui justifie l'usage de l'une ou l'autre de ces appellations (Cotton et Cotton-York).
Sommaire
Formule
Le tenseur de Cotton-York s'écrit, en termes de composantes,
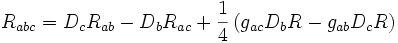 ,
,
où gab représente la métrique de l'espace considéré, R la courbure scalaire, Rab le tenseur de Ricci et D la dérivée covariante associée à la métrique.
Propriétés
Par construction, le tenseur de Cotton-York est antisymétrique par rapport à ses deux derniers indices et s'annule par sommation des permutations circulaires de ces indices :
- Rabc = − Racb,
- Rabc + Rbca + Rcab.
La contraction sur ses deux premiers indices est également nulle dans les espaces tridimensionnels :
- Raac = 0
DémonstrationCette contraction s'écrit, dans un espace à trois dimensions (où gab gab = 3)
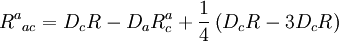 ,
,
ce qui donne
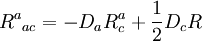 ,
,
qui est identiquement nul en raison de l'identité de Bianchi.
Nombre de composantes indépendantes
Le tenseur de Cotton-York possède a priori 27 composantes indépendantes ; l'antisymétrie sur les deux derniers indices réduit ce nombre à neuf, et la contraction sur les deux premiers induit trois contraintes supplémentaires, soit six composantes indépendantes. La contrainte sur les permutations circulaires introduit, toujours à trois dimensions, une contrainte supplémentaire, ce qui laisse au final cinq composantes indépendantes, soit seulement une de moins que le tenseur de Riemann qui, à trois dimensions, possède six composantes indépendantes.
Forme duale
Du fait de l'antisymétrie des deux dernières composantes du tenseur, on peut lui associer son tenseur dual au sens de la dualité de Hodge, défini par
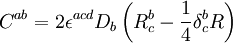 ,
,
où ε est le tenseur de Levi-Civita complètement antisymétrique par rapport à ses trois indices.
Certains auteurs réservent le nom de tenseur de Cotton à la première définition de Rabc et celle de tenseur de Cotton-York à celle ci-dessus.
Notes
- ↑ (fr) Émile Cotton, Sur les variétés à trois dimensions, Annales de la Faculté des Sciences de Toulouse II, 1, 385-438 (1899) Voir en ligne ; (en) James W. York, Gravitational Degrees of Freedom and the Initial-Value Problem, Physical Review Letters, 26, 1656-1658 (1972) Voir en ligne.
Références
- (en) D. Kramer, Hans Stephani, Malcolm Mac Callum & E. Herlt, Exact solutions of Einstein's field equations, Cambridge University Press, Cambridge, Angleterre, 1980, 428 pages (ISBN 0521230411), pages 55.
- Portail de la géométrie
- Portail de la physique
Catégorie : Géométrie riemannienne
Wikimedia Foundation. 2010.
