Contraction Du Symbole De Christoffel

Contraction Du Symbole De Christoffel: Contraction du symbole de Christoffel

La contraction du symbole de Christoffel s'exprime à partir de la dérivée partielle du déterminant du tenseur métrique.
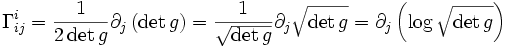
$\Gamma^i_{ij} = \frac{1}{2 \det{g}} \partial_j \left(\det g\right) = \frac{1}{\sqrt{\det{g}}} \partial_j \sqrt{\det{g}} = \partial_j \left(\log \sqrt{\det{g}}\right)$
Démonstration

Partant de l'expression du symbole de Christoffel en fonction de la dérivée partielle du tenseur métrique
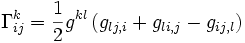$\Gamma^k_{ij} = \frac{1}{2} g^{kl} \left(g_{lj,i} + g_{li,j} - g_{ij,l}\right)$ ,
et profitant de la symétrie du tenseur métrique
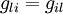
$g_{li} = g_{il}~$
on a
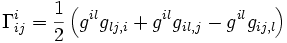$\Gamma^i_{ij} = \frac{1}{2} \left( g^{il} g_{lj,i} + g^{il} g_{il,j} - g^{il} g_{ij,l}\right)$ .
Échangeant $i$ et $l$ des produits internes du dernier terme, on voit que le premier terme le neutralise et l'on obtient
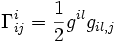$\Gamma^i_{ij} = \frac{1}{2} g^{il} g_{il,j}$ .
D'autre part la différentielle du déterminant $det g$ s'obtient en sommant le produit de chaque différentielle $d g i j$ d'un élément de matrice $g i j$ par le mineur correspondant à cet élément. Comme la matrice $g i j$ est l'inverse de la matrice du tenseur métrique $g i j$ , les mineurs cherchés sont $(det g) g i j$ . Ainsi $d(det g) = (det g) g i j d g i j$ et donc
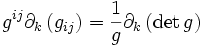
$g^{ij} \partial_k\left(g_{ij}\right) = \frac{1}{g} \partial_k \left(\det{g}\right)$
On a donc
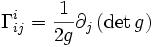$\Gamma^i_{ij} = \frac{1}{2 g} \partial_j \left(\det{g}\right)$ .
∎

Remarques

Le symbole de Christoffel étant symétrique, on a $Γ i i j = Γ i j i$

Ni le symbole de Christoffel ni la dérivée partielle ne représentent des tenseurs. Néanmoins cette formule peut figurer dans des expressions qui représentent des tenseurs.

Ce document provient de « Contraction du symbole de Christoffel ».

Catégories : Calcul tensoriel | Relativité générale | Géométrie riemannienne

Contenu soumis à la licence CC-BY-SA. Source : Article Contraction Du Symbole De Christoffel de Wikipédia en français (auteurs)

Игры ⚽ Нужна курсовая?

Regardez d'autres dictionnaires:

Contraction du symbole de christoffel — La contraction du symbole de Christoffel s exprime à partir de la dérivée partielle du déterminant du tenseur métrique. Démonstration Partant de l expression du symbole de Christoffel en fonction de la dérivée partielle du tenseur métrique … Wikipédia en Français
Contraction du symbole de Christoffel — La contraction du symbole de Christoffel s exprime à partir de la dérivée partielle du déterminant du tenseur métrique. Démonstration Partant de l expression du symbole de Christoffel en fonction de la dérivée partielle du tenseur métrique … Wikipédia en Français
Symbole de Christoffel — Symboles de Christoffel En mathématiques et en physique, les symboles de Christoffel, qui tirent leur nom du mathématicien Elwin Bruno Christoffel, sont une expression de la connexion de Levi Civita dérivée du tenseur métrique. Les symboles de… … Wikipédia en Français
Coefficients de Christoffel — Symboles de Christoffel En mathématiques et en physique, les symboles de Christoffel, qui tirent leur nom du mathématicien Elwin Bruno Christoffel, sont une expression de la connexion de Levi Civita dérivée du tenseur métrique. Les symboles de… … Wikipédia en Français
Symboles de christoffel — En mathématiques et en physique, les symboles de Christoffel, qui tirent leur nom du mathématicien Elwin Bruno Christoffel, sont une expression de la connexion de Levi Civita dérivée du tenseur métrique. Les symboles de Christoffel sont utilisés… … Wikipédia en Français
Symboles de Christoffel — En mathématiques et en physique, les symboles de Christoffel, qui tirent leur nom du mathématicien Elwin Bruno Christoffel, sont une expression de la connexion de Levi Civita dérivée du tenseur métrique. Les symboles de Christoffel sont utilisés… … Wikipédia en Français
Coefficients de connexion — Symboles de Christoffel En mathématiques et en physique, les symboles de Christoffel, qui tirent leur nom du mathématicien Elwin Bruno Christoffel, sont une expression de la connexion de Levi Civita dérivée du tenseur métrique. Les symboles de… … Wikipédia en Français
Tenseur de Levi-Civita — Le tenseur de Levi Civita – ou tenseur dualiseur – est un tenseur défini à partir du symbole de Levi Civita d ordre N . Étant donné un espace de dimension N, le symbole de Levi Civita d ordre N , aussi appelé pseudo tenseur unité complètement… … Wikipédia en Français
Tenseur de levi-civita — Articles scientifiques sur les tenseurs Généralités Tenseur Mathématiques Tenseur (mathématiques) Produit tensoriel ... de deux modules ... de deux applications linéaires Algèbre tensorielle Champ tensoriel Espace tensoriel … Wikipédia en Français
Tenseur dualiseur — Tenseur de Levi Civita Articles scientifiques sur les tenseurs Généralités Tenseur Mathématiques Tenseur (mathématiques) Produit tensoriel ... de deux modules ... de deux applications linéaires Algèbre tensorielle Champ tensoriel Espace tensoriel … Wikipédia en Français

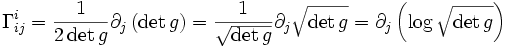
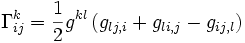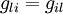
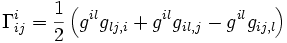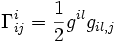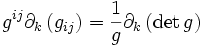
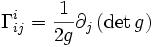Dictionnaires et Encyclopédies sur 'Academic'

Contraction Du Symbole De Christoffel

Contraction du symbole de Christoffel

Démonstration

Remarques

Regardez d'autres dictionnaires:

Share the article and excerpts

Dictionnaires et Encyclopédies sur 'Academic'

Wikipédia en Français

Contraction Du Symbole De Christoffel

Contraction du symbole de Christoffel

Démonstration

Remarques

Regardez d'autres dictionnaires:

Share the article and excerpts

Direct link