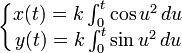Spirale de Fresnel

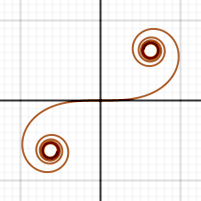
La clothoïde est une courbe transcendante plane dont la courbure est proportionnelle à l'abscisse curviligne.

Elle est également appelée spirale de Cornu, en référence à Alfred Cornu, le physicien français qui l'a inventée. Plus rarement, elle peut apparaître sous le nom de radioïde aux arcs, spirale d'Euler ou spirale de Fresnel.

Sommaire 1 Étymologie 2 Définition mathématique 3 Propriétés et applications 4 Voir aussi 5 Liens externes

Étymologie

Le mot clothoïde vient du grec klothein : filer (la laine), la forme de la courbe rappelant celle du fil qui s'enroule autour du métier à tisser. La même racine apparaît dans le nom de Clotho, celle des trois Parques qui tient le fil des destinées humaines.

Définition mathématique

La courbe peut être définie paramétriquement par l'équation suivante :

On voit que l'intégrale de Fresnel entre en jeu dans son calcul.

On peut également la définir par une équation intrinsèque :

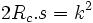, où R_c représente le rayon de courbure et s l'abscisse curviligne.

Propriétés et applications

En cinématique, la propriété fondamentale de la clothoïde se traduit par « une trajectoire qui, parcourue à vitesse constante, est telle que sa courbure varie linéairement ». La force centrifuge subie par un observateur circulant de façon continue le long de cette courbe varie donc continûment.

Concrètement, elle représente la trajectoire d'une automobile se déplaçant à vitesse stabilisée et dont on tourne le volant progressivement. C'est donc la trajectoire la plus « confortable », celle que l'on adopte pour le tracé des autoroutes. En pratique, on n'utilise cette courbe que pour assurer le raccordement progressif d'un alignement droit et d'un arc de cercle. Pour plus d'information, on se reportera à l'article sur le tracé en plan d'une route.

Pour les mêmes raisons, on utilise la clothoïde aux fins de courbes dans les tracés des chemins de fer parce qu'un véhicule suivant ce tracé à une vitesse constante subit une accélération angulaire constante, ce qui réduit à la fois les efforts sur les rails et l'inconfort des passagers dans les voitures. On retrouve cette courbe dans les boucles verticales ou loopings des montagnes russes pour le confort des passagers, afin que l'accélération verticale subie soit continue.

Enfin, les sabots montés sur les pylones de téléphériques, et qui supportent le cable porteur, adoptent cette forme. De fait, il est possible de faire circuler la cabine à sa vitesse maximale sur le pylone, sans incommoder les passagers.

Hors ces aspects cinématiques, la clothoïde intervient en sidérurgie pour aplanir ou ou plier les tôles et barres de grande épaisseur (au-delà de 30 mm). On limite ainsi le risque d'apparition de criques tout en ménageant le matériel. Typiquement, les outils concernés sont la coulée continue et les cintreuses.

D'autre part, une fois la clothoïde tracée, on peut en déduire des valeurs approchées d'expressions intervenant dans le calcul de la vibration résultante lors des phénomènes de diffraction. C'est la raison de l'utilisation de cette courbe par le physicien Alfred Cornu. Néanmoins, les moyens de calcul actuels l'ont fait tomber en désuétude pour cet usage.

Voir aussi

L'anti-clothoïde, plus couramment appelée développante du cercle, est la courbe que trace la main quand elle déroule une bobine de fil. Elle est utilisée dans la conception de profils d'engrenages.

Liens externes

• Description mathématique de la Spirale de Cornu
• Sur le site Mathcurve.com
• La Spirale de Cornu et les chemins de fer

Exemples de courbes
Coniques (cercle, ellipse, parabole, hyperbole)
Cardioïde • Cissoïde • Clothoïde • Cycloïde • Épicycloïde • Folium de Descartes • Hélice • Hypocycloïde (astroïde, deltoïde) • Hypotrochoïde • Spirale (d'Archimède, logarithmique)
Lemniscates (lemniscate de Gerono, lemniscate de Booth, lemniscate de Bernoulli, courbe du diable)
Trajectoire • Ovale de Cassini • Chaînette • Courbe brachistochrone

• Portail de la géométrie